In diesem Thema
R-Qd der Abweichung
Das R2 der Abweichung wird im Allgemeinen als Anteil der Gesamtabweichung der Antwortvariablen angesehen, der vom Modell erklärt wird.
Interpretation
Je höher das R2 der Abweichung ausfällt, desto besser ist das Modell an die Daten angepasst. Das R2 der Abweichung liegt immer zwischen 0 % und 100 %.
Das R2 der Abweichung nimmt beim Einbinden zusätzlicher Terme in ein Modell stets zu. Das beste Modell mit fünf Termen weist beispielsweise immer ein R2 auf, das mindestens so hoch wie das des besten Modells mit vier Termen ist. Daher ist das R2 der Abweichung am nützlichsten, wenn Sie Modelle derselben Größe vergleichen.
Statistiken für die Güte der Anpassung sind nur eines der Maße für die Güte der Anpassung des Modells an die Daten. Selbst wenn ein Modell einen erwünschten Wert aufweist, sollten Sie die Residuendiagramme und die Tests auf Güte der Anpassung untersuchen, um zu beurteilen, wie gut das Modell an die Daten angepasst ist.
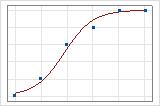
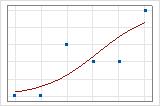
Sie können eine Darstellung der Anpassungslinie verwenden, um verschiedene Werte des R2 der Abweichung grafisch zu veranschaulichen. Das erste Diagramm zeigt ein Modell, das ungefähr 96 % der Abweichung in der Antwortvariablen erklärt. Das zweite Diagramm zeigt ein Modell, das ungefähr 60 % der Abweichung in der Antwortvariablen erklärt. Je mehr der Abweichung durch das Modell erklärt wird, desto näher liegen die Datenpunkte an der Kurve. Würde ein Modell theoretisch 100 % der Abweichung erklären, wären die angepassten Werte immer gleich den beobachteten Werten, und alle Datenpunkte würden auf der Kurve liegen.
Die Anordnung der Daten beeinflusst den Wert des R2 der Abweichung. Das R2 der Abweichung ist im Allgemeinen für Daten mit mehreren Versuchen pro Zeile höher als für Daten mit einem einzigen Versuch pro Zeile. Werte des R2 der Abweichung sind nur bei Modellen vergleichbar, in denen dasselbe Datenformat verwendet wird. Weitere Informationen finden Sie unter Wie wirken sich Datenformate bei der binären logistischen Regression auf die Güte der Anpassung aus?.
R-Qd (kor) der Abweichung
Das korrigierte R2 der Abweichung ist der Anteil der Abweichung der Antwortvariablen, der durch das Modell erklärt wird, korrigiert nach der Anzahl der Prädiktoren im Modell in Bezug auf die Anzahl der Beobachtungen.
Interpretation
Verwenden Sie das korrigierte R2 der Abweichung, wenn Sie Modelle vergleichen möchten, die eine unterschiedliche Anzahl von Termen enthalten. Das R2 der Abweichung nimmt beim Einbinden eines Terms in das Modell stets zu. Der Wert des korrigierten R2 der Abweichung berücksichtigt die Anzahl der Terme im Modell, was die Auswahl des richtigen Modells erleichtert.
| Treppenförmig | %Kartoffel | Abkühlgeschwindigkeit | Frittiertemperatur | R2 der Abweichung | Korrigiertes R2 der Abweichung | p-Wert |
|---|---|---|---|---|---|---|
| 1 | X | 0,000 | ||||
| 1 | X | X | 63 | 0,000 | ||
| 3 | X | X | X | 65 | = | 0,000 |
Der erste Schritt ergibt ein statistisch signifikantes Regressionsmodell. Im zweiten Schritt wird dem Modell die Abkühlgeschwindigkeit hinzugefügt; dadurch nimmt das korrigierte R2 der Abweichung zu, was darauf hinweist, dass die Abkühlgeschwindigkeit das Modell verbessert. Im dritten Schritt, in dem die Frittiertemperatur zum Modell hinzugefügt wird, nimmt das R2 der Abweichung, nicht aber das korrigierte R2 der Abweichung zu. Diese Ergebnisse deuten darauf hin, dass das Modell durch „Frittiertemperatur“ nicht verbessert wird. Auf der Grundlage dieser Ergebnisse erwägen Sie, „Frittiertemperatur“ aus dem Modell zu entfernen.
Die Anordnung der Daten beeinflusst den Wert des korrigierten R2 der Abweichung. Bei den gleichen Daten ist das korrigierte R2 der Abweichung im Allgemeinen für Daten mit mehreren Versuchen pro Zeile höher als für Daten mit einem einzigen Versuch pro Zeile. Verwenden Sie das korrigierte R2 der Abweichung nur zum Vergleichen der Anpassung von Modellen, die dasselbe Datenformat aufweisen. Weitere Informationen finden Sie unter Wie wirken sich Datenformate bei der binären logistischen Regression auf die Güte der Anpassung aus?.
R-Qd der Abweichung für Test
Interpretation
Verwenden Sie das R2 der Abweichung für den Test, um zu bestimmen, wie gut Ihr Modell für neue Daten passend ist. Modelle mit einem größeren R2 der Abweichung für den Test haben bei neuen Daten eine tendenziell bessere Leistung. Sie können das R2 der Abweichung für den Test verwenden, um die Leistung verschiedener Modelle zu vergleichen.
Ein R2 der Abweichung für den Test, das wesentlich kleiner als das R2 der Abweichung ist, kann auf eine übermäßige Anpassung des Modells hinweisen. Ein Modell ist übermäßig angepasst, wenn Sie Terme für Effekte hinzufügen, die in der Grundgesamtheit nicht wichtig sind. Das Modell wird auf die Trainingsdaten zugeschnitten und ist daher möglicherweise nicht nützlich, um Prognosen zur Grundgesamtheit zu treffen.
Angenommen, ein Analyst bei einem Finanzberatungsunternehmen entwickelt ein Modell, um zukünftige Marktbedingungen zu prognostizieren. Das Modell sieht vielversprechend aus, weil es ein R2 von 87 % aufweist. Das R2 der Abweichung für den Test beträgt jedoch 52 %, was auf eine übermäßige Anpassung des Modells hinweist.
Ein hohes R2 der Abweichung für den Test allein weist nicht darauf hin, dass das Modell die Modellannahmen erfüllt. Sie sollten die Residuendiagramme untersuchen, um die Annahmen zu überprüfen.
R-Qd der Abweichung für K Faltungen
Das R2 der Abweichung für K Faltungen wird in der Regel als der Anteil der Gesamtabweichung in der Antwortvariablen der Validierungsdaten betrachtet, der durch das Modell erklärt wird.
Interpretation
Bestimmen Sie anhand des R2 der Abweichung für K Faltungen, wie gut Ihr Modell für neue Daten passend ist. Modelle mit einem größeren R2 der Abweichung für K Faltungen haben bei neuen Daten eine tendenziell bessere Leistung. Sie können das R2 der Abweichung für K Faltungen verwenden, um die Leistung verschiedener Modelle zu vergleichen.
Ein R2 der Abweichung für K Faltungen, das wesentlich kleiner als das R2 der Abweichung ist, kann auf eine übermäßige Anpassung des Modells hinweisen. Ein Modell ist übermäßig angepasst, wenn Sie Terme für Effekte hinzufügen, die in der Grundgesamtheit nicht wichtig sind. Das Modell wird auf den Trainingsdatensatz zugeschnitten und ist daher möglicherweise nicht nützlich, um Prognosen zur Grundgesamtheit zu treffen.
Ein Analytiker bei einem Finanzberatungsunternehmen entwickelt beispielsweise ein Modell zum Prognostizieren künftiger Marktbedingungen. Das Modell sieht vielversprechend aus, weil es ein R2 der Abweichung von 87 % aufweist. Das R2 der Abweichung für K Faltungen beträgt jedoch 52 %, was auf eine übermäßige Anpassung des Modells hinweist.
Ein hohes R2 der Abweichung für K Faltungen allein weist nicht darauf hin, dass das Modell die Modellannahmen erfüllt. Sie sollten die Residuendiagramme untersuchen, um die Annahmen zu überprüfen.
AIC, AICc und BIC
Akaikes Informationskriterium (AIC), Akaikes korrigiertes Informationskriterium (AICc) und das Bayessche Informationskriterium (BIC) sind Maße der relativen Qualität eines Modells, bei denen sowohl die Anpassung als auch die Anzahl der Terme im Modell berücksichtigt werden.
Interpretation
- AICc und AIC
- Wenn die Stichprobengröße im Verhältnis zur Anzahl der Parameter im Modell klein ist, erbringt das AICc eine bessere Leistung als das AIC. Das AICc erbringt deshalb eine bessere Leistung, weil das AIC bei kleinen Stichprobenumfängen für Modelle mit zu vielen Parametern tendenziell klein ist. In der Regel liefern die beiden Statistiken ähnliche Ergebnisse, wenn der Stichprobenumfang im Verhältnis zur Anzahl der Parameter im Modell hinreichend groß ist.
- AICc und BIC
- Sowohl das AICc als auch das BIC werten die Likelihood des Modells aus und wenden dann einen Abzug für das Hinzufügen von Termen zum Modell an. Durch den Abzug wird die Tendenz zur Überanpassung des Modells an die Stichprobendaten reduziert. Durch diese Reduzierung kann ein Modell zustande kommen, das insgesamt eine bessere Leistung erbringt.
Fläche unterhalb der ROC-Kurve
Die ROC-Kurve zeigt die Richtig-Positiv-Rate (TPR), auch als Trennschärfe bezeichnet, auf der y-Achse und die Falsch-Positiv-Rate (FPR), auch als Fehler 1. Art bezeichnet, auf der x-Achse. Die verschiedenen Punkte stellen unterschiedliche Schwellenwerte für die Wahrscheinlichkeit dar, dass ein Fall ein Ereignis ist. Die Fläche unter einer ROC-Kurve gibt an, ob das binäre Modell ein guter Klassifikator ist.
Wenn in der Analyse eine Validierungsmethode verwendet wird, berechnet Minitab zwei ROC-Kurven, eine für die Trainingsdaten und eine für die Validierungsdaten. Wenn es sich bei der Validierungsmethode um einen Testdatensatz handelt, zeigt Minitab die Fläche unter der ROC-Kurve für den Test an. Wenn es sich bei der Validierungsmethode um die Kreuzvalidierung handelt, zeigt Minitab die Fläche unter der ROC-Kurve für K Faltungen an. Für eine Kreuzvalidierung mit 10 Faltungen zeigt Minitab beispielsweise die Fläche unter der ROC-Kurve für 10 Faltungen an.
Interpretation
Die Fläche unter der ROC-Kurve nimmt typischerweise Werte von 0,5 bis 1 an. Wenn das binäre Modell die Klassen perfekt trennen kann, entspricht die Fläche unter der Kurve 1. Wenn das binäre Modell die Klassen nicht besser als eine zufällige Einteilung trennen kann, entspricht die Fläche unter der Kurve 0,5.
Wenn in der Analyse eine Validierungsmethode verwendet wird, verwenden Sie die Fläche unter der ROC-Kurve für die Validierungsmethode, um zu bestimmen, ob das Modell die Werte der Antwortvariablen für neue Beobachtungen angemessen prognostizieren oder die Beziehungen zwischen der Antwortvariablen und den Prädiktorvariablen richtig zusammenfassen kann. Die Ergebnisse für die Trainingsdaten sind in der Regel optimaler als für die tatsächlichen Daten und dienen nur zur Referenz.
Wenn die Fläche unter der ROC-Kurve für die Validierungsmethode wesentlich kleiner ist als die Fläche unter der ROC-Kurve ist, kann die Differenz darauf hinweisen, dass das Modell übermäßig angepasst ist. Ein Modell ist übermäßig angepasst, wenn das Modell Terme enthält, die in der Grundgesamtheit nicht wichtig sind. Das Modell wird auf die Trainingsdaten zugeschnitten und ist daher möglicherweise nicht nützlich, um Prognosen zur Grundgesamtheit zu treffen.
Zusammenfassung des Modells
| R-Qd der Abweichung | R-Qd(kor) der Abweichung | AIC | AICc | BIC | Fläche unter der ROC-Kurve | R-Qd der Abweichung für 10 Faltungen | Fläche unter der ROC-Kurve für 10 Faltungen |
|---|---|---|---|---|---|---|---|
| 50,86% | 42,43% | 276,02 | 286,11 | 409,48 | 0,9282 | 17,29% | 0,8519 |
Diese Ergebnisse zeigen die Tabelle mit der Zusammenfassung des Modells für ein übermäßig angepasstes Modell. Die Fläche unter der ROC-Kurve für die Trainingsdaten gibt einen optimistischeren Wert dafür an, wie gut das Modell für neue Daten passend ist, als die Fläche unter der ROC-Kurve für 10 Faltungen.
