In diesem Thema
Exponentialfamilie und Linkfunktionen
Die Erweiterung der klassischen linearen Modelle auf verallgemeinerte lineare Modelle umfasst zwei Teile: eine Verteilung aus der Exponentialfamilie und eine Linkfunktion.
Exponentialfamilie
Der erste Teil erweitert das lineare Modell auf Antwortvariablen, die zu einer großen Familie von Verteilungen gehören, die als Exponentialfamilie bezeichnet werden. Mitglieder der Exponentialfamilie von Verteilungen weisen Dichtefunktionen für einen beobachteten Wert der Antwortvariablen in dieser allgemeinen Form auf:
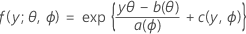
Hierbei gilt: a(∙), b(∙) und c(∙) hängen von der Verteilung der Antwortvariablen ab. Der Parameter θ ist ein Lageparameter, der oft als kanonischer Parameter bezeichnet wird, und ϕ wird als Streuungsparameter bezeichnet. Die Funktion a(ϕ) hat meistens die Form a(ϕ) = ϕ/ ω, wobei ω eine bekannte Konstante oder Gewichtung ist, die zwischen den Beobachtungen variieren kann. (Wenn in Minitab Gewichtungen angegeben werden, wird die Funktion a(ϕ) entsprechend korrigiert.)
Bei Mitgliedern der Exponentialfamilie kann es sich um diskrete Verteilungen oder stetige Verteilungen handeln. Beispiele für stetige Verteilungen, die zur Exponentialfamilie gehören, sind die Normalverteilung und die Gamma-Verteilung. Zu den diskreten Verteilungen, die zur Exponentialfamilie gehören, zählen zum Beispiel die Binomialverteilung und die Poisson-Verteilung. In der folgenden Tabelle werden die Merkmale einiger dieser Verteilungen aufgeführt.
| Verteilung | ϕ | b(θ) | a(φ) | c(y, ϕ) |
| Normal | σ2 | θ2/2 | φω |  |
| Binomial | 1 | 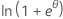 |
φ/ω | -ln(y!) |
| Poisson | 1 | exp(θ) | φ/ω |  |
Linkfunktion
Der zweite Teil ist die Linkfunktion. Die Linkfunktion setzt den Mittelwert der Antwortvariablen in der i-ten Beobachtung in folgender Form zu einem linearen Prädiktor in Beziehung:
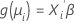
Das klassische lineare Modell ist ein Sonderfall dieser allgemeinen Formel, wobei die Linkfunktion die Identitätsfunktion ist.
Die Auswahl der Linkfunktion im zweiten Teil hängt von der spezifischen Verteilung der Exponentialfamilie im ersten Teil ab. Jede Verteilung in der Exponentialfamilie weist eine bestimmte Linkfunktion auf, die als kanonische Linkfunktion bezeichnet wird. Diese Linkfunktion erfüllt die Gleichung g (μi) = Xi'β = θ, wobei θ der kanonische Parameter ist. Die kanonische Linkfunktion ergibt einige erwünschte statistische Eigenschaften des Modells. Mit Hilfe der Statistiken für die Güte der Anpassung können Sie die Anpassungen mit den verschiedenen Linkfunktionen vergleichen. Bestimmte Linkfunktionen können aus historischen Gründen verwendet werden, oder weil sie eine bestimmte Bedeutung in einer Disziplin haben. Beispielsweise besteht ein Vorteil der Logit-Linkfunktion darin, dass sie einen Schätzwert für das Chancenverhältnis liefert. Ein weiteres Beispiel ist die Normit-Linkfunktion: Bei dieser wird angenommen, dass eine zugrunde liegende Variable vorhanden ist, die einer Normalverteilung folgt und in binäre Kategorien unterteilt ist.
Minitab bietet drei Linkfunktionen für jede Klasse von Modellen. Mit Hilfe der verschiedenen Linkfunktionen können Sie Modelle bestimmen, die bei unterschiedlich ausgeprägten Daten eine adäquate Anpassung bieten.
Bei Binomialmodellen lauten die Linkfunktionen: Logit, Normit (auch als Probit bezeichnet) und Gompit (auch als komplementärer Log-Log bezeichnet). Hierbei handelt es sich um die Umkehrung der regulären kumulativen logistischen Verteilungsfunktion (Logit), die Umkehrung der regulären kumulativen Normalverteilungsfunktion (Normit) und die Umkehrung der Gompertz-Verteilungsfunktion (Gompit). Die Logit-Linkfunktion ist die kanonische Linkfunktion für Binomialmodelle, und somit ist Logit die standardmäßig vorgegebene Linkfunktion.
Bei Poisson-Modellen lauten die Linkfunktionen: natürlicher Logarithmus, Quadratwurzel und Identität. Der natürliche Logarithmus ist die kanonische Linkfunktion für Poisson-Modelle und somit die standardmäßig vorgegebene Linkfunktion.
Die Linkfunktionen werden im Folgenden zusammengefasst:
| Modell | Name | Linkfunktion, g(μi) |
| Binomial | Logit | 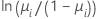 |
| Binomial | Normit (Probit) | 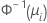 |
| Binomial | Gompit (komplementärer Log-Log) |  |
| Poisson | natürlicher Logarithmus | 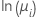 |
| Poisson | Quadratwurzel |  |
| Poisson | Identität | 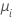 |
Notation
| Begriff | Beschreibung |
|---|---|
| μi | Mittelwert der Antwortvariablen in der i-ten Zeile |
| g(μi) | Linkfunktion |
| X | Vektor der Prädiktorvariablen |
| β | Vektor der Koeffizienten, die den Prädiktoren zugeordnet sind |
 | inverse kumulative Verteilungsfunktion der Normalverteilung |
Koeffizienten
[1] P. McCullagh und J. A. Nelder (1989). Generalized Linear Models, 2nd Ed., Chapman & Hall/CRC, London.
Standardfehler der Koeffizienten
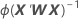
W ist eine Diagonalmatrix, bei der die Diagonalelemente mit der folgenden Formel angegeben werden:
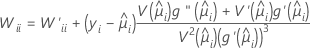
Dabei gilt Folgendes:

Diese Varianz-Kovarianz-Matrix beruht nicht auf der Fisher-Informationsmatrix, sondern auf der beobachteten Hesse-Matrix. Minitab verwendet die beobachtete Hesse-Matrix, da das resultierende Modell robuster gegenüber fehlerhaften Angaben der bedingten Mittelwerte ist.
Wenn die kanonische Linkfunktion verwendet wird, sind die beobachtete Hesse-Matrix und die Fisher-Informationsmatrix identisch.
Notation
| Begriff | Beschreibung |
|---|---|
| yi | Wert der Antwortvariablen für die i-te Zeile |
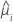 | geschätzter Mittelwert der Antwortvariablen für die i-te Zeile |
| V(·) | Varianzfunktion aus der folgenden Tabelle |
| g(·) | Linkfunktion |
| V '(·) | erste Ableitung der Varianzfunktion |
| g'(·) | erste Ableitung der Linkfunktion |
| g''(·) | zweite Ableitung der Linkfunktion |
Die Varianzfunktion hängt vom Modell ab:
| Modell | Varianzfunktion |
| Binomial | 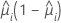 |
| Poisson | 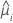 |
Weitere Informationen finden Sie unter [1] und [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh und J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Chancenverhältnisse für eine binäre logistische Regression
Das Chancenverhältnis wird nur ausgegeben, wenn Sie für ein Modell mit einer binären Antwortvariablen die Logit-Linkfunktion auswählen. In diesem Fall ist das Chancenverhältnis hilfreich beim Interpretieren der Beziehung zwischen einem Prädiktor und einer Antwortvariablen.
Der Wert für das Chancenverhältnis (τ) kann jede nicht negative Zahl sein. Das Chancenverhältnis = 1 dient als Basis für den Vergleich. Wenn τ = 1, besteht zwischen der Antwortvariablen und dem Prädiktor keine Assoziation. Wenn τ < 1, ist die Chance für das Ereignis auf der Referenzstufe des Faktors (oder auf niedrigeren Stufen eines stetigen Prädiktors) größer. Wenn τ > 1, ist die Chance für das Ereignis auf der Referenzstufe des Faktors (oder auf niedrigeren Stufen eines stetigen Prädiktors) kleiner. Je weiter ein Wert von 1 entfernt ist, desto stärker ist der Grad der Assoziation.
Hinweis
Für das binäre logistische Regressionsmodell mit einer Kovariate oder einem Faktor beträgt die geschätzte Erfolgschance:
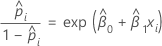
Die exponentielle Beziehung liefert eine Interpretation für β: Die Chance steigt bei jeder Zunahme von x um eine Einheit multiplikativ um eβ1. Das Chancenverhältnis entspricht exp(β1).
Wenn β z. B. 0,75 beträgt, beträgt das Chancenverhältnis exp(0,75), also 2,11. Dies weist darauf hin, dass die Erfolgschance mit jeder Zunahme von x um eine Einheit um 111 % ansteigt.
Notation
| Begriff | Beschreibung |
|---|---|
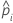 | geschätzte Wahrscheinlichkeit eines Erfolgs für die i-te Zeile in den Daten |
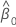 | geschätzter Koeffizient des Schnittpunkts mit der y-Achse |
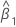 | geschätzter Koeffizient für Prädiktor x |
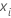 | Datenpunkt für die i-te Zeile |
Varianz-Kovarianz-Matrix
Hierbei handelt es sich um eine d x d-Matrix, wobei d die Anzahl der Prädiktoren plus eins ist. Die Varianz jedes Koeffizienten befindet sich in der Diagonalzelle, und die Kovarianz jedes Koeffizientenpaars befindet sich in der entsprechenden nicht diagonalen Zelle. Die Varianz ist der quadrierte Standardfehler des Koeffizienten.
Die Varianz-Kovarianz-Matrix stammt aus der letzten Iteration der Umkehrung der Informationsmatrix. Die Varianz-Kovarianz-Matrix hat die folgende Form:
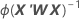
W ist eine Diagonalmatrix, bei der die Diagonalelemente mit der folgenden Formel angegeben werden:

Dabei gilt Folgendes:

Diese Varianz-Kovarianz-Matrix beruht nicht auf der Fisher-Informationsmatrix, sondern auf der beobachteten Hesse-Matrix. Minitab verwendet die beobachtete Hesse-Matrix, da das resultierende Modell robuster gegenüber fehlerhaften Angaben der bedingten Mittelwerte ist.
Wenn die kanonische Linkfunktion verwendet wird, sind die beobachtete Hesse-Matrix und die Fisher-Informationsmatrix identisch.
Notation
| Begriff | Beschreibung |
|---|---|
| yi | Wert der Antwortvariablen für die i-te Zeile |
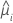 | geschätzter Mittelwert der Antwortvariablen für die i-te Zeile |
| V(·) | Varianzfunktion aus der folgenden Tabelle |
| g(·) | Linkfunktion |
| V '(·) | erste Ableitung der Varianzfunktion |
| g'(·) | erste Ableitung der Linkfunktion |
| g''(·) | zweite Ableitung der Linkfunktion |
Die Varianzfunktion hängt vom Modell ab:
| Modell | Varianzfunktion |
| Binomial | 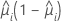 |
| Poisson | 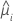 |
Weitere Informationen finden Sie in [1] und [2].
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh und J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
