In diesem Thema
- Schritt 1: Bestimmen, ob die Assoziation zwischen der Antwortvariablen und der Prädiktorvariablen statistisch signifikant ist
- Schritt 2: Verstehen der Effekte der Prädiktoren
- Schritt 3: Bestimmen, wie gut das Modell an die Daten angepasst ist
- Schritt 4: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt
Schritt 1: Bestimmen, ob die Assoziation zwischen der Antwortvariablen und der Prädiktorvariablen statistisch signifikant ist
- p-Wert ≤ α: Die Assoziation ist statistisch signifikant
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und der Prädiktorvariablen besteht.
- p-Wert > α: Die Assoziation ist statistisch nicht signifikant
- Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und der Prädiktorvariablen besteht.
Varianzanalyse
| Quelle | DF | Kor Abw | Kor MW | Chi-Quadrat | p-Wert |
|---|---|---|---|---|---|
| Regression | 1 | 22,7052 | 22,7052 | 22,71 | 0,000 |
| Dosis (mg) | 1 | 22,7052 | 22,7052 | 22,71 | 0,000 |
| Fehler | 4 | 0,9373 | 0,2343 | ||
| Gesamt | 5 | 23,6425 |
Wichtigstes Ergebnis: p-Wert
In diesen Ergebnissen beträgt der p-Wert für die Dosierung 0,000 und liegt somit unter dem Signifikanzniveau 0,05. Diese Ergebnisse weisen darauf hin, dass die Assoziation zwischen der Dosierung und dem Vorhandensein von Bakterien am Ende der Behandlung statistisch relevant ist.
Schritt 2: Verstehen der Effekte der Prädiktoren
Verwenden Sie das Chancenverhältnis, um ein Verständnis des Effekts eines Prädiktors zu erlangen. Minitab berechnet Chancenverhältnisse, wenn das Modell die Logit-Linkfunktion verwendet.
Chancenverhältnisse größer als 1 weisen darauf hin, dass das Ereignis mit umso größerer Wahrscheinlichkeit eintritt, je größer der Prädiktor ist. Chancenverhältnisse kleiner als 1 weisen darauf hin, dass das Ereignis mit umso geringerer Wahrscheinlichkeit eintritt, je größer der Prädiktor ist.
Chancenverhältnisse für stetige Prädiktoren
| Änderungseinheit | Chancenverhältnis | 95%-KI | |
|---|---|---|---|
| Dosis (mg) | 0,5 | 6,1279 | (1,7218; 21,8087) |
Wichtigstes Ergebnis: Chancenverhältnis
In diesen Ergebnissen wird mit dem Modell anhand der Dosierung eines Medikaments das Vorhandensein bzw. Nichtvorhandensein von Bakterien bei erwachsenen Patienten prognostiziert. Jede Tablette enthält eine Dosierung von 0,5 mg, so dass die Forscher die Einheit für eine Änderung auf 0,5 mg festlegen. Das Chancenverhältnis beläuft sich auf etwa 6. Bei jeder weiteren Tablette, die einem Patienten verabreicht wird, steigt die Chance, dass die Bakterien beim Patienten nicht festzustellen sind, um das etwa Sechsfache.
Verwenden Sie die Darstellung der Anpassungslinie, um die Beziehung zwischen der Antwortvariablen und der Prädiktorvariablen zu untersuchen.
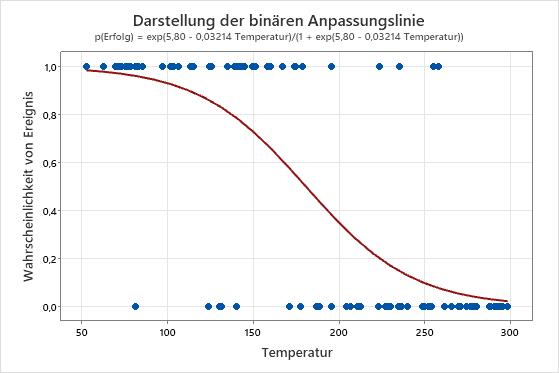
Wichtigstes Ergebnis: Darstellung der binären Anpassungslinie
In diesen Ergebnissen ist die Gleichung als Wahrscheinlichkeit eines Erfolgs formuliert. Der Wert der Antwortvariablen 1 auf der y-Achse stellt einen Erfolg dar. Im Diagramm wird ersichtlich, dass die Erfolgswahrscheinlichkeit mit Zunahme der Temperatur abnimmt. Wenn die Temperaturen in den Daten annähernd 50 betragen, ist die Steigung der Linie nicht sehr steil, was darauf verweist, dass die Wahrscheinlichkeit mit der Zunahme der Temperatur langsam abnimmt. Die Linie ist steiler im mittleren Bereich der Temperaturdaten, was zeigt, dass eine Änderung der Temperatur um 1 Grad in diesem Bereich eine größere Auswirkung hat. Wenn sich die Wahrscheinlichkeit eines Erfolgs am oberen Ende des Temperaturbereichs null annähert, flacht die Linie wieder ab.
Schritt 3: Bestimmen, wie gut das Modell an die Daten angepasst ist
Um zu ermitteln, wie gut das Modell an die Daten angepasst ist, untersuchen Sie die Statistiken in der Tabelle „Zusammenfassung des Modells“. Bei der binären logistischen Regression beeinflusst das Datenformat das R2 der Abweichung, aber nicht das AIC. Weitere Informationen finden Sie unter Wie wirken sich Datenformate bei der binären logistischen Regression auf die Güte der Anpassung aus?.
- R-Qd der Abweichung
-
Je höher das R2 der Abweichung ausfällt, desto besser ist das Modell an die Daten angepasst. Das R2 der Abweichung liegt immer zwischen 0 % und 100 %.
Das R2 der Abweichung nimmt beim Einbinden zusätzlicher Prädiktoren in ein Modell stets zu. Das beste Modell mit fünf Prädiktoren weist beispielsweise immer ein R2 auf, das mindestens so hoch wie das des besten Modells mit vier Prädiktoren ist. Daher ist das R2 der Abweichung am nützlichsten, wenn Sie Modelle derselben Größe vergleichen.
Für die binäre logistische Regression beeinflusst das Format der Daten den Wert des R2 der Abweichung. Im Allgemeinen ist das R2 der Abweichung für Daten im Ereignis-/Versuchsformat höher. Werte des R2 der Abweichung sind nur zwischen Modellen vergleichbar, in denen dasselbe Datenformat verwendet wird.
R2 der Abweichung ist lediglich ein Maß dafür, wie gut das Modell an die Daten angepasst ist. Selbst wenn das Modell ein hohes R2 aufweist, sollten Sie die Residuendiagramme untersuchen, um zu beurteilen, wie gut das Modell an die Daten angepasst ist.
- R-Qd(kor) der Abweichung
-
Verwenden Sie das korrigierte R2 der Abweichung, wenn Sie Modelle vergleichen möchten, die eine unterschiedliche Anzahl von Prädiktoren enthalten. Das R2 der Abweichung nimmt beim Einbinden eines Prädiktors in ein Modell stets zu. Der Wert des korrigierten R2 der Abweichung berücksichtigt die Anzahl der Prädiktoren im Modell, was die Auswahl des richtigen Modells erleichtert.
- AIC, AICc und BIC
- Für Darstellung der binären Anpassungslinie können Sie die Informationskriterien verwenden, um die Anpassung verschiedener Linkfunktionen oder verschiedener Prädiktoren zu vergleichen. Erwünscht sind kleinere Werte. Das Modell mit dem kleinsten Wert ist jedoch nicht zwangsläufig gut an die Daten angepasst. Verwenden Sie auch den Test und die Residuendiagramme, um zu beurteilen, wie gut das Modell an die Daten angepasst ist.
Zusammenfassung des Modells
| R-Qd der Abweichung | R-Qd(kor) der Abweichung | AIC | AICc | BIC | Fläche unter der ROC-Kurve |
|---|---|---|---|---|---|
| 96,04% | 91,81% | 10,63 | 14,63 | 10,22 | 0,9398 |
Wichtigste Ergebnisse: R-Qd der Abweichung, R-Qd(kor) der Abweichung, AIC
In diesen Ergebnissen erklärt das Modell 96,04 % der Abweichung in der Antwortvariablen. Für diese Daten gibt das R2 der Abweichung an, dass das Modell gut an die Daten angepasst ist. Wenn Sie weitere Modelle mit anderen Prädiktoren anpassen, verwenden Sie die anderen Werte, um die Güte der Anpassung der Modelle an die Daten zu vergleichen.
Schritt 4: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt
Verwenden Sie die Residuendiagramme, um zu ermitteln, ob das Modell angemessen ist und die Annahmen der Analyse erfüllt. Wenn die Annahmen nicht erfüllt werden, ist das Modell u. U. nicht gut an die Daten angepasst, und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein.
Weitere Informationen zum Umgang mit Mustern in den Residuendiagrammen finden Sie unter Grafiken für Darstellung der binären Anpassungslinie; klicken Sie dort auf den Namen des Residuendiagramms in der Liste am oberen Rand der Seite.
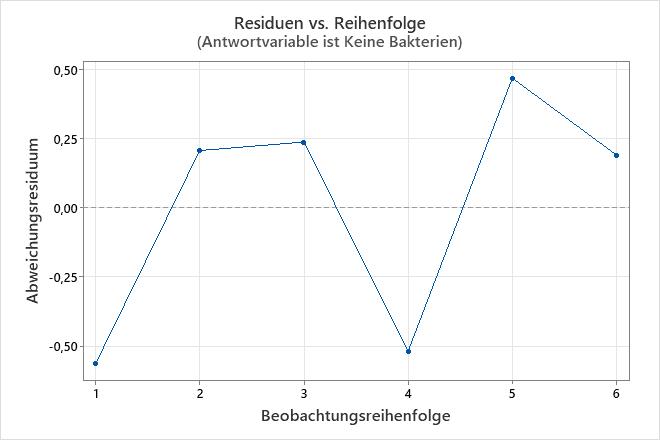
Diagramm der Residuen im Vergleich zu den Anpassungen
Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
Das Diagramm der Residuen im Vergleich zu den Anpassungen ist nur verfügbar, wenn die Daten im Ereignis-/Versuchsformat vorliegen.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Eine ungeeignete Linkfunktion |
| Krümmung | Ein fehlender Term höherer Ordnung oder eine ungeeignete Linkfunktion |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
| Ein in x-Richtung weit von den anderen Punkten entfernter Punkt | Ein einflussreicher Punkt |
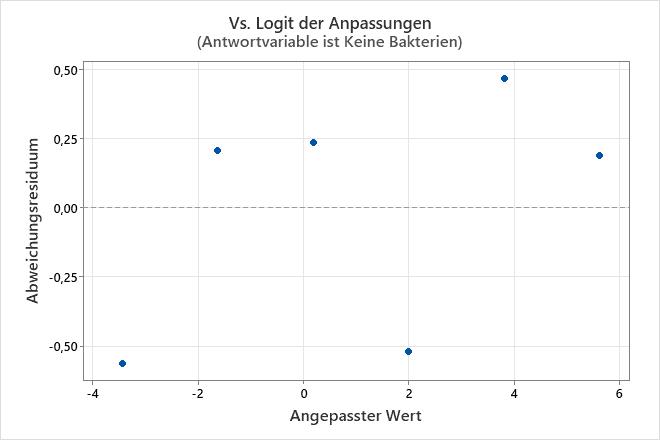
Diagramm der Residuen im Vergleich zur Reihenfolge
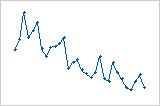
Trend
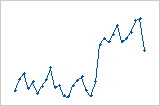
Shift
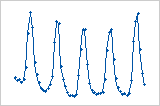
Zyklus