In diesem Thema
Darstellung der binären Anpassungslinie
In der Darstellung der Anpassungslinie werden die Daten der Antwortvariablen und der Prädiktorvariablen angezeigt. Die Darstellung enthält die Regressionslinie, die die Regressionsgleichung abbildet. Sie können auch festlegen, dass das Konfidenzintervall für die angepassten Werte angezeigt werden soll.
Interpretation
Verwenden Sie die Darstellung der Anpassungslinie, um die Beziehung zwischen der Antwortvariablen und der Prädiktorvariablen zu untersuchen.
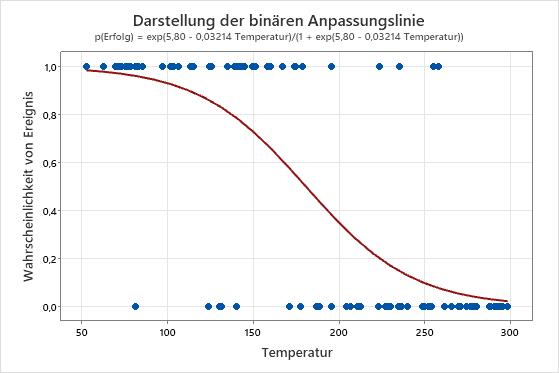
In diesen Ergebnissen ist die Gleichung als Wahrscheinlichkeit eines Erfolgs formuliert. Der Wert der Antwortvariablen 1 auf der y-Achse stellt einen Erfolg dar. Im Diagramm wird ersichtlich, dass die Erfolgswahrscheinlichkeit mit Zunahme der Temperatur abnimmt. Wenn die Temperaturen in den Daten annähernd 50 betragen, ist die Steigung der Linie nicht sehr steil, was darauf verweist, dass die Wahrscheinlichkeit mit der Zunahme der Temperatur langsam abnimmt. Die Linie ist steiler im mittleren Bereich der Temperaturdaten, was zeigt, dass eine Änderung der Temperatur um 1 Grad in diesem Bereich eine größere Auswirkung hat. Wenn sich die Wahrscheinlichkeit eines Erfolgs am oberen Ende des Temperaturbereichs null annähert, flacht die Linie wieder ab.
Wenn das Modell gut an die Daten angepasst ist, zeigen die prognostizierten hohen Wahrscheinlichkeiten an, in welchem Bereich das Ereignis häufig eintritt. Wenn die Temperaturen in den Daten annähernd 50 betragen, tritt am häufigsten der Wert der Antwortvariablen 1 auf. Mit zunehmender Temperatur tritt der Wert der Antwortvariablen 0 häufiger auf.
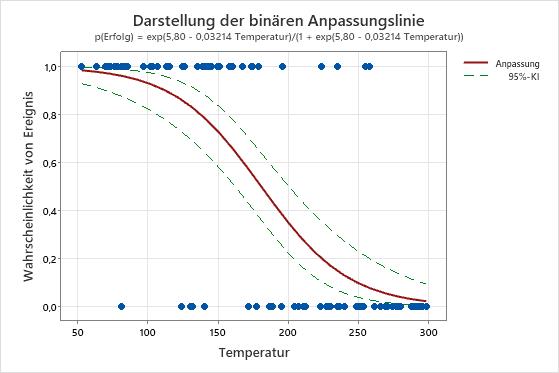
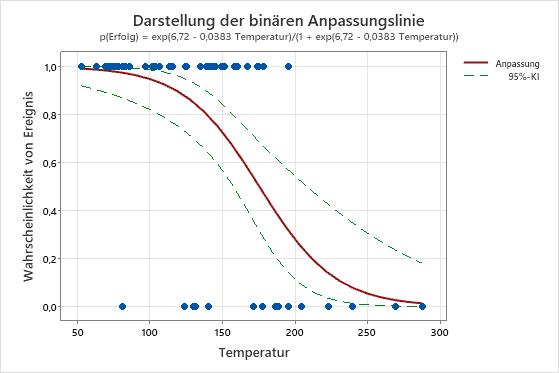
Wenn Sie dem Diagramm Konfidenzintervalle hinzufügen, können Sie anhand der Intervalle beurteilen, wie genau die Schätzwerte der angepassten Werte sind. Im ersten Diagramm unten bleibt der Abstand der Linien für das Konfidenzintervall bei ansteigendem Prädiktor annähernd gleich. Im zweiten Diagramm wird das Konfidenzintervall breiter, wenn der Wert des Prädiktors ansteigt. Das breite Intervall ist teilweise auf die geringe Datenmenge bei hoher Temperatur zurückzuführen.
Histogramm der Residuen
Im Histogramm der Abweichungsresiduen wird die Verteilung der Residuen für alle Beobachtungen veranschaulicht.
Interpretation
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Ein langer Randbereich in einer Richtung | Schiefe |
| Ein Balken weit entfernt von den anderen Balken | Ein Ausreißer |
Da die Darstellung eines Histogramms von der Anzahl der Intervalle abhängt, mit denen die Daten gruppiert werden, verwenden Sie ein Histogramm nicht, um die Normalverteilung der Residuen zu beurteilen. Verwenden Sie dazu stattdessen ein Wahrscheinlichkeitsnetz für Normalverteilung.
Wahrscheinlichkeitsnetz (Normal) für Residuen
Das Wahrscheinlichkeitsnetz (Normal) für Residuen stellt die Residuen im Vergleich zu den Werten dar, die bei Vorliegen einer Normalverteilung erwartet würden.
Interpretation
Verwenden Sie das Wahrscheinlichkeitsnetz (Normal) der Residuen, um die Annahme zu überprüfen, dass die Residuen normalverteilt sind. Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung sollten ungefähr einer Geraden folgen.
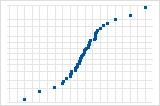
Die S-Kurve deutet auf eine Verteilung mit langen Randbereichen hin.
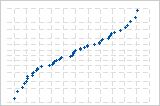
Die invertierte S-Kurve deutet auf eine Verteilung mit kurzen Randbereichen hin.
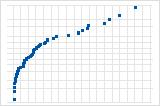
Eine Abwärtskurve deutet auf eine rechtsschiefe Verteilung hin.
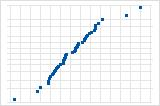
Wenige Punkte, die abseits der Linie liegen, deuten auf eine Verteilung mit Ausreißern hin.
Wenn Sie ein nicht normalverteiltes Muster feststellen, prüfen Sie das Modell anhand der übrigen Residuendiagramme auf andere Probleme, z. B. auf fehlende Terme oder einen Effekt der chronologischen Reihenfolge. Wenn die Residuen keiner Normalverteilung folgen, sind die Konfidenzintervalle der Normal-Approximation und die p-Werte des Wald-Tests möglicherweise ungenau.
Residuen vs. Anpassungen
Im Diagramm der Residuen im Vergleich zu den Anpassungen werden die Residuen auf der y-Achse und die angepassten Werte auf der x-Achse abgetragen. Das Diagramm ist aussagekräftig, wenn die Daten im Ereignis-/Versuchsformat vorliegen. Wenn die Daten im binären Antwort-/Häufigkeitenformat vorliegen, stellt Minitab dieses Diagramm nicht bereit.
Interpretation
Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Eine ungeeignete Linkfunktion |
| Krümmung | Ein fehlender Term höherer Ordnung oder eine ungeeignete Linkfunktion |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
| Ein in x-Richtung weit von den anderen Punkten entfernter Punkt | Ein einflussreicher Punkt |

Diagramm mit Ausreißer
Einer der Punkte ist viel größer als alle anderen Punkte. Daher handelt es sich bei dem Punkt um einen Ausreißer. Wenn zu viele Ausreißer auftreten, ist das Modell möglicherweise nicht akzeptabel. Versuchen Sie nach Möglichkeit, die Ursache von Ausreißern zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
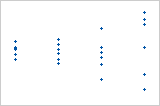
Diagramm mit nicht konstanter Varianz
Die Varianz der Residuen nimmt mit den angepassten Werten zu. Beachten Sie, dass sich bei zunehmenden Werten der Anpassungen die Streuung der Residuen verbreitert. Dieses Muster weist darauf hin, dass die Varianzen der Residuen ungleich (nicht konstant) sind.
| Problem | Mögliche Lösung |
|---|---|
| Nicht konstante Varianz | Erwägen Sie, andere Terme im Modell, eine andere Linkfunktion oder Gewichtungen zu verwenden. |
| Ein Ausreißer oder ein einflussreicher Punkt |
|
Residuen vs. Reihenfolge
Das Diagramm der Residuen im Vergleich zur Reihenfolge zeigt die Residuen in der Reihenfolge an, in der die Daten erfasst wurden.
Interpretation
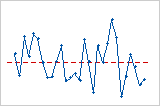
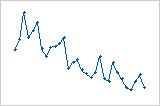
Trend
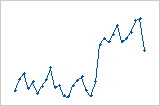
Shift
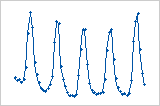
Zyklus
Residuen vs. Variablen
Das Diagramm der Residuen vs. Variablen zeigt die Residuen im Vergleich mit einer anderen Variablen. Die Variable kann bereits im Modell enthalten sein. Es ist auch möglich, dass die Variable nicht im Modell enthalten ist, und Sie vermuten, dass sie die Antwortvariable beeinflusst.
Interpretation
Wenn Sie ein nicht zufälliges Muster in den Residuen feststellen, weist dies darauf hin, dass sich die Variable systematisch auf die Antwortvariable auswirkt. Erwägen Sie, diese Variable in eine Analyse einzubinden.
