Hinweis
Dieser Befehl ist mit dem Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
TreeNet®-Modelle stellen einen Ansatz zum Beheben von Klassifizierungs- und Regressionsproblemen dar, die sowohl genauer als ein einzelner Klassifizierungs- oder Regressionsbaum als auch resistent gegen übermäßige Anpassung sind. Die grobe, allgemeine Beschreibung des Prozesses ist, dass ein kleiner Regressionsbaum das Ausgangsmodell darstellt. Aus diesem Baum ergeben sich Residuen für jede Zeile in den Daten, die zur Antwortvariablen für den nächsten Regressionsbaum werden. Anschließend wird ein weiterer kleiner Regressionsbaum erstellt, um die Residuen aus dem ersten Baum zu prognostizieren und die resultierenden Residuen zu berechnen. Diese Sequenz wiederholen wir, bis eine optimale Anzahl von Bäumen mit minimalem Prädiktionsfehler mithilfe einer Validierungsmethode identifiziert ist. Die resultierende Reihenfolge der Bäume ergibt das TreeNet® Regressionsmodell.
Für den Regressionsfall können wir eine allgemeine Beschreibung der Analyse hinzufügen, aber einige Details hängen davon ab, welche der folgenden Funktionen die Verlustfunktion ist:
| Statistik | Wert |
|---|---|
Anfängliche Anpassung,  |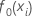
Mittelwert der Antwortvariablen |
Generalisiertes Residuum, 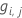 als Wert der Antwortvariablen für Zeile i |
 |
Innerhalb von Knotenaktualisierungen,  |
Mittelwert von  |
| Statistik | Wert |
|---|---|
Anfängliche Anpassung,  |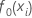
Median der Antwortvariablen |
Generalisiertes Residuum, 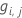 als Wert der Antwortvariablen für Zeile i |
 |
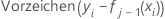Innerhalb von Knotenaktualisierungen,  |
Median von  |
Huber-Verlustfunktion
Für die Huber-Verlustfunktion ist die Statistik wie folgt:
Die anfängliche Anpassung,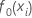 
, entspricht dem Median aller Antwortwerte.
Für den Ausbau des j-ten Baums,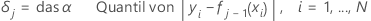 
Dann ist das generalisierte Residuum für die i-te Zeile wie folgt:
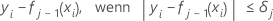
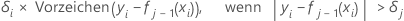
Die generalisierten Residuen werden als Antwortwerte verwendet, um den j-ten Baum aufzubauen.
Der aktualisierte Wert für Zeilen im m-ten Endknoten des j-ten Baums lautet wie folgt:
ist das reguläre Residuum für die i-te Zeile nachdem j-1 Bäume aufgebaut sind. Sei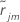 
ist der Median von 
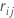sind Werte für Zeilen innerhalb des Endknotens m des j-ten Baums. Dann lautet der aktualisierte Wert für jede Zeile innerhalb des m-ten Endknotens des j-ten Baums:
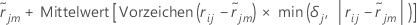
Der Mittelwert im vorherigen Ausdruck wird über alle Zeilen innerhalb des Endknotens m des j-ten Baums berechnet.
Notation für Verlustfunktionen
In den vorstehenden Details,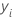 
ist der Wert der Antwortvariablen für Zeile i, 
ist der angepasste Wert aus den vorherigen j – 1 Bäumen und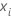 
ist ein Vektor, der die i.-te Zeile der Prädiktorwerte in den Trainingsdaten darstellt.
Eingabeparameter
| Eingabe | Symbol |
|---|---|
| Trainingsrate |  |
| Stichprobenrate |  |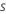
| maximale Anzahl der Endknoten pro Baum |  |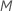
| Anzahl der Bäume |  |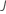
| Umschaltwert |  |
Allgemeiner Prozess
- Zeichnen Sie aus den Trainingsdaten eine Zufallsstichprobe der Größe s * N, wobei N die Anzahl der Zeilen in den Trainingsdaten ist.
- Berechnen Sie die verallgemeinerten Residuen,
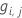, für 
. - Passen Sie einen Regressionsbaum mit höchstens M-Endknoten an die generalisierten Residuen an. Der Baum unterteilt die Beobachtungen in höchstens M sich gegenseitig ausschließende Gruppen.
- Berechnen Sie für den m-ten Endknoten im Regressionsbaum die Aktualisierungen innerhalb der Knoten des Baums, die von der Verlustfunktion abhängen,
. - Reduzieren Sie die Aktualisierungen innerhalb der Knoten um die Trainingsrate, und wenden Sie die Werte an, um die aktualisierten angepassten Werte zu erhalten,
:
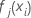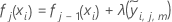
- Wiederholen Sie die Schritte 1–5 für jeden der J-Bäume in der Analyse.
