Hinweis
Dieser Befehl ist mit Predictive Analytics-Modul. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
Ein Forscherteam will anhand von Daten aus einem Spritzgießprozess Einstellungen für Maschinen untersuchen, die eine bestimmte Art von Festigkeit eines Kunststoffteils maximieren. Zu den Variablen gehören Steuerungen an den Maschinen, verschiedene Kunststoffformeln und die Spritzgießmaschinen.
Im Rahmen der ersten Erkundung der Daten entscheiden sich die Forscher für Ermitteln von wichtigen Prädiktoren den Vergleich von Modellen, indem sie nacheinander unwichtige Prädiktoren entfernen, um wichtige Prädiktoren zu identifizieren. Die Forscher hoffen, wichtige Prädiktoren zu identifizieren, die den größten Einfluss haben und mehr Einblick in die Beziehungen zwischen der Antwort und den wichtigsten Prädiktoren zu gewinnen.
- Öffnen Sie den Beispieldatensatz Injektionsprozess.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antwort den Wert Stärke ein.
- Geben Sie Injektionsdruck-'Temperatur bei der Messung' in Stetige Prädiktoren.
- Geben Sie im Feld Kategoriale Prädiktoren die Spalten Maschine und Formel ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
Für diese Analyse vergleicht Minitab Statistical Software 20 Modelle. Das Sternchen in der Spalte „Modell“ der Tabelle Modellauswertung zeigt, dass das Modell mit dem größten Wert der kreuzvalidierten R2-Statistik Modell 16 ist. Modell 16 enthält 5 wichtige Prädiktoren. Die Ergebnisse, die der Modellauswertungstabelle folgen, beziehen sich auf Modell 16.
Obwohl Modell 16 den größten Wert der kreuzvalidierten R2-Statistik hat, weisen andere Modelle ähnliche Werte auf. Das Team kann auf Alternatives Modell auswählen klicken, um Ergebnisse für andere Modelle aus der Tabelle Modellauswertung zu erstellen.
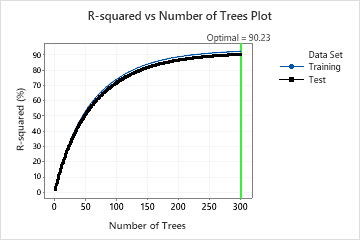
In den Ergebnissen für Modell 16 zeigt das Diagramm von R-Quadrat vs. Anzahl der Bäume, dass die optimale Anzahl von Bäumen der Anzahl der Bäume in der Analyse entspricht, 300. Das Team kann auf Optimieren von Hyperparametern klicken, um die Anzahl der Bäume zu erhöhen und zu sehen, ob Änderungen an anderen Hyperparametern die Leistung des Modells verbessern.
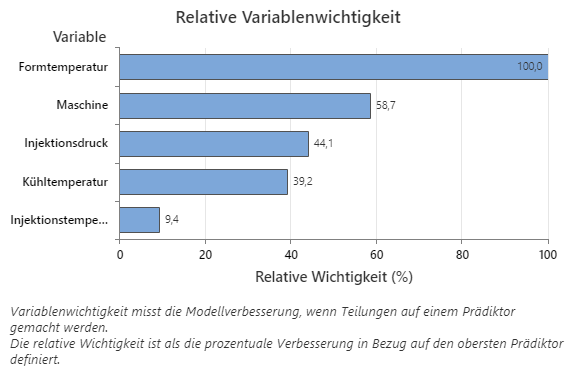
Das Diagramm „Relative Variablenwichtigkeit“ zeigt die Prädiktoren in der Reihenfolge ihrer Auswirkungen auf die Modellverbesserung, wenn Teilungen anhand eines Prädiktors über die Abfolge der Bäume hinweg vorgenommen werden. Die wichtigste Prädiktorvariable ist die Formtemperatur. Wenn die Wichtigkeit der obersten Prädiktorvariablen, „Formtemperatur“, 100 % beträgt, hat die nächstwichtige Variable, „Maschine“, einen Beitrag von 58,7 %. Das bedeutet, dass die Maschine, die einspritzt, zu 58,7 % so wichtig ist wie die Temperatur im Inneren der Form.
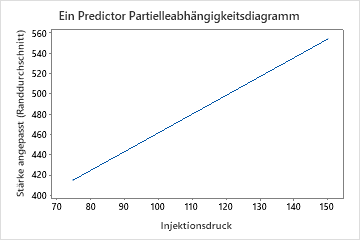
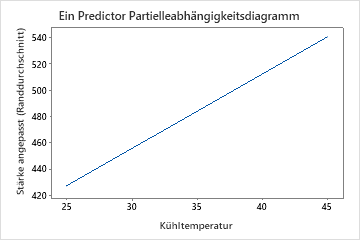
Verwenden Sie die Diagramme der partiellen Abhängigkeit, um zu erfahren, wie sich die wichtigen Variablen oder Variablenpaare auf den prognostizierten Wert der Antwortvariablen auswirken. Die Diagramme der partiellen Abhängigkeit zeigen, ob die Beziehung zwischen der Antwortvariablen und einer Variablen linear, monoton oder komplexer ist.
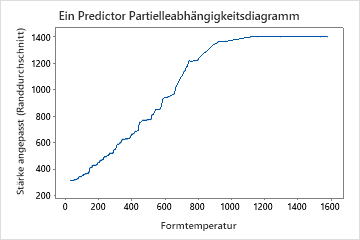
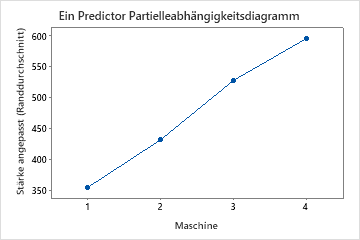
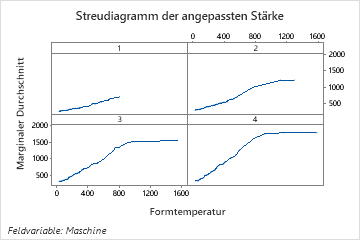
Die Diagramme der partiellen Abhängigkeit bei einem Prädiktor zeigen, dass Formtemperatur, Einspritzdruck und Kühltemperatur alle einen positiven Bezug zur Festigkeit haben. Das Diagramm der Maschinen zeigt die Unterschiede zwischen den Maschinen, wobei Maschine 1 im Durchschnitt die schwächsten Teile und Maschine 4 im Durchschnitt die stärksten Teile herstellt. Das Team stellt fest, dass die Formtemperatur und die Maschine die stärkste Wechselwirkung in den Daten haben, also betrachten Sie das Diagramm der partiellen Abhängigkeit, um besser zu verstehen, wie diese Variablen die Festigkeit beeinflussen. Das Team kann in den Ergebnissen auswählen , um Diagramme für andere Variablen zu erstellen, z. B. die Einspritztemperatur.
Das Diagramm der partiellen Abhängigkeit bei zwei Prädiktoren „Formtemperatur und Maschine“ gibt einen Einblick in die unterschiedlichen durchschnittlichen Festigkeiten der Maschinen. Ein Grund ist, dass die Daten von Maschine 1 nicht so viele Beobachtungen bei den höchsten Formtemperaturen enthalten wie die anderen Maschinen. Das Team könnte sich immer noch entscheiden, nach anderen Gründen zu suchen, dass die Maschinen unterschiedliche Festigkeiten erzeugen, wenn andere Einstellungen identisch sind. Das Team kann auf die Ergebnisse klicken , um Diagramme für andere Variablenpaare zu erstellen.
Methode
| Verlustfunktion | Quadrierter Fehler |
|---|---|
| Kriterium für Auswahl der optimalen Anzahl von Bäumen | Maximales R-Quadrat |
| Modellvalidierung | Kreuzvalidierung mit 3 Faltungen |
| Trainingsrate | 0,01408 |
| Teilstichprobenfraktion | 0,5 |
| Maximale Anzahl von Endknoten pro Baum | 6 |
| Minimale Endknotengröße | 3 |
| Anzahl der für die Knotenteilung ausgewählten Prädiktoren | Gesamtanzahl der Prädiktoren = 21 |
| Verwendete Zeilen | 1408 |
Informationen zur Antwortvariablen
| Mittelwert | StdAbw | Minimum | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 485,247 | 318,611 | 41,2082 | 301,099 | 398,924 | 562,449 | 2569,04 |
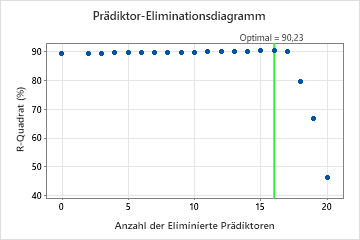
Modellauswahl durch Eliminierung unwichtiger Prädiktoren
| Modell | Optimale Anzahl von Bäumen | R-Quadrat (%) | Anzahl der Prädiktoren | Eliminierte Prädiktoren |
|---|---|---|---|---|
| 1 | 300 | 89,32 | 21 | Keine |
| 2 | 300 | 89,34 | 19 | Kunststoffdurchfluss; Position ändern |
| 3 | 300 | 89,39 | 18 | Trocknungstemperatur |
| 4 | 300 | 89,46 | 17 | Schmelztemperaturzone 2 |
| 5 | 300 | 89,51 | 16 | Kunststofftemperatur |
| 6 | 300 | 89,50 | 15 | Formel |
| 7 | 300 | 89,59 | 14 | Haltedruck |
| 8 | 300 | 89,57 | 13 | Schraubenkissen |
| 9 | 300 | 89,69 | 12 | Schmelztemperaturzone 4 |
| 10 | 300 | 89,70 | 11 | Rückdruck |
| 11 | 300 | 89,86 | 10 | Schmelztemperaturzone 1 |
| 12 | 300 | 89,90 | 9 | Trocknungszeit |
| 13 | 300 | 89,92 | 8 | Temperatur bei der Messung |
| 14 | 300 | 90,06 | 7 | Schmelztemperaturzone 5 |
| 15 | 300 | 90,16 | 6 | Schmelztemperaturzone 3 |
| 16* | 300 | 90,23 | 5 | Schraubendrehzahl |
| 17 | 300 | 89,96 | 4 | Injektionstemperatur |
| 18 | 297 | 79,37 | 3 | Kühltemperatur |
| 19 | 244 | 66,64 | 2 | Injektionsdruck |
| 20 | 164 | 46,19 | 1 | Maschine |
Zusammenfassung des Modells
| Prädiktoren gesamt | 5 |
|---|---|
| Wichtige Prädiktoren | 5 |
| Anzahl der aufgebauten Bäume | 300 |
| Optimale Anzahl von Bäumen | 300 |
| Statistiken | Trainings | Test |
|---|---|---|
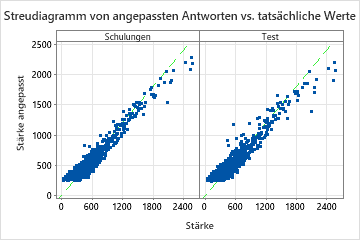
| R-Quadrat | 92,23% | 90,23% |
| Wurzel des mittleren quadrierten Fehlers (RMSE) | 88,8049 | 99,5673 |
| Mittlerer quadrierter Fehler (MSE) | 7886,3152 | 9913,6420 |
| Mittlere abs. Abweichung (MAD) | 68,9231 | 74,4113 |
| Mittlerer absoluter prozentualer Fehler (MAPE) | 0,2083 | 0,2175 |