Hinweis
Dieser Befehl ist mit Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
Ein Forscherteam möchte Daten über einen Kreditnehmer und den Ort einer Immobilie nutzen, um den Hypothekenbetrag zu prognostizieren. Variablen sind Einkommen, Ethnie und Geschlecht des Kreditnehmers sowie der Zählbezirk der Immobilie sowie andere Informationen über den Kreditnehmer und den Objekttyp.
Nach einer ersten Erkundung CART® Regression zur Identifizierung der wichtigen Prädiktoren betrachtet TreeNet® Regression das Team nun einen notwendigen Folgeschritt. Die Forscher hoffen, einen tieferen Einblick in die Beziehungen zwischen der Antwortvariablen und den wichtigsten Prädiktoren zu erhalten und neue Beobachtungen mit größerer Genauigkeit prognostizieren zu können.
Diese Daten sind eine Adaption eines öffentlichen Datensatzes, der Informationen zu Hypotheken von Bundesbausparkassen enthält. Die Originaldaten stammen von fhfa.gov.
- Öffnen Sie den Beispieldatensatz GekaufteHypotheken.MTW.
- Wählen Sie aus.
- Geben Sie im Feld Antwort den Wert Kreditbetrag ein.
- Geben Sie Jahreseinkommen-Einkommen Bezirk in Stetige Prädiktoren.
- Geben Sie Immobilien-Erstkäufer–Statistisches Kerngebiet in Kategoriale Prädiktoren.
- Klicken Sie auf Validierung.
- Wählen Sie im Feld Validierungsmethode die Option Kreuzvalidierung mit K Faltungen aus.
- Geben Sie im Feld Anzahl der Faltungen (K) den Wert 3 ein.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
Für diese Analyse baut Minitab 300 Bäume auf, und die optimale Anzahl von Bäumen beträgt 300. Da die optimale Anzahl von Bäumen nahe an der maximalen Anzahl von Bäumen liegt, die das Modell aufbaut, wiederholen die Forscher die Analyse mit mehr Bäumen.
Zusammenfassung des Modells
| Prädiktoren gesamt | 34 |
|---|---|
| Wichtige Prädiktoren | 19 |
| Anzahl der aufgebauten Bäume | 300 |
| Optimale Anzahl von Bäumen | 300 |
| Statistiken | Trainings | Test |
|---|---|---|
| R-Quadrat | 94,02% | 84,97% |
| Wurzel des mittleren quadrierten Fehlers (RMSE) | 32334,5587 | 51227,9431 |
| Mittlerer quadrierter Fehler (MSE) | 1,04552E+09 | 2,62430E+09 |
| Mittlere abs. Abweichung (MAD) | 22740,1020 | 35974,9695 |
| Mittlerer absoluter prozentualer Fehler (MAPE) | 0,1238 | 0,1969 |
Beispiel mit 500 Bäumen
- Wählen Sie in den Ergebnissen aus Optimieren von Hyperparametern.
- Geben Sie im Feld Anzahl der Bäume den Wert 500 ein.
- Klicken Sie auf Anzeigen der Ergebnisse.
Interpretieren der Ergebnisse
Für diese Analyse wurden 500 Bäume aufgebaut und die optimale Anzahl von Bäumen für die Kombination von Hyperparametern mit dem besten Wert des Genauigkeitskriteriums ist 500. Die Fraktion für die Teilstichprobe ändert sich auf 0,7 anstelle der 0,5 in der ursprünglichen Analyse. Die Trainingsrate ändert sich auf 0,0437 anstelle von 0,04372 in der ursprünglichen Analyse.
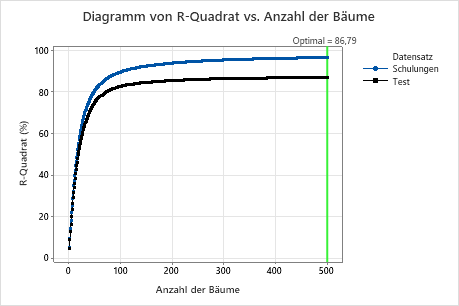
Untersuchen Sie sowohl die Tabelle mit der Zusammenfassung des Modells als auch das Diagramm von R-Quadrat vs. Anzahl der Bäume. Der R2-Wert bei einer Anzahl von 500 Bäumen beträgt 86,79 % für die Testdaten und 96,41 % für die Trainingsdaten. Diese Ergebnisse zeigen eine Verbesserung gegenüber einer herkömmlichen Regressionsanalyse und einer CART® Regression.
Methode
| Verlustfunktion | Quadrierter Fehler |
|---|---|
| Kriterium für Auswahl der optimalen Anzahl von Bäumen | Maximales R-Quadrat |
| Modellvalidierung | Kreuzvalidierung mit 3 Faltungen |
| Trainingsrate | 0,04372 |
| Teilstichprobenfraktion | 0,5 |
| Maximale Anzahl von Endknoten pro Baum | 6 |
| Minimale Endknotengröße | 3 |
| Anzahl der für die Knotenteilung ausgewählten Prädiktoren | Gesamtanzahl der Prädiktoren = 34 |
| Verwendete Zeilen | 4372 |
Informationen zur Antwortvariablen
| Mittelwert | StdAbw | Minimum | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
Methode
| Verlustfunktion | Quadrierter Fehler |
|---|---|
| Kriterium für Auswahl der optimalen Anzahl von Bäumen | Maximales R-Quadrat |
| Modellvalidierung | Kreuzvalidierung mit 3 Faltungen |
| Trainingsrate | 0,001; 0,0437; 0,1 |
| Teilstichprobenfraktion | 0,5; 0,7 |
| Maximale Anzahl von Endknoten pro Baum | 6 |
| Minimale Endknotengröße | 3 |
| Anzahl der für die Knotenteilung ausgewählten Prädiktoren | Gesamtanzahl der Prädiktoren = 34 |
| Verwendete Zeilen | 4372 |
Informationen zur Antwortvariablen
| Mittelwert | StdAbw | Minimum | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
Optimierung der Hyperparameter
| Modell | Optimale Anzahl von Bäumen | R-Quadrat (%) | Mittlere absolute Abweichung | Trainingsrate | Teilstichprobenfraktion | Maximale Anzahl von Endknoten |
|---|---|---|---|---|---|---|
| 1 | 500 | 36,43 | 82617,1 | 0,0010 | 0,5 | 6 |
| 2 | 495 | 85,87 | 34560,5 | 0,0437 | 0,5 | 6 |
| 3 | 495 | 85,63 | 34889,3 | 0,1000 | 0,5 | 6 |
| 4 | 500 | 36,86 | 82145,0 | 0,0010 | 0,7 | 6 |
| 5* | 500 | 86,79 | 33052,6 | 0,0437 | 0,7 | 6 |
| 6 | 451 | 86,67 | 33262,3 | 0,1000 | 0,7 | 6 |
Zusammenfassung des Modells
| Prädiktoren gesamt | 34 |
|---|---|
| Wichtige Prädiktoren | 24 |
| Anzahl der aufgebauten Bäume | 500 |
| Optimale Anzahl von Bäumen | 500 |
| Statistiken | Trainings | Test |
|---|---|---|
| R-Quadrat | 96,41% | 86,79% |
| Wurzel des mittleren quadrierten Fehlers (RMSE) | 25035,7243 | 48029,9503 |
| Mittlerer quadrierter Fehler (MSE) | 6,26787E+08 | 2,30688E+09 |
| Mittlere abs. Abweichung (MAD) | 17309,3936 | 33052,6087 |
| Mittlerer absoluter prozentualer Fehler (MAPE) | 0,0930 | 0,1790 |
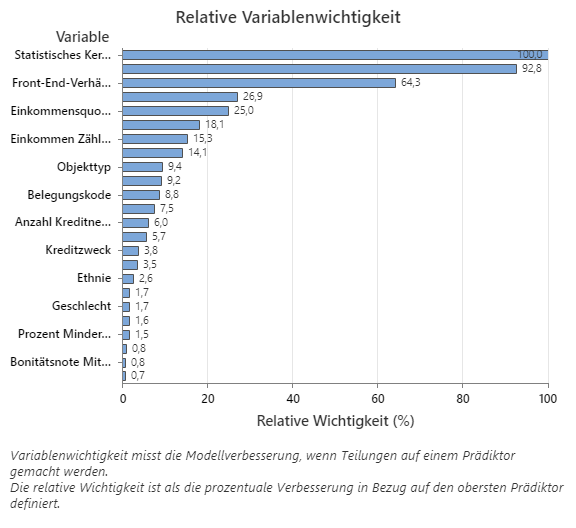
Das Diagramm „Relative Variablenwichtigkeit“ zeigt die Prädiktoren in der Reihenfolge ihrer Auswirkungen auf die Modellverbesserung, wenn Teilungen anhand eines Prädiktors über die Abfolge der Bäume hinweg vorgenommen werden. Die wichtigste Prädiktorvariable ist „Statistisches Kerngebiet“. Wenn die Wichtigkeit der obersten Prädiktorvariablen, „Statistisches Kerngebiet“, 100 % beträgt, hat die nächstwichtigste Variable, „Jahreseinkommen“, einen Beitrag von 92,8%. Dies bedeutet, dass das Jahreseinkommen des Kreditnehmers zu 92,8% so wichtig ist wie die geografische Lage der Immobilie.
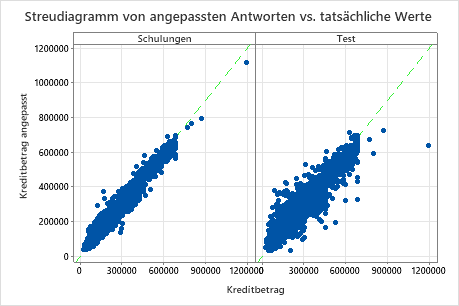
Das Streudiagramm der angepassten Kreditbeträge im Vergleich zu den tatsächlichen Kreditbeträgen zeigt die Beziehung zwischen den angepassten und tatsächlichen Werten sowohl für die Trainingsdaten als auch für die Testdaten. Sie können mit dem Mauszeiger auf die Punkte im Diagramm zeigen, um die dargestellten Werte leichter sehen zu können. In diesem Beispiel fallen alle Punkte ungefähr in die Nähe der Referenzlinie von y=x.
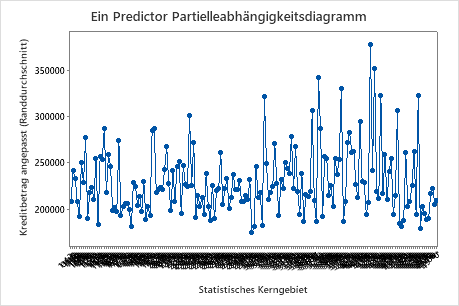
Verwenden Sie die partiellen Abhängigkeitsdiagramme, um einen Einblick in die Auswirkungen der wichtigen Variablen oder Variablenpaare auf die angepassten Antwortwerte zu erhalten. Die Diagramme der partiellen Abhängigkeit zeigen, ob die Beziehung zwischen der Antwortvariablen und einer Variablen linear, monoton oder komplexer ist.
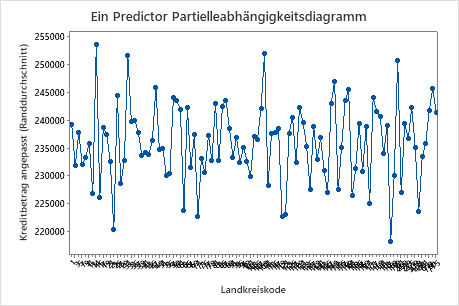
Das erste Diagramm veranschaulicht den angepassten Kreditbetrag für jedes statistische Kerngebiet. Da es so viele Datenpunkte gibt, können Sie mit dem den Cursor auf die einzelnen Datenpunkten zeigen, um die betreffenden x- und y-Werte zu sehen. Der höchste Punkt auf der rechten Seite der Grafik steht für Kerngebiet Nummer 41860, und der angepasste Kreditbetrag liegt bei rund 378069$.
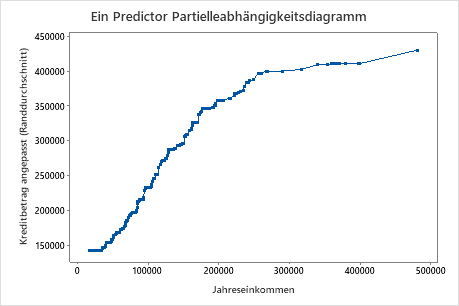
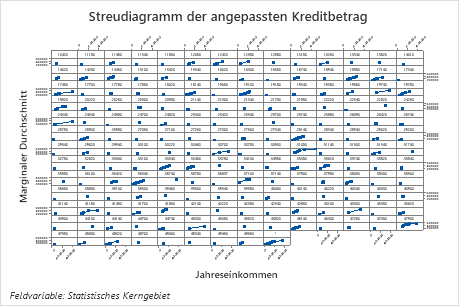
Das zweite Diagramm zeigt, dass der angepasste Kreditbetrag mit der Höhe des Jahreseinkommens steigt. Nachdem das Jahreseinkommen 300.000 $ erreicht hat, steigt der angepasste Kreditbetrag langsamer an.
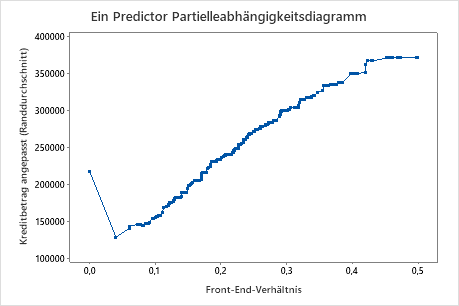
Das dritte Diagramm zeigt, dass der angepasste Kreditbetrag steigt, wenn das Front-End-Verhältnis steigt.
Das vierte Diagramm veranschaulicht den angepassten Kreditbetrag für jeden Landkreiskode der Volkszählung. Wie beim ersten Diagramm können Sie mit dem Cursor auf bestimmte Datenpunkte zeigen, um mehr Informationen zu erhalten. Wählen Sie oder aus, um Diagramme für andere Variablen zu erstellen.
