Hinweis
Dieser Befehl ist mit dem Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
Wichtige Prädiktoren
- Ermitteln Sie die Reduzierung der mittleren quadrierten Fehler, wenn der Prädiktor einen Knoten aufteilt.
- Fügen Sie alle Reduzierungen von allen Knoten hinzu, bei denen der Prädiktor der Knotenteiler ist.
Dann entspricht der Wichtigkeitswert für den Prädiktor der Summe der Modellverbesserungswerte für alle Bäume.

Durchschnittliche –Log-Likelihood für eine binäre Antwortvariable
Trainingsdaten oder keine Validierung
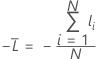
Dabei gilt Folgendes:
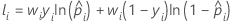
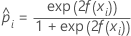
Notation für Trainingsdaten oder keine Validierung
| Begriff | Beschreibung |
|---|---|
| N | Stichprobenumfang des vollständigen Datensatzes oder Trainingsdatensatzes |
| wi | Gewichtung für die i-te Beobachtung im ganzen Datensatz oder im Trainingsdatensatz |
| yi | i-te Antwortvariable, die für den vollständigen oder Trainingsdatensatz 1 für das Ereignis und andernfalls 0 ist |
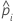 | prognostizierte Wahrscheinlichkeit des Ereignisses für die i-te Zeile im vollständigen oder Trainingsdatensatz |
 | angepasster Wert aus dem Modell |
Kreuzvalidierung mit K Faltungen
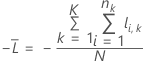
Dabei gilt Folgendes:
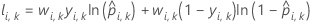

Notation für Kreuzvalidierung mit K Faltungen
| Begriff | Beschreibung |
|---|---|
| N | Stichprobenumfang der vollständigen Daten oder Trainingsdaten |
| nk | Stichprobenumfang der Faltung k |
| wi, k | Gewichtung für die i-te Beobachtung in Faltung j |
| yi, k | binärer Antwortwert von Fall i in Faltung k. yi, k= 1 für Ereignisklasse, sonst 0. |
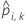 | prognostizierte Wahrscheinlichkeit für Fall i in Faltung k. Die prognostizierte Wahrscheinlichkeit stammt aus dem Modell, das die Daten in Faltung k nicht verwendet. |
 | angepasster Wert für Fall i in Faltung k. Der angepasste Wert stammt aus dem Modell, das die Daten in Faltung k nicht verwendet. |
Testdatensatz

Dabei gilt Folgendes:
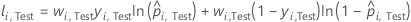
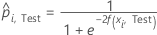
Notation für Testdatensatz
| Begriff | Beschreibung |
|---|---|
| nTest | Stichprobenumfang des Testdatensatzes |
| wi, Test | Gewichtung für die i-te Beobachtung im Testdatensatz |
| yi, Test | binärer Antwortwert von Fall i in Faltung k im Testdatensatz. yi, k = 1 für Ereignisklasse, sonst 0. |
 | prognostizierte Wahrscheinlichkeit für Fall i im Testdatensatz |
 | angepasster Wert für Fall i im Testdatensatz |
Durchschnittliche –Log-Likelihood für eine multinomiale Antwort
 die Anzahl der Stufen in der Antwortvariablen.
die Anzahl der Stufen in der Antwortvariablen. Trainingsdaten oder keine Validierung
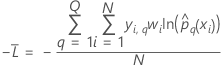
Dabei gilt Folgendes:
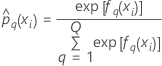
Notation für Trainingsdaten oder keine Validierung
| Begriff | Beschreibung |
|---|---|
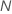 | Stichprobenumfang des vollständigen Datensatzes oder Trainingsdatensatzes |
| wi | Gewichtung für die i-te Beobachtung im ganzen Datensatz oder im Trainingsdatensatz |
| yi, q | i-ter Antwortwert, der 1 ist, wenn 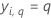 und sonst 0 und sonst 0 |
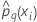 | prognostizierte Wahrscheinlichkeit der q-ten Stufe der Antwortvariablen für die i-te Zeile im vollständigen oder Trainingsdatensatz |
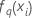 | angepasster Wert aus der q-ten Sequenz der Bäume für die i-te Zeile, die verwendet wird, um die prognostizierte Wahrscheinlichkeit der q-ten Stufe der Antwortvariablen zu berechnen |
Kreuzvalidierung mit K Faltungen
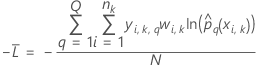
Dabei gilt Folgendes:
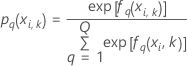
Notation für Kreuzvalidierung mit K Faltungen
| Begriff | Beschreibung |
|---|---|
| N | Stichprobenumfang der Trainingsdaten |
| nk | Stichprobenumfang der Faltung k |
| wi, k | Gewichtung für die i-te Beobachtung in Faltung j |
| yi, k, q | i-ter Antwortwert des Falles i in Faltung k der 1 ist, wenn  und sonst 0. und sonst 0. |
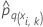 | Die prognostizierte Wahrscheinlichkeit der q-ten Stufe der Antwortvariablen für die i-te Reihe in Faltung k. Die prognostizierte Wahrscheinlichkeit stammt aus dem Modell, das die Daten in Faltung k nicht verwendet. |
 | Der angepasste Wert aus der q-ten Sequenz von Bäumen für die i-te Reihe in Faltung k, die verwendet wird, um die prognostizierte Wahrscheinlichkeit der q-ten Ebene der Antwortvariablen zu berechnen. Der angepasste Wert stammt aus dem Modell, das die Daten in Faltung k nicht verwendet. |
Testdatensatz

Dabei gilt Folgendes:
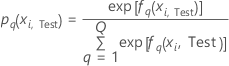
Notation für Testdatensatz
| Begriff | Beschreibung |
|---|---|
| nTest | Stichprobenumfang des Testdatensatzes |
| wi, Test | Gewichtung für die i-te Beobachtung im Testdatensatz |
| yi, Test, q | i-ter Antwortwert von Fall i im Testdatensatz, der 1 ist, wenn 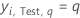 und sonst 0. und sonst 0. |
 | Die prognostizierte Wahrscheinlichkeit der q-ten Stufe der Antwortvariablen für die i-te Zeile in den Testdaten. Die prognostizierte Wahrscheinlichkeit stammt aus dem Modell, das den Testdatensatz nicht verwendet. |
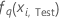 | Der angepasste Wert für die q-te Sequenz von Bäumen für die i-te Zeile im Testdatensatz, die verwendet wird, um die prognostizierte Wahrscheinlichkeit der q-ten Ebene der Antwortvariablen zu berechnen. Die prognostizierte Wahrscheinlichkeit stammt aus dem Modell, das den Testdatensatz nicht verwendet. |
Fläche unterhalb der ROC-Kurve
Formel


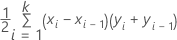
Hierbei ist k die Anzahl der eindeutigen Ereigniswahrscheinlichkeiten und (x0, y0) ist der Punkt (0, 0).
Um die Fläche für eine Kurve anhand eines Testdatensatzes oder von kreuzvalidierten Daten zu berechnen, verwenden Sie die Punkte aus der entsprechenden Kurve.
Notation
| Begriff | Beschreibung |
|---|---|
| TPR | Richtig-Positiv-Rate |
| FPR | Falsch-Positiv-Rate |
| TP | Richtig positiv; Ereignisse, die richtig bewertet wurden |
| FN | falsch negativ, Ereignisse, die falsch bewertet wurden |
| P | Anzahl der tatsächlichen positiven Ereignisse |
| FP | falsch positiv, Nicht-Ereignisse, die falsch bewertet wurden |
| N | Anzahl der tatsächlichen negativen Ereignisse |
| FNR | Falsch-Negativ-Rate |
| TNR | Richtig-Negativ-Rate |
Beispiel
| x (Falsch-Positiv-Rate) | y (Richtig-Positiv-Rate) |
|---|---|
| 0,0923 | 0,3051 |
| 0,4154 | 0,7288 |
| 0,7538 | 0,9322 |
| 1 | 1 |
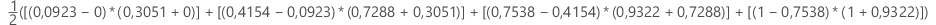

95%-KI für die Fläche unterhalb der ROC-Kurve
Das folgende Intervall gibt die Ober- und die Untergrenze für das Konfidenzintervall an:
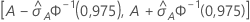
Die Berechnung des Standardfehlers der Fläche unterhalb der ROC-Kurve (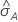 ) stammt aus dem Salford Predictive Modeler®. Allgemeine Informationen zum Schätzen der Varianz der Fläche unterhalb ROC-Kurve finden Sie in den folgenden Veröffentlichungen:
) stammt aus dem Salford Predictive Modeler®. Allgemeine Informationen zum Schätzen der Varianz der Fläche unterhalb ROC-Kurve finden Sie in den folgenden Veröffentlichungen:
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations. In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer. doi:10.1007/978-3-642-16114-8
Cortes, C. and Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305–312.
Feng, D., Cortese, G., und Baumgartner, R. (2017). A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size. Statistical Methods in Medical Research, 26(6), 2603–2621. doi:10.1177/0962280215602040
Notation
| Begriff | Beschreibung |
|---|---|
| A | Fläche unterhalb der ROC-Kurve |
 | 0,975 Perzentil der Standardnormalverteilung |
Lift
Allgemeine Berechnungen für den kumulativen Lift finden Sie unter Methoden und Formeln für das Lift-Diagramm für Anpassen des Modells und Ermitteln von wichtigen Prädiktoren mit TreeNet®-Klassifikation.
Fehlklassifizierungsrate
Verwenden Sie im Fall mit Gewichtungen die Anzahlen gewichtet anstelle von Anzahlen.

Für die Kreuzvalidierung mit K Faltungen ist die fehlklassifizierte Anzahl die Summe der Fehlklassifikationen, wenn die einzelnen Faltungen als Testdatensatz verwendet werden.
Für die Validierung mit einem Testdatensatz ist die fehlklassifizierte Anzahl die Summe der Fehlklassifikationen im Testdatensatz, und die Gesamtanzahl bezieht sich auf den Testdatensatz.
