Hinweis
Dieser Befehl ist mit dem Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
Wichtige Variablen
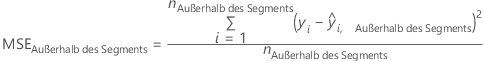
| Begriff | Beschreibung |
|---|---|
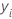 | Wert der Antwortvariablen für Zeile i |
 | Anzahl von Zeilen, die in den Daten von außerhalb des Segments über den gesamten Wald angezeigt werden |
 | Prognose für Daten von außerhalb des Segments für Zeile i |
Permutieren Sie dann die Werte einer Variablen xm nach dem Zufallsprinzip durch die Daten von außerhalb des Segments. Lassen Sie die Antwortwerte und die anderen Prädiktorwerte gleich. Verwenden Sie dann die gleichen Schritte zur Berechnung des mittleren quadrierter Fehlers für die permutierten Daten,  .
.
Die Wichtigkeit für die Variable xm ergibt sich aus der Differenz der beiden mittleren quadrierten Fehler:

Minitab rundet Werte kleiner als 10–7 auf 0.

Prognosen für Daten von außerhalb des Segments und Testdaten
Die prognostizierten Berechnungen für die folgenden Maße der Modellgenauigkeit hängen von der Validierungsmethode ab. Die Prognose für Daten von außerhalb des Segments kommen nur von den Bäumen, bei denen eine Zeile Daten von außerhalb des Segments umfasst. Klassifizieren Sie für einen bestimmten Baum j in der Analyse die Daten von außerhalb des Segments mit dem Baum. Wiederholen Sie diese Prognose für jeden Baum im Wald. Berechnen Sie dann den Durchschnitt der Prognosen von außerhalb des Segments für jede Zeile, die mindestens einmal in den Daten von außerhalb des Segments vorkommt. Bei der Auswertung des Modells mit den Daten von außerhalb des Segments ist der Durchschnitt der Antwortvariablen der Durchschnitt aller Zeilen in den Daten von außerhalb des Segments.
Verwenden Sie für den Testdatensatz jeden Baum im Wald, um jeden Wert im Testdatensatz zu prognostizieren. Bilden Sie dann den Durchschnitt der Prognosen von allen Bäumen, um die Prognose für das Modell zu erhalten. Bei der Auswertung des Modells mit dem Testdatensatz ist die durchschnittliche Antwort der Durchschnitt der Zeilen im Testdatensatz.
R-Quadrat
Bei der Berechnung von R2 werden die Daten von außerhalb des Segments oder der Testdatensatz verwendet. Die Prognosen unterscheiden sich in diesen beiden Fällen. Im Allgemeinen hat die Formel für R2 folgendes Format:

Wurzel des mittleren quadrierten Fehlers (RMSE)

Mittlerer quadrierter Fehler (MSE)
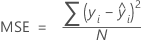
Mittlere absolute Abweichung (MAD)
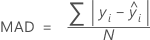
Mittlerer absoluter prozentualer Fehler (MAPE)

Notation
| Begriff | Beschreibung |
|---|---|
| yi | 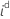 beobachteter Wert der Antwortvariablen beobachteter Wert der Antwortvariablen |
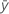 | Mittelwert der Antwortvariablen |
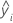 | prognostizierter Wert der Antwortvariablen für Zeile 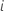 |
| N | Anzahl der Zeilen |
