Hinweis
Dieser Befehl ist mit Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
Ein Forscherteam sammelt Daten aus dem Verkauf einzelner Wohnimmobilien in Ames im US-Bundesstaat Iowa. Die Forscher wollen die Variablen identifizieren, die den Verkaufspreis beeinflussen. Zu den Variablen gehören die Grundstücksgröße und verschiedene Merkmale der Wohnimmobilie.
Nach der ersten Untersuchung mit CART® Regression zur Identifizierung der wichtigen Prädiktoren verwendet das Team Random Forests® Regression, um ein intensiveres Modell aus demselben Datensatz zu erstellen. Das Team vergleicht die Tabelle mit der Zusammenfassung des Modells und das R2-Diagramm aus den Ergebnissen, um zu bewerten, welches Modell ein besseres Prognoseergebnis liefert.
Diese Daten sind eine Adaption eines öffentlichen Datensatzes, der Informationen zur Wohnsituation in Ames enthält. Originaldaten von DeCock, Truman State University.
- Öffnen Sie die Beispieldaten Ames_Gehause.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antwort die Spalte 'Verkaufspreis' ein.
- Geben Sie in Stetige Prädiktoren'Losfront' – ''Jahr verkauftein.
- Geben Sie in Kategoriale Prädiktoren'Typ' – ''Verkaufsbedingungein.
- Klicken Sie auf Optionen.
- Wählen Sie unter Anzahl der Prädiktoren für die Knotenteilung „K Prozent der Gesamtzahl der Prädiktoren; K =“ und geben Sie 30 ein. Die Forscher möchten für diese Analyse mehr als die Standardanzahl von Prädiktoren verwenden.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
Methode
| Modellvalidierung | Validierung mit Daten von außerhalb des Segments |
|---|---|
| Anzahl der Bootstrap-Stichproben | 300 |
| Stichprobenumfang | Entspricht Umfang der Trainingsdaten von 2930 |
| Anzahl der für die Knotenteilung ausgewählten Prädiktoren | 30% der Gesamtanzahl der Prädiktoren = 23 |
| Minimale interne Knotengröße | 5 |
| Verwendete Zeilen | 2930 |
Informationen zur Antwortvariablen
| Mittelwert | StdAbw | Minimum | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 180796 | 79886,7 | 12789 | 129500 | 160000 | 213500 | 755000 |
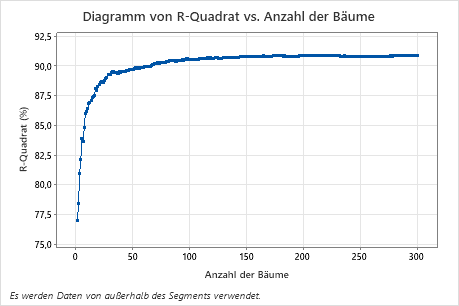
Das Diagramm von R-Quadrat vs. Anzahl der Bäume zeigt die gesamte Kurve über die Anzahl der aufgebauten Bäume. Der R2-Wert steigt mit zunehmender Anzahl der Bäume schnell an und flacht dann um etwa 91% ab.
Zusammenfassung des Modells
| Prädiktoren gesamt | 77 |
|---|---|
| Wichtige Prädiktoren | 68 |
| Statistiken | Außerhalb des Segments |
|---|---|
| R-Quadrat | 90,90% |
| Wurzel des mittleren quadrierten Fehlers (RMSE) | 24097,3281 |
| Mittlerer quadrierter Fehler (MSE) | 5,80681E+08 |
| Mittlere abs. Abweichung (MAD) | 14746,8323 |
| Mittlerer absoluter prozentualer Fehler (MAPE) | 0,0895 |
Die Tabelle mit der Zusammenfassung des Modells zeigt, dass dieR2-Werte gegenüber den R2-Werten der entsprechenden CART®-Analyse leicht verbessert sind.
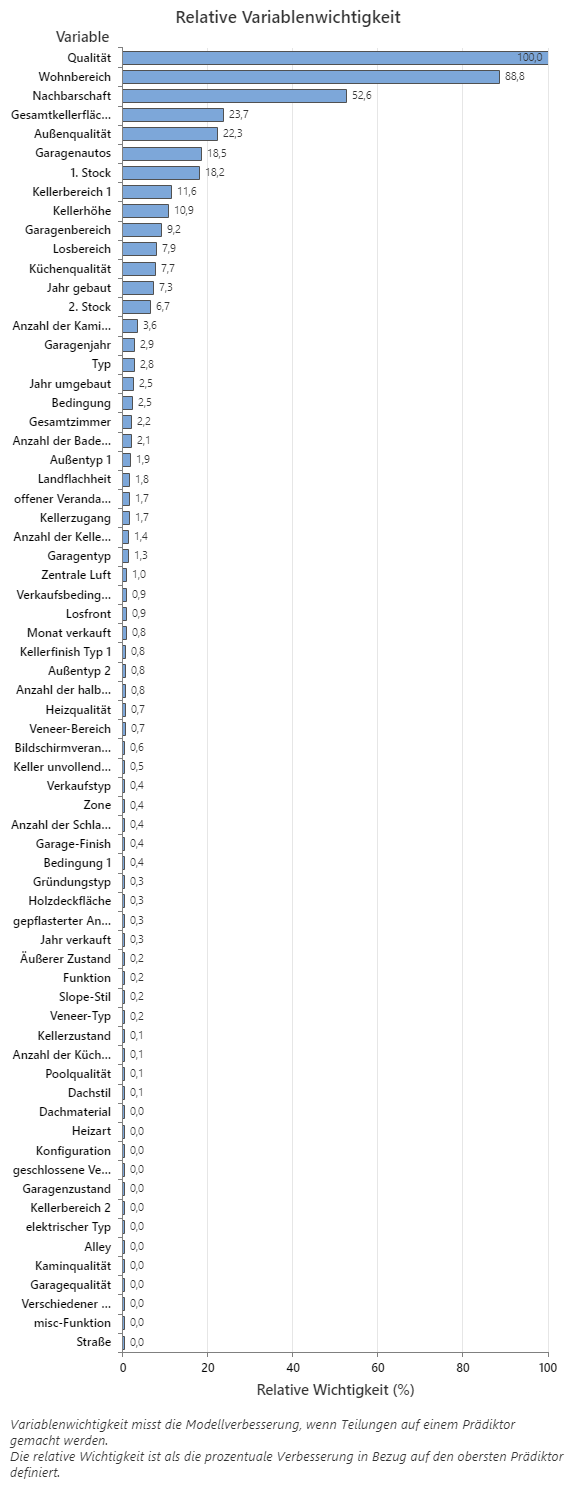
Das Diagramm „Relative Variablenwichtigkeit“ zeigt die Prädiktoren in der Reihenfolge ihrer Auswirkungen auf die Modellverbesserung, wenn Teilungen anhand eines Prädiktors über die Abfolge der Bäume hinweg vorgenommen werden. Die wichtigste Prädiktorvariable für die Prognose des Verkaufspreises ist „Qualität“. Wenn die Wichtigkeit der obersten Prädiktorvariablen, Qualität, 100% beträgt, dann hat die nächste wichtige Variable, Living Area SF, einen Beitrag von 88,8%. Dies bedeutet, dass die Quadratmeterzahl des Wohnzimmers 88,8% so wichtig ist wie die Gesamtqualität der Immobilie. Die zweitwichtigste Variable ist die Nachbarschaft mit einem Beitrag von 52,6%.
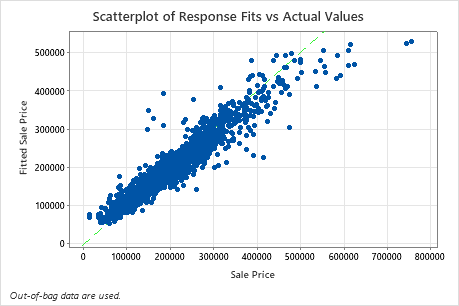
Das Streudiagramm der angepassten Verkaufspreise gegenüber den tatsächlichen Verkaufspreisen zeigt die Beziehung zwischen den angepassten und tatsächlichen Werten für die Daten von außerhalb des Segments. Sie können mit dem Mauszeiger auf die Punkte im Diagramm zeigen, um die dargestellten Werte leichter sehen zu können. In diesem Beispiel fallen viele Punkte ungefähr in die Nähe der Referenzlinie von y=x, aber einige Punkte müssen möglicherweise untersucht werden, um Diskrepanzen zwischen angepassten und tatsächlichen Werten zu sehen.
