Hinweis
Dieser Befehl ist mit Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
Wichtige Variablen
Minitab Statistical Software bietet zwei Methoden, zur Einstufung der Bedeutung der Variablen in eine Rangfolge.
Permutation
- A = 87
- B = 9
- C = 4
Dann beträgt der Abstand für diese Zeile 0,87 – 0,09 = 0,78.
Der durchschnittliche Abstand der Daten von außerhalb des Segments ist der durchschnittliche Abstand für alle Datenzeilen.
Um die Bedeutung der Variablen zu bestimmen, permutieren Sie die Werte einer Variablen xm nach dem Zufallsprinzip durch die Daten von außerhalb des Segments. Lassen Sie die Antwortwerte und die anderen Prädiktorwerte gleich. Verwenden Sie dann die gleichen Schritte zur Berechnung des durchschnittlichen Abstands für die permutierten Daten, 
.
Die Bedeutung für die Variable xm ergibt sich aus der Differenz der beiden Durchschnitte:
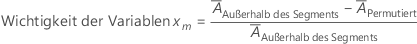
Dabei gilt: 
ist der durchschnittliche Abstand vor der Permutation. Minitab rundet Werte kleiner als 10–7 auf 0.
Gini
Jeder Klassifikationsbaum ist eine Auflistung von Teilungen. Jede Teilung trägt zur Verbesserung des Baums bei.
Mit der folgenden Formel wird die Verbesserung an einem einzelnen Knoten berechnet:
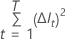
Dabei gilt: 
ist die Anzahl der Knoten, die geteilt werden, und 
für jeden Knoten 
, wobei die Variable von Interesse nicht der Teiler ist.
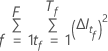
Dabei gilt: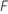 
ist die Anzahl der Bäume im Wald und 
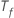ist die Anzahl der Knoten, die im Baum aufgeteilt wurden 
.
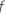Die Berechnung der Knotenverunreinigung ähnelt der Gini-Methode. Weitere Einzelheiten zur Gini-Methode finden Sie unter Knotenteilungsmethoden in CART® Klassifikation.
Durchschnittliche –Log-Likelihood
Daten von außerhalb des Segments
Bei der Berechnung werden Stichproben der Daten von außerhalb des Segments von jedem Baum im Wald verwendet. Aufgrund der Natur von Stichproben der Daten von außerhalb des Segments sollten Sie davon ausgehen, dass Sie verschiedene Kombinationen von Bäumen verwenden, um den Beitrag zur Log-Likelihood für jede Zeile in den Daten zu finden.
Für einen bestimmten Baum im Wald ist eine Klassenabstimmung für eine Zeile in den Daten von außerhalb des Segments die prognostizierte Klasse für die Zeile aus dem einzelnen Baum. Die prognostizierte Klasse für eine Zeile von Daten von außerhalb des Segment ist die Klasse mit der höchsten Stimmenanzahl unter allen Bäumen im Wald. Die prognostizierte Klassenwahrscheinlichkeit für eine Zeile in den Daten von außerhalb des Segments ist das Verhältnis zwischen der Anzahl der Stimmen für die Klasse und den Gesamtstimmen für die Zeile. Die Wahrscheinlichkeitsberechnungen ergeben sich aus diesen Wahrscheinlichkeiten:
Dabei gilt Folgendes:
und 
ist die berechnete Ereigniswahrscheinlichkeit für Zeile i in Daten von außerhalb des Segments.
Notation für Daten von außerhalb des Segments
| Begriff | Beschreibung |
|---|---|
| nAußerhalb des Segments | Anzahl der Zeilen, die mindestens einmal Daten von außerhalb des Segments sind |
| yi, Außerhalb des Segments | binärer Antwortwert von Fall i in den Daten von außerhalb des Segments. yi, Außerhalb des Segments = 1 für Ereignisklasse, sonst 0. |
Testdatensatz
Für einen bestimmten Baum im Wald ist eine Klassenabstimmung für eine Zeile im Testdatensatz die prognostizierte Klasse für die Zeile aus dem einzelnen Baum. Die prognostizierte Klasse für eine Zeile im Testdatensatz ist die Klasse mit der höchsten Stimmenanzahl unter allen Bäumen im Wald. Die prognostizierte Klassenwahrscheinlichkeit für eine Zeile im Testdatensatz ist das Verhältnis zwischen der Anzahl der Stimmen für die Klasse und den Gesamtstimmen für die Zeile. Die Wahrscheinlichkeitsberechnungen ergeben sich aus diesen Wahrscheinlichkeiten:
Dabei gilt Folgendes:
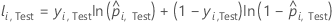
Notation für Testdatensatz
| Begriff | Beschreibung |
|---|---|
| nTest | Stichprobenumfang des Testdatensatzes |
| yi, Test | binärer Antwortwert von Fall i im Testdatensatz. yi, k = 1 für Ereignisklasse, sonst 0. |
<scriptoutputs conref="../scripts/images/mss_interface_callouts_mac.mtb.dita#mss_interface_callouts_mac/all_outputs"/>
 | prognostizierte Ereigniswahrscheinlichkeit für Fall i im Testdatensatz |
Fläche unterhalb der ROC-Kurve
Formel
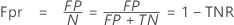
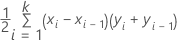
Hierbei ist k die Anzahl der eindeutigen Ereigniswahrscheinlichkeiten und (x0, y0) ist der Punkt (0, 0).
Um die Fläche für eine Kurve anhand von Daten von außerhalb des Segments oder eines Testdatensatzes zu berechnen, verwenden Sie die Punkte aus der entsprechenden Kurve.
Notation
| Begriff | Beschreibung |
|---|---|
| Tpr | Richtig-Positiv-Rate |
| Fpr | Falsch-Positiv-Rate |
| tp | Richtig positiv; Ereignisse, die richtig bewertet wurden |
| fn | falsch negativ, Ereignisse, die falsch bewertet wurden |
| P | Anzahl der tatsächlichen positiven Ereignisse |
| Fp | falsch positiv, Nicht-Ereignisse, die falsch bewertet wurden |
| N | Anzahl der tatsächlichen negativen Ereignisse |
| Fnr | Falsch-Negativ-Rate |
| TNR | Richtig-Negativ-Rate |
Beispiel
| x (Falsch-Positiv-Rate) | y (Richtig-Positiv-Rate) |
|---|---|
| 0,0923 | 0,3051 |
| 0,4154 | 0,7288 |
| 0,7538 | 0,9322 |
| 1 | 1 |
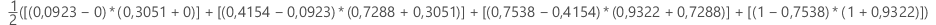
95%-KI für die Fläche unterhalb der ROC-Kurve
Das folgende Intervall gibt die Ober- und die Untergrenze für das Konfidenzintervall an:
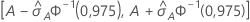
Die Berechnung des Standardfehlers der Fläche unterhalb der ROC-Kurve (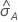
) stammt aus dem Salford Predictive Modeler®. Allgemeine Informationen zum Schätzen der Varianz der Fläche unterhalb ROC-Kurve finden Sie in den folgenden Veröffentlichungen:
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations. In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer. doi:10.1007/978-3-642-16114-8
Cortes, C. and Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305–312.
Feng, D., Cortese, G., und Baumgartner, R. (2017). A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size. Statistical Methods in Medical Research, 26(6), 2603–2621. doi:10.1177/0962280215602040
Notation
| Begriff | Beschreibung |
|---|---|
| A | Fläche unterhalb der ROC-Kurve |
<scriptoutputs conref="../scripts/images/mss_interface_callouts_mac.mtb.dita#mss_interface_callouts_mac/all_outputs"/>
 | 0,975 Perzentil der Standardnormalverteilung |
Lift
Allgemeine Berechnungen für den kumulativen Lift finden Sie unter Methoden und Formeln für das kumulative Lift-Diagramm für Random Forests®-Klassifikation.
Fehlklassifizierungsrate
Die folgende Gleichung ergibt die Fehlklassifizierungsrate:
Die fehlklassifizierte Anzahl ist die Anzahl der Zeilen in den Daten von außerhalb des Segments, in denen sich die prognostizierten Klassen von den wahren Klassen unterscheiden. Die Anzahl gibt die Anzahl der Zeilen in den Daten von außerhalb des Segments an.
Bei der Validierung mit einem Testdatensatz ist die fehlklassifizierte Anzahl die Summe der Fehlklassifizierungen im Testdatensatz. Die Gesamtanzahl ist die Anzahl der Zeilen IN859 im Testdatensatz.
