Hinweis
Dieser Befehl ist mit Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
Verwenden Sie das Gain- und das Lift-Diagramm, um die Leistung Ihres Klassifikationsmodells auszuwerten. Das Gain-Diagramm zeigt die wahre Positiv-Rate in Prozent im Vergleich zum Prozentsatz der Gesamtanzahlen. Das Lift-Diagramm zeigt den kumulativen Lift (oder den nicht kumulativen Lift) im Vergleich zum Prozentsatz der Gesamtanzahlen.
Interpretation des Gain-Diagramms
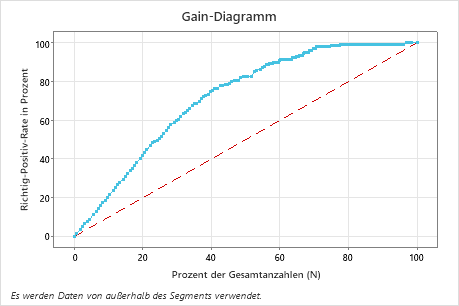
In diesem Beispiel zeigt das Gain-Diagramm einen starken Anstieg über die Referenzlinie und flacht dann ab. In diesem Fall sind rund 40 % der Daten für rund 78% der Richtig-Positiven verantwortlich. Das heißt, wenn ein Unternehmen auf der Grundlage des Modells die entsprechenden 20 % der Bevölkerung anvisiert, beträgt die Richtig-Positiv-Rate etwa 40 %. Ohne das Modell beträgt der entsprechende Prozentsatz 20 %. Diese Differenz entspricht dem zusätzlichen Gain, der aus der Verwendung des Modells resultiert.
Interpretation des Lift-Diagramms
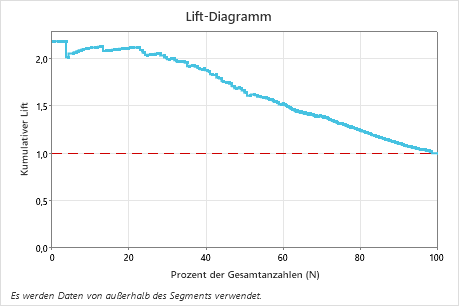
In diesem Beispiel zeigt das Lift-Diagramm einen starken Anstieg über die Referenzlinie und fällt dann ab. Wenn wir also mit diesem Modell die 10 % der Kunden mit den höchsten prognostizierten Antwortwahrscheinlichkeiten kontaktieren, erwarten wir mehr als doppelt so viele Antworten, wie wir erwarten würden, wenn wir 10 % der Kunden zufällig kontaktieren würden.
