Hinweis
Dieser Befehl ist mit dem Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
MARS®-Regression Erstellt im Wesentlichen flexible Modelle durch Anpassung stückweiser linearer Regressionen. Das Modell hat die Einschränkung, dass sich die Endpunkte der stückweisen Linien gleichmäßig verbinden. Approximationen der Nichtlinearität der Modelle verwenden separate Regressionssteigungen in unterschiedlichen Intervallen der Daten. Eine Annäherung an den Prozess ist im einfachen, 2-dimensionalen Fall leicht zu visualisieren.
Im 2-dimensionalen Fall passt eine einzelne, gerade Linie zu den Daten. Dieses Modell bietet eine Grundlage für das Testen der Verbesserung durch Hinzufügen zusätzlicher Komplexität.
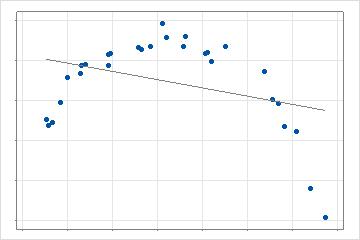
Im nächsten Schritt sucht die Analyse nach dem Wert eines Prädiktors, der eine Basisfunktion erzeugt, die zur größten Verbesserung des Suchkriteriums führt. Die Berechnung des Kriteriums hängt von der Auswahl für die Analyse und von der Validierungsmethode ab. Im 2-dimensionalen Fall ist dieses Modell eine stückweise, lineare Regression mit 2 Linien anstelle von 1 Linie. Bei mehreren Prädiktoren wertet die Suche nach dem besten Datenpunkt jeden Prädiktor aus, den die Analyse zulässt.
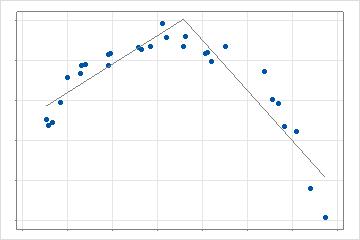
Nachdem die Analyse den ersten Wert gefunden hat, der die beste Verbesserung bietet, durchsucht die Analyse die verbleibenden Prädiktorwerte, um die beste Verbesserung gegenüber dem aktuellen Modell zu finden. Im 2-dimensionalen Fall hat dieses Modell 3 Linien, die verschiedene Teile der Daten beschreiben. Die Suche wiederholt sich bis zur maximalen Anzahl von Basisfunktionen für die Analyse. Wenn Interaktionen zulässig sind, führt die Analyse zusätzliche Suchreihen durch, indem die Kandidatenbasisfunktionen mit anderen Basisfunktionen multipliziert werden, die bereits im Modell vorhanden sind.
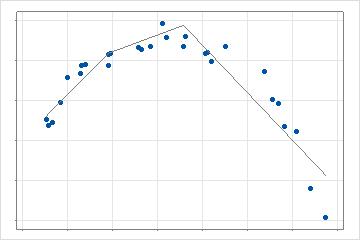
Nachdem die Analyse schnell die maximale Anzahl von Basisfunktionen angepasst und die Parameter dieser Funktionen geschätzt hat, identifiziert die Analyse die optimale Anzahl von Basisfunktionen. Die optimale Anzahl von Basisfunktionen verwendet einen schrittweisen, rückwärts eliminierten Ansatz, um die Anzahl der Basisfunktionen mit dem besten Wert des Optimalitätskriteriums zu finden.
Fehlende Werte für die Modellanpassung
Erstellt bei der Suche nach den Basisfunktionen MARS®-Regression Indikatorvariablen für beliebige Prädiktoren mit fehlenden Werten. Die Indikatorvariable zeigt an, ob ein Wert des Prädiktors fehlt. Wenn die Analyse eine Basisfunktion für einen Prädiktor mit fehlenden Werten im Modell enthält, enthält das Modell auch eine Basisfunktion für die Indikatorvariable. Die anderen Basisfunktionen für den Prädiktor interagieren alle mit der Basisfunktion für die Indikatorvariable.
Wenn ein Prädiktor einen fehlenden Wert aufweist, macht die Basisfunktion für die Indikatorvariable die anderen Basisfunktionen für diesen Prädiktor durch Multiplikation mit 0 zunichte. Diese Basisfunktionen für fehlende Werte sind in allen Modellen enthalten, in denen wichtige Prädiktoren fehlende Werte haben, sogar in additiven Modellen und Modellen, die andere Arten von Transformationen deaktivieren.
Fehlende Werte für die Vorhersage
MARS®-Regression Berechnet Vorhersagen, wenn Prädiktoren im Modell fehlende Werte aufweisen. Bei der Analyse werden unterschiedliche Strategien verwendet, je nachdem, ob fehlende Werte für den Prädiktor vorhanden waren, als die Analyse in das Modell passte. Wenn fehlende Werte für den Prädiktor vorhanden waren, als die Analyse in das Modell passte, enthalten die Basisfunktionen im Modell eine Indikatorvariable, die den Prädiktor aus dem Modell entfernt, wenn der Prädiktor einen fehlenden Wert aufweist.
Der zweite Fall ist, wenn die Werte für die Vorhersage fehlende Werte für einen Prädiktor enthalten, der Prädiktor jedoch keine fehlenden Werte hatte, als die Analyse in das Modell passte. Um in diesem Fall Vorhersagen zu berechnen, unterschreibt die Analyse den fehlenden Wert. Bei einem kontinuierlichen Prädiktor ersetzt der Mittelwert des Prädiktors den fehlenden Wert. Bei einem kategorialen Prädiktor ersetzt der letzte nicht fehlende Wert im Datensatz den fehlenden Wert.
