Hinweis
Dieser Befehl ist mit Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
y = b0 + b 1BF1 + b 2 BF2 +... + bk BFk
- y ist die Antwortvariable.
- b0 ist der konstante Term
- B1 + B2 + ... + bk sind Koeffizienten für die Basisfunktionen
- BF1 + BF2 + ... + BFk sind die Basisfunktionen
Lösen Sie die Basisfunktionen für Werte des Prädiktors, um den vorhergesagten Wert der Antwort zu berechnen.
Basisfunktionen
- max(0, X − c)
- Positiver Koeffizient
- Der Beitrag ist 0 bis c und erhöht sich dann.
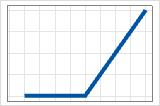
- max(0, X − c)
- Negativer Koeffizient
- Der Beitrag ist das Maximum bis c, dann sinkt er.
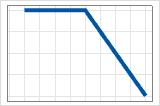
- max(0, c − X)
- Positiver Koeffizient
- Der Beitrag beginnt maximal und sinkt bis c. Nach c ist der Beitrag 0.
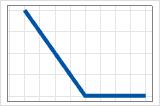
- max(0, c − X)
- Negativer Koeffizient
- Der Beitrag beginnt bei 0 und steigt bis c. Nach c sind die Beiträge auf dem Maximalwert.
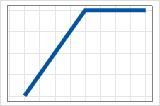
Wenn c gleich dem minimalen oder maximalen Wert des Prädiktors ist, dann hat der Prädiktor für alle Werte der Basisfunktion den gleichen Effekt. Das partielle Abhängigkeitsdiagramm für diese 2 Fälle zeigt eine gerade Linie. MARS®-Regression macht C zu einem der Endpunkte in einer Analyse, die Transformationen für den Prädiktor nicht zulässt.
Für kategoriale Prädiktoren sind Basisfunktionen Indikatorfunktionen. Die Funktion hat für einige Kategorien den Wert 0 und für die anderen Kategorien den Wert 1. Die Basisfunktionen haben folgende Form:
Wenn X x1ist, ... xk wobei k die Anzahl der Ebenen in der Basisfunktion ist, k ≥ 1.
Der Wert der Funktion ist 1 für die Kategorien in der Basisfunktion. Die Multiplikation der Basisfunktion mit dem Koeffizienten in der Regressionsgleichung bestimmt den Effekt, wenn die Funktion von 0 auf 1 wechselt.
Beispiel für einen stetigen Prädiktor in 1 Basisfunktion
In diesen Ergebnissen hat BF2 einen negativen Koeffizienten in der Regressionsgleichung. Der Koeffizient für die Basisfunktion ist −57,6167. Die Anordnung der Basisfunktion ist max(0, c − X). In dieser Anordnung nimmt der Wert der Basisfunktion ab, wenn der Prädiktor zunimmt. Die Kombination dieser Anordnung und des negativen Koeffizienten erzeugt eine positive Beziehung zwischen der Prädiktorvariablen und der Antwortvariablen. Der Effekt Wohnbereich von soll in der Region von 438 auf 3.078 steigen Verkaufspreis . Die Steigung von ist 57.6167 von Wohnbereich 438 bis 3,078.
Regressionsgleichung
BF3 = wenn Qualität gleich 8; 9; 10
BF6 = max(0, 2002 - Jahr gebaut)
BF7 = wenn Kellerbereich 1 nicht fehlt
BF10 = max(0, 1696 - Kellerbereich 1) * BF7
BF11 = wenn Qualität gleich 1; 8
BF13 = wenn Typ gleich 90; 150; 160; 180; 190
BF15 = wenn Nachbarschaft gleich Blaustem; Clear Creek; Crawford; Grüne Hügel; Landmark;
Northridge; Northridge Heights; Somerset Villages; Steinbrücke; Timberland; Veenker
BF17 = wenn Gesamtkellerfläche nicht fehlt
BF19 = max(0, Gesamtkellerfläche - 1392) * BF17
BF21 = max(0, 1. Stock - 2402)
BF23 = wenn Bedingung gleich 1; 2; 3; 4; 5; 6
BF25 = wenn Qualität gleich 1; 7; 10
BF27 = max(0, 1. Stock - 2207)
BF30 = max(0, 15138 - Losbereich)
Verkaufspreis = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Ein Diagramm der partiellen Abhängigkeit eines Prädiktors
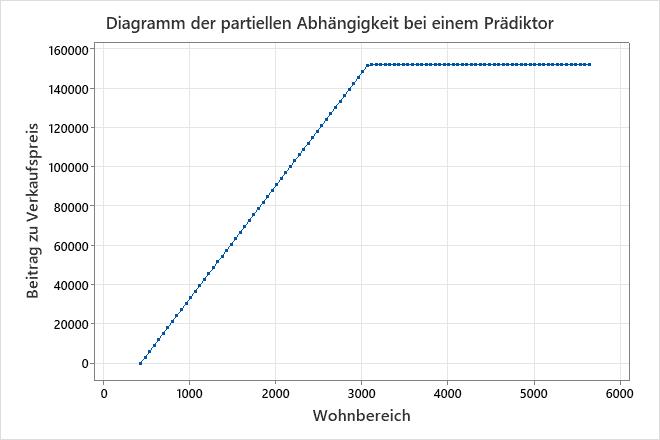
Verwenden Sie in einem additiven Modell die Diagramme für partielle Abhängigkeit mit einem Prädiktor, um einen Einblick in die Auswirkungen der wichtigen kontinuierlichen Prädiktoren auf die vorhergesagte Antwort zu erhalten. Das Diagramm der partiellen Abhängigkeit bei einem Prädiktor gibt an, wie sich die Antwort variablen Änderungen bei den Prädiktorebenen voraussichtlich ändert. Für MARS®-Regressionstammen die Werte im Diagramm aus den Basisfunktionen für den Prädiktor auf der x-Achse. Der Beitrag auf der y-Achse ist standardisiert, so dass der Mindestwert auf dem Diagramm 0 ist.
Dieses Diagramm veranschaulicht, dass dies zunimmt, Verkaufspreis wenn die Wohnbereich minimale Quadratmeterzahl im Datensatz auf etwa 3.000 Quadratfuß steigt. Nach Wohnbereich dem Erreichen von 3.000 Quadratfuß wird der Beitrag Verkaufspreis bei etwa 152.000 US-Dollar flach.
Beispiel für einen kategorialen Prädiktor in 1 Basisfunktion
In diesen Ergebnissen ist BF3 für den Prädiktor Qualität. Die Basisfunktion ist für den Fall, dass der Wert von Qualität 8, 9 oder 10 ist. Der Koeffizient für BF3 in der Gleichung beträgt 115.438. Diese Basisfunktion gibt an, dass, wenn sich der Wert der Qualität von einem Wert von 1 bis 7 auf einen Wert von 8, 9 oder 10 ändert, der Verkaufspreis im Modell um 115.438 USD steigt. Qualität ist auch in BF11 und BF25. Um die Auswirkung des Prädiktors auf die Antwortvariable zu verstehen, betrachten Sie alle Basisfunktionen.
Regressionsgleichung
BF3 = wenn Qualität gleich 8; 9; 10
BF6 = max(0, 2002 - Jahr gebaut)
BF7 = wenn Kellerbereich 1 nicht fehlt
BF10 = max(0, 1696 - Kellerbereich 1) * BF7
BF11 = wenn Qualität gleich 1; 8
BF13 = wenn Typ gleich 90; 150; 160; 180; 190
BF15 = wenn Nachbarschaft gleich Blaustem; Clear Creek; Crawford; Grüne Hügel; Landmark;
Northridge; Northridge Heights; Somerset Villages; Steinbrücke; Timberland; Veenker
BF17 = wenn Gesamtkellerfläche nicht fehlt
BF19 = max(0, Gesamtkellerfläche - 1392) * BF17
BF21 = max(0, 1. Stock - 2402)
BF23 = wenn Bedingung gleich 1; 2; 3; 4; 5; 6
BF25 = wenn Qualität gleich 1; 7; 10
BF27 = max(0, 1. Stock - 2207)
BF30 = max(0, 15138 - Losbereich)
Verkaufspreis = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Hinweis
In einer herkömmlichen Regressionsgleichung stellt der Koeffizient in der Regressionsgleichung immer die Änderung von 0 nach 1 dar. In MARS®-Regressionkann der Koeffizient die Änderung von 1 bis 0 darstellen. Betrachten Sie eine binäre kategoriale Variable, die 0 ist, wenn ein Patient berichtet, dass er keine Kopfschmerzen hat, und 1, wenn ein Patient berichtet, dass er Kopfschmerzen hat. Angenommen, der Prädiktor hat die folgende Basisfunktion:
- BF1 = wenn Kopfschmerzen 0 sind
Mehrere Basisfunktionen für 1 Prädiktor
MARS®-Regression Verwendet mehrere Basisfunktionen für einen einzelnen Prädiktor, um komplexere nichtlineare Beziehungen zwischen einem Prädiktor und der Antwortvariablen zu modellieren. Zusätzliche Basisfunktionen erzeugen zusätzliche Änderungen in der Steigung der Beziehung zwischen dem Prädiktor und der Antwortvariablen. MARS®-Regression Ermöglicht Prädiktoren in mehreren Basisfunktionen in additiven Modellen.
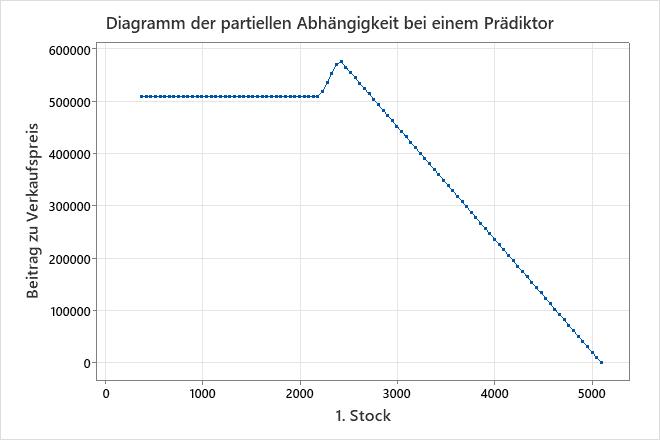
In diesen Ergebnissen ist BF21 für den Prädiktor 1. Stock. Die Basisfunktion BF27 ist ebenfalls für 1. Stock. BF21 und BF27 haben beide die gleiche Anordnung, max(0, X − c). Basisfunktionen in dieser Anordnung wirken sich auf die Antwortvariable aus, wenn der Prädiktor einen Wert größer als c hat. Bei 2 Basisfunktionen mit dieser Anordnung wirkt sich keine Basisfunktion auf die Antwortvariablen aus, bis der Prädiktor den Mindestwert in 1 der Basisfunktionen erreicht. In diesen Ergebnissen beträgt dieser Wert 2.207 in BF27. 1. Stock hat eine Steigung von 0 vom Mindestwert bis 2.207. Nach 2.207 gilt die Steigung von BF27, woraus sich eine Steigung von 361,254 ergibt. Diese Steigung bleibt bestehen, bis der Prädiktor die Konstante in BF21 erreicht, woraufhin die Koeffizienten von BF27 und BF21 beeinflussen Verkaufspreis. Die Summe der beiden Koeffizienten ergibt die neue Steigung, 361,254 + (−576,789) = −215,535. Zeigt in einem additiven Modell ein Diagramm mit einem Prädiktor und teilweiser MARS®-Regression Abhängigkeit an, um die Wirkung des Prädiktors anzuzeigen.
Regressionsgleichung
BF3 = wenn Qualität gleich 8; 9; 10
BF6 = max(0, 2002 - Jahr gebaut)
BF7 = wenn Kellerbereich 1 nicht fehlt
BF10 = max(0, 1696 - Kellerbereich 1) * BF7
BF11 = wenn Qualität gleich 1; 8
BF13 = wenn Typ gleich 90; 150; 160; 180; 190
BF15 = wenn Nachbarschaft gleich Blaustem; Clear Creek; Crawford; Grüne Hügel; Landmark;
Northridge; Northridge Heights; Somerset Villages; Steinbrücke; Timberland; Veenker
BF17 = wenn Gesamtkellerfläche nicht fehlt
BF19 = max(0, Gesamtkellerfläche - 1392) * BF17
BF21 = max(0, 1. Stock - 2402)
BF23 = wenn Bedingung gleich 1; 2; 3; 4; 5; 6
BF25 = wenn Qualität gleich 1; 7; 10
BF27 = max(0, 1. Stock - 2207)
BF30 = max(0, 15138 - Losbereich)
Verkaufspreis = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Basisfunktionen für fehlende Werte
Erstellt bei der Suche nach den Basisfunktionen MARS®-Regression Indikatorvariablen für beliebige Prädiktoren mit fehlenden Werten. Die Indikatorvariable zeigt an, ob ein Wert des Prädiktors fehlt. Wenn die Analyse eine Basisfunktion für einen Prädiktor mit fehlenden Werten im Modell enthält, enthält das Modell auch eine Basisfunktion für die Indikatorvariable. Die anderen Basisfunktionen für den Prädiktor interagieren alle mit der Basisfunktion für die Indikatorvariable.
Wenn ein Prädiktor einen fehlenden Wert aufweist, macht die Basisfunktion für die Indikatorvariable die anderen Basisfunktionen für diesen Prädiktor durch Multiplikation mit 0 zunichte. Diese Basisfunktionen für fehlende Werte sind in allen Modellen enthalten, in denen wichtige Prädiktoren fehlende Werte haben, sogar in additiven Modellen und Modellen, die andere Arten von Transformationen deaktivieren.
In diesen Ergebnissen ist BF7 für den Prädiktor Kellerbereich 1. BF 7 hat den Wert 1, wenn Kellerbereich 1 es in den Daten enthalten ist. BF 7 hat den Wert 0, wenn Kellerbereich 1 er fehlt. BF7 ist in der Regressionsgleichung nicht vorhanden, da die Basisfunktion im endgültigen Modell nicht wichtig war, aber BF7 interagiert mit BF10. BF10 ist wichtig und in der Regressionsgleichung vorhanden. Der Effekt von BF7 besteht darin, BF10 mit 0 zu multiplizieren, wenn er fehlt, wodurch der Effekt entfernt wird, wenn Kellerbereich 1 Kellerbereich 1 er fehlt.
Regressionsgleichung
BF3 = wenn Qualität gleich 8; 9; 10
BF6 = max(0, 2002 - Jahr gebaut)
BF7 = wenn Kellerbereich 1 nicht fehlt
BF10 = max(0, 1696 - Kellerbereich 1) * BF7
BF11 = wenn Qualität gleich 1; 8
BF13 = wenn Typ gleich 90; 150; 160; 180; 190
BF15 = wenn Nachbarschaft gleich Blaustem; Clear Creek; Crawford; Grüne Hügel; Landmark;
Northridge; Northridge Heights; Somerset Villages; Steinbrücke; Timberland; Veenker
BF17 = wenn Gesamtkellerfläche nicht fehlt
BF19 = max(0, Gesamtkellerfläche - 1392) * BF17
BF21 = max(0, 1. Stock - 2402)
BF23 = wenn Bedingung gleich 1; 2; 3; 4; 5; 6
BF25 = wenn Qualität gleich 1; 7; 10
BF27 = max(0, 1. Stock - 2207)
BF30 = max(0, 15138 - Losbereich)
Verkaufspreis = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Basisfunktionen für Interaktionen
Um Interaktionen zu modellieren, MARS®-Regression multipliziert Basisfunktionen für verschiedene Prädiktoren. MARS®-Regression Berücksichtigt keine Wechselwirkungen im additiven Standardmodell. Partielle Abhängigkeitsdiagramme sind für eine Analyse, die Wechselwirkungen berücksichtigt, nicht verfügbar.
Eine Wechselwirkung bedeutet, dass die Wirkung eines Prädiktors vom Wert anderer Prädiktoren abhängt. Zum Beispiel hängt die Geschwindigkeit, mit der Getreide in einem Ofen trocknet, von der Zeit im Ofen ab, aber die Wirkung der Zeit hängt von der Temperatur des Ofens ab. Die Zeit- und Temperaturvariablen interagieren.
In den Ergebnissen für ein Modell mit Wechselwirkungen ist BF9 für den Prädiktor Qualität. BF12 ist für den Prädiktor 1. Stock. Die Berechnung von BF12 beinhaltet die Multiplikation mit BF9, so dass die beiden Prädiktoren interagieren. Bestimmung der Wirkung oder Qualität 1. Stock erfordert Kenntnis des Wertes des anderen Prädiktors. Der Koeffizient für BF12 von −63,1685 gilt nur, wenn der Wert von BF9 1 ist. Der Wert von BF9 ist 1, wenn Qualität 8, 9 oder 10 ist. Aufgrund der Anordnung von BF12, 1. Stock hat eine Steigung von 63,1685, wenn die Quadratmeterzahl weniger als 2.470 ist und der Wert von Qualität 8, 9 oder 10 ist.
Regressionsgleichung
BF4 = max(0, 2002 - Jahr gebaut)
BF5 = wenn Kellerbereich 1 nicht fehlt
BF7 = max(0, Kellerbereich 1 - 1758) * BF5
BF8 = max(0, 1758 - Kellerbereich 1) * BF5
BF9 = wenn Qualität gleich 8; 9; 10
BF12 = max(0, 2470 - 1. Stock) * BF9
BF14 = wenn Qualität gleich 7; 9; 10
BF15 = wenn Typ gleich 75; 90; 150; 160; 180; 190
BF19 = wenn Nachbarschaft gleich Blaustem; Clear Creek; Crawford; Grüne; Grüne Hügel;
Northridge; Northridge Heights; Somerset Villages; Steinbrücke; Timberland; Veenker * BF5
BF21 = wenn Bedingung gleich 1; 2; 3; 4; 5; 6 * BF4
BF25 = max(0, 1. Stock - 372) * BF7
BF26 = wenn Gesamtkellerfläche nicht fehlt * BF14
BF28 = max(0, Gesamtkellerfläche - 689) * BF26
Verkaufspreis = 320349 - 66,4387 * BF2 - 28,2065 * BF8 + 123645 * BF9 - 63,1685 * BF12 -
23751,7 * BF15 + 22818,2 * BF19 - 523,924 * BF21 - 0,036887 * BF25 + 53,9878 * BF28
