Um zu ermitteln, wie gut das Modell an die Daten angepasst ist, untersuchen Sie die Statistiken in der Tabelle „Zusammenfassung des Modells“.
Prädiktoren gesamt
Die Anzahl der insgesamt für das Modell verfügbaren Prädiktoren. Dies ist die Summe der angegebenen stetigen und kategorialen Prädiktoren.
Wichtige Prädiktoren
Die Anzahl der wichtigen Prädiktoren im Modell. Wichtige Prädiktoren sind die Variablen, die mindestens 1 Basisfunktion im Modell haben.
Interpretation
Mit dem Diagramm „Relative Variablenwichtigkeit“ können Sie die Rangfolge der relativen Variablenwichtigkeit anzeigen. Angenommen, 10 von 20 Prädiktoren haben Basisfunktionen im Modell, zeigt das Diagramm "Relative Variablenwichtigkeit" die Variablen in der Reihenfolge der Wichtigkeit an.
Maximale Anzahl von Basisfunktionen
Die Anzahl der Basisfunktionen, die der Algorithmus erstellt, um nach dem optimalen Modell zu suchen.
Interpretation
Standardmäßig legt die Minitab-Statistiksoftware die maximale Anzahl von Basisfunktionen auf 30 fest. Ziehen Sie einen größeren Wert in Betracht, wenn 30 Basisfunktionen für die Daten zu klein erscheinen. Betrachten Sie beispielsweise einen größeren Wert, wenn Sie der Meinung sind, dass mehr als 30 Prädiktoren wichtig sind.
Optimale Anzahl von Basisfunktionen
Die Anzahl der Basisfunktionen im optimalen Modell.
Interpretation
Nachdem die Analyse das Modell mit der maximalen Anzahl von Basisfunktionen geschätzt hat, verwendet die Analyse ein Rückwärtseliminierungsverfahren, um Basisfunktionen aus dem Modell zu entfernen. Die Analyse entfernt nacheinander die Basisfunktion, die am wenigsten zur Modellanpassung beiträgt. Bei jedem Schritt berechnet die Analyse den Wert des Optimalitätskriteriums für die Analyse, entweder R-Quadrat oder mittlere absolute Abweichung. Nach Abschluss des Eliminierungsverfahrens ist die optimale Anzahl von Basisfunktionen die Anzahl aus dem Eliminierungsverfahren, die den optimalen Wert des Kriteriums ergibt.
R-Quadrat
R2 ist der Prozentsatz der Streuung in der Antwortvariablen, den das Modell erklärt. Ausreißer haben eine größere Auswirkung auf das R2 als auf die MAD und den MAPE.
Wenn Sie eine Validierungsmethode verwenden, enthält die Tabelle das R2 für den Trainingsdatensatz und das R2 für den Testdatensatz. Wenn die Validierungsmethode die Kreuzvalidierung mit K Faltungen ist, entspricht der Testdatensatz jeder Faltung, wenn diese Faltung bei der Modellerstellung ausgeschlossen wird. Das R2 für den Test ist im Allgemeinen ein besseres Maß für die Eignung des Modells für neue Daten.
Interpretation
Verwenden Sie das R2, um zu bestimmen, wie gut das Modell für Ihre Daten passend ist. Je höher das R2, desto besser ist das Modell für Ihre Daten passend. R2 liegt immer zwischen 0% und 100%.
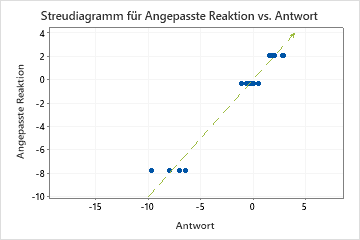
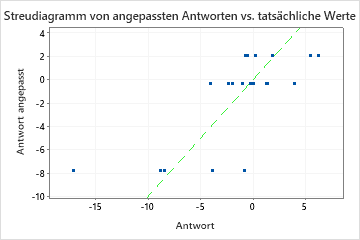
Ein R2 für den Test, das erheblich kleiner als das R2 für das Training ist, deutet darauf hin, dass das Modell möglicherweise besser für den aktuellen Datensatz passend ist als es die Werte der Antwortvariablen für neue Fälle prognostizieren kann.
Wurzel des mittleren quadrierten Fehlers (RMSE)
Die Wurzel des mittleren quadrierten Fehlers (RMSE) ist ein Maß für die Genauigkeit des Modells. Ausreißer haben eine größere Auswirkung auf die RMSE als auf die MAD und den MAPE.
Wenn Sie eine Validierungsmethode verwenden, enthält die Tabelle eine RMSE für den Trainingsdatensatz und eine RMSE für den Testdatensatz. Wenn die Validierungsmethode die Kreuzvalidierung mit K Faltungen ist, entspricht der Testdatensatz jeder Faltung, wenn diese Faltung bei der Modellerstellung ausgeschlossen wird. Die RMSE für den Test ist im Allgemeinen ein besseres Maß für die Eignung des Modells für neue Daten.
Interpretation
Hiermit können Sie die Anpassungen verschiedener Modelle vergleichen. Kleinere Werte weisen auf eine bessere Anpassung hin. Eine RMSE für den Test, die erheblich kleiner als die RMSE für das Training ist, deutet darauf hin, dass das Modell möglicherweise besser für den aktuellen Datensatz passend ist als es die Werte der Antwortvariablen für neue Fälle prognostizieren kann.
Mittlerer quadrierter Fehler (MSE)
Der mittlere quadrierte Fehler (MSE) ist ein Maß für die Genauigkeit des Modells. Ausreißer haben eine größere Auswirkung auf den MSE als auf die MAD und den MAPE.
Wenn Sie eine Validierungsmethode verwenden, enthält die Tabelle einen MSE für den Trainingsdatensatz und einen MSE für den Testdatensatz. Wenn die Validierungsmethode die Kreuzvalidierung mit K Faltungen ist, entspricht der Testdatensatz jeder Faltung, wenn diese Faltung bei der Modellerstellung ausgeschlossen wird. Der MSE für den Test ist im Allgemeinen ein besseres Maß für die Eignung des Modells für neue Daten.
Interpretation
Hiermit können Sie die Anpassungen verschiedener Modelle vergleichen. Kleinere Werte weisen auf eine bessere Anpassung hin. Ein MSE für den Test, der erheblich kleiner als der MSE für das Training ist, deutet darauf hin, dass das Modell möglicherweise besser für den aktuellen Datensatz passend ist als es die Werte der Antwortvariablen für neue Fälle prognostizieren kann.
Mittlere absolute Abweichung (MAD)
Die mittlere absolute Abweichung (MAD) drückt die Genauigkeit in der gleichen Einheit wie die Daten aus. Auf diese Weise kann der Fehleranteil leichter erfasst werden. Ausreißer haben eine geringere Auswirkung auf die MAD als auf das R2, die RMSE und den MSE.
Wenn Sie eine Validierungsmethode verwenden, enthält die Tabelle eine MAD für den Trainingsdatensatz und eine MAD für den Testdatensatz. Wenn die Validierungsmethode die Kreuzvalidierung mit K Faltungen ist, entspricht der Testdatensatz jeder Faltung, wenn diese Faltung bei der Modellerstellung ausgeschlossen wird. Der MAD für den Test ist im Allgemeinen ein besseres Maß für die Eignung des Modells für neue Daten.
Interpretation
Hiermit können Sie die Anpassungen verschiedener Modelle vergleichen. Kleinere Werte weisen auf eine bessere Anpassung hin. Ein MAD für den Test, der erheblich kleiner als der MAD für das Training ist, deutet darauf hin, dass das Modell möglicherweise besser für den aktuellen Datensatz passend ist als es die Werte der Antwortvariablen für neue Fälle prognostizieren kann.
