Hinweis
Dieser Befehl ist mit Predictive Analytics-Modul verfügbar. Klicken Sie hier, um weitere Informationen zum Aktivieren des Moduls zu erhalten.
Ein Forscherteam sammelt Daten aus dem Verkauf einzelner Wohnimmobilien in Ames im US-Bundesstaat Iowa. Die Forscher wollen die Variablen identifizieren, die den Verkaufspreis beeinflussen. Zu den Variablen gehören die Grundstücksgröße und verschiedene Merkmale der Wohnimmobilie. Die Forscher wollen beurteilen, wie gut das beste MARS-Modell® zu den Daten passt.
- Öffnen Sie die Beispieldaten Ames_Gehause.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antwort die Spalte 'Verkaufspreis' ein.
- Geben Sie in Stetige Prädiktoren'Losfront' – ''Jahr verkauftein.
- Geben Sie Typ in Kategoriale Prädiktorenein: 'Verkaufsbedingung'.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
Standardmäßig passt ein additives Modell, MARS®-Regression sodass alle Basisfunktionen in der Regressionsgleichung 1 Prädiktor verwenden. Der erste Prädiktor in der Liste ist BF2. BF2 verwendet den Prädiktor Wohnbereich. Da sich der Prädiktor in der Basisfunktion 1 befindet, hat der Prädiktor 2 verschiedene Steigungen im Modell. Die Funktion max(0, 3078 - Wohnbereich) definiert, dass die Steigung ungleich Null ist, wenn die Wohnfläche kleiner als 3.078 ist.
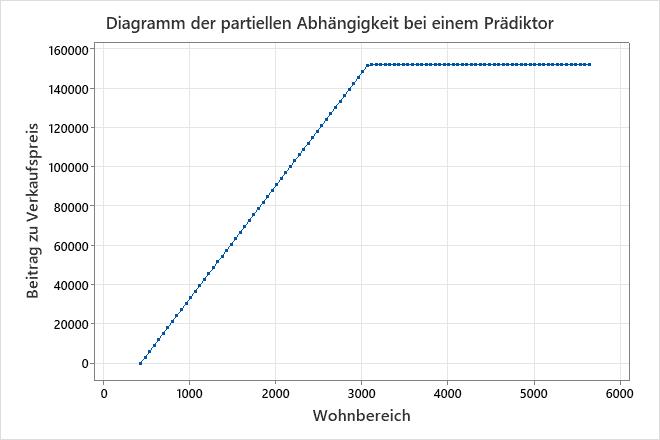
Die Ergebnisse für ein additives Modell umfassen partielle Abhängigkeitsdiagramme für kontinuierliche Prädiktoren, die im Modell wichtig sind. Verwenden Sie das Diagramm, um die Auswirkungen aller Basisfunktionen für einen Prädiktor im gesamten Prädiktorbereich anzuzeigen. In diesen Ergebnissen zeigt das partielle Abhängigkeitsdiagramm, dass bei einem Wert von Wohnbereich 438 bis 3.078 die Steigung etwa 57,6 beträgt. Wenn Wohnbereich größer als 3.078 ist, ist die Steigung 0.
In diesen Ergebnissen hat BF2 einen negativen Koeffizienten in der Regressionsgleichung. Die Anordnung der Basisfunktion ist max(0, c − X). In dieser Anordnung nimmt der Wert der Basisfunktion ab, wenn der Prädiktor zunimmt. Die Kombination dieser Anordnung und des negativen Koeffizienten erzeugt eine positive Beziehung zwischen der Prädiktorvariablen und der Antwortvariablen. Der Effekt Wohnbereich von soll in der Region von 438 auf 3.078 steigen Verkaufspreis .
Die Analyse umfasst auch kategoriale Prädiktoren. Zum Beispiel ist BF3 für den Prädiktor Qualität. Die Basisfunktion ist für den Fall, dass der Wert von Qualität 8, 9 oder 10 ist. Der Koeffizient für BF3 in der Gleichung beträgt 115.438. Diese Basisfunktion gibt an, dass, wenn sich der Wert der Qualität von einem Wert von 1 bis 7 auf einen Wert von 8, 9 oder 10 ändert, der Verkaufspreis im Modell um 115.438 USD steigt. Qualität ist auch in BF11 und BF25. Um die Auswirkung des Prädiktors auf die Antwortvariable zu verstehen, betrachten Sie alle Basisfunktionen.
Zwei der Prädiktoren, die im Modell wichtig sind, haben fehlende Werte in den Trainingsdaten: Kellerbereich 1 und Gesamtkellerfläche. Die Liste der Basisfunktionen enthält Basisfunktionen, die identifizieren, wenn diese Prädiktoren fehlen: BF7 und BF17. Wenn ein Prädiktor einen fehlenden Wert aufweist, macht die Basisfunktion für die Indikatorvariable die anderen Basisfunktionen für diesen Prädiktor durch Multiplikation mit 0 zunichte.
Regressionsgleichung
BF3 = wenn Qualität gleich 8; 9; 10
BF6 = max(0, 2002 - Jahr gebaut)
BF7 = wenn Kellerbereich 1 nicht fehlt
BF10 = max(0, 1696 - Kellerbereich 1) * BF7
BF11 = wenn Qualität gleich 1; 8
BF13 = wenn Typ gleich 90; 150; 160; 180; 190
BF15 = wenn Nachbarschaft gleich Blaustem; Clear Creek; Crawford; Grüne Hügel; Landmark;
Northridge; Northridge Heights; Somerset Villages; Steinbrücke; Timberland; Veenker
BF17 = wenn Gesamtkellerfläche nicht fehlt
BF19 = max(0, Gesamtkellerfläche - 1392) * BF17
BF21 = max(0, 1. Stock - 2402)
BF23 = wenn Bedingung gleich 1; 2; 3; 4; 5; 6
BF25 = wenn Qualität gleich 1; 7; 10
BF27 = max(0, 1. Stock - 2207)
BF30 = max(0, 15138 - Losbereich)
Verkaufspreis = 325577 - 57,6167 * BF2 + 115438 * BF3 - 605,079 * BF6 - 25,3989 * BF10 -
66735,2 * BF11 - 23688,9 * BF13 + 22374,5 * BF15 + 50,3801 * BF19 - 576,789 * BF21 - 18099,2
* BF23 + 22414,2 * BF25 + 361,254 * BF27 - 1,82 * BF30
Hinweis
In diesen Ergebnissen hat die Liste der Basisfunktionen 15 Basisfunktionen, aber die optimale Anzahl von Basisfunktionen ist 13. Die Regressionsgleichung enthält 13 Basisfunktionen. Die Liste der Basisfunktionen enthält BF7 und BF17, die Basisfunktionen, die die fehlenden Werte identifizieren. Diese Basisfunktionen sind für sich genommen nicht wichtig, da sie die nicht so stark reduziert haben wie andere Basisfunktionen in der Suche. Diese 2 Basisfunktionen sind in der Liste enthalten, um die vollständige Berechnung von BF10 und BF 19 anzuzeigen, die wichtig sind.
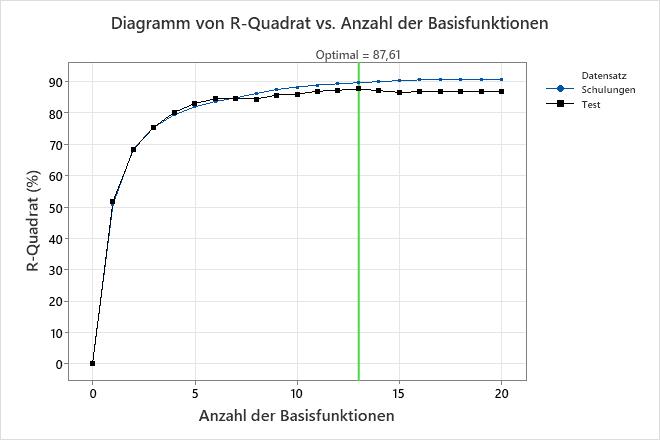
Das Diagramm R-squared vs. Anzahl der Basisfunktionen zeigt das Ergebnis der Rückwärtseliminierung, um die optimale Anzahl von Basisfunktionen zu finden. Um ein Modell mit einer anderen Anzahl von Basisfunktionen zu verwenden, wählen Sie Alternatives Modell auswählen. Wenn beispielsweise ein Modell mit viel weniger Basisfunktionen fast so genau ist wie das optimale Modell, überlegen Sie, ob Sie das einfachere Modell verwenden möchten. In diesen Ergebnissen sind die R-Squared-Werte für die Trainings- und Testdatensätze für das Modell mit 7 Basisfunktionen gleich. Dieses kleinere Modell ist von Interesse, wenn eine Überanpassung ein Problem darstellt.
Zusammenfassung des Modells
| Prädiktoren gesamt | 77 |
|---|---|
| Wichtige Prädiktoren | 10 |
| Maximale Anzahl von Basisfunktionen | 30 |
| Optimale Anzahl von Basisfunktionen | 13 |
| Statistiken | Trainings | Test |
|---|---|---|
| R-Quadrat | 89,61% | 87,61% |
| Wurzel des mittleren quadrierten Fehlers (RMSE) | 25836,5197 | 27855,6550 |
| Mittlerer quadrierter Fehler (MSE) | 667525749,7185 | 775937512,8264 |
| Mittlere abs. Abweichung (MAD) | 17506,0038 | 17783,5549 |
Die Modellübersichtstabelle enthält Messgrößen für die Leistung des Modells. Sie können diese Werte verwenden, um Modelle zu vergleichen. Für diese Ergebnisse beträgt der Test R-Quadrat etwa 88%.
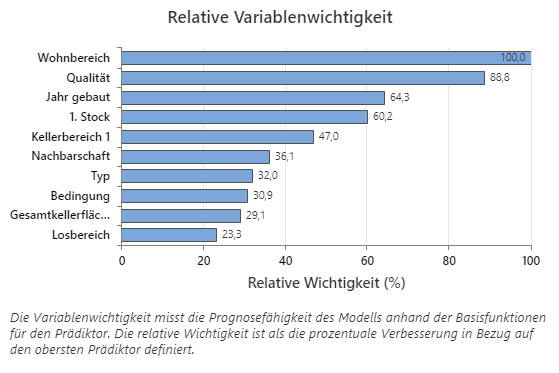
Das Diagramm zur relativen Variablenwichtigkeit stellt die Prädiktoren in der Reihenfolge ihrer Auswirkungen auf das Modell dar. Die wichtigste Prädiktorvariable ist Wohnbereich. Wenn der Beitrag der obersten Prädiktorvariablen 100% beträgt, Wohnbereich, dann hat die nächste wichtige Variable, Qualität, einen Beitrag von 88,8%. Dieser Beitrag bedeutet, dass 88,8 Qualität % so wichtig ist wie Wohnbereich in diesem Modell.
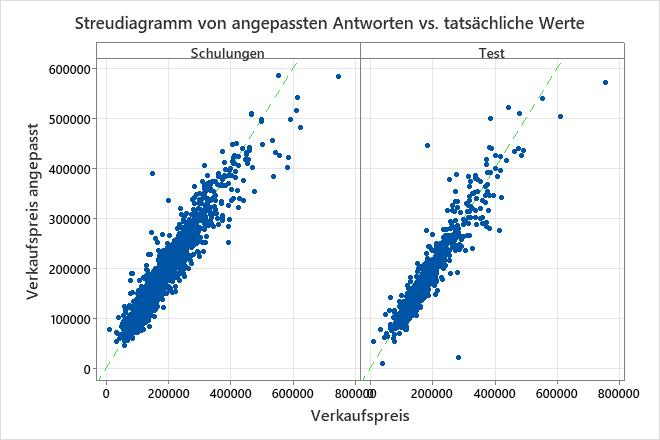
Das Streudiagramm der angepassten Verkaufspreise im Vergleich zu den tatsächlichen Verkaufspreisen zeigt die Beziehung zwischen den angepassten und den tatsächlichen Werten sowohl für die Trainingsdaten als auch für die Testdaten. Sie können mit dem Mauszeiger auf die Punkte im Diagramm zeigen, um die dargestellten Werte leichter sehen zu können. In diesem Beispiel liegen die meisten Punkte ungefähr in der Nähe der Referenzlinie von y=x.
Das Modell passt zu einigen verschiedenen Punkten schlecht, z. B. dem im Testdatensatz, der einen angepassten Verkaufspreis von weniger als 100.000 US-Dollar, aber einen tatsächlichen Verkaufspreis von 250.000 US-Dollar hat. Überlegen Sie, ob Sie diesen Fall untersuchen sollten, um die Anpassung des Modells zu verbessern.
