In diesem Thema
CART verwendet zum Berechnen von c immer den Durchschnitt von zwei benachbarten Werten. Eine stetige Variable mit N eindeutigen Werten generiert bis zu N–1 potentielle Teilungen des Elternknotens. In einer Analyse ist die tatsächliche Anzahl potenzieller Teilungen kleiner, wenn die minimale Knotengröße größer als 1 ist.
Für eine kategoriale Variable X mit den eindeutigen Werten {c1, c2, c3, ..., ck} ist eine Teilung eine Teilmenge von Stufen, die an den linken Knoten gesendet werden. Eine kategoriale Variable mit k Stufen erzeugt bis zu 2k – 1-1 Teilungen.
Für eine potenzielle Teilung während der Baumaufbauphase ist das Kriterium für Verbesserung entweder die kleinsten Quadrate (LS) oder geringste absolute Abweichung (LAD). Minitab fügt dem Baum die Teilung mit der größten Verbesserung hinzu. Wenn die Verbesserung für zwei Prädiktoren gleich ist, erfordert der Algorithmus eine Auswahl, um fortzufahren. Die Auswahl verwendet ein deterministisches Tie-Breaking-Schema, das die Position der Prädiktoren im Arbeitsblatt, den Typ des Prädiktors und die Anzahl der Klassen in einem kategorialen Prädiktor umfasst.
Minitab berechnet Verbesserungen nur anhand der Trainingsdaten, wenn die Analyse eine Methode der Modellvalidierung enthält. Verwenden Sie die folgenden Formeln, um die Verbesserung für jedes Kriterium zu berechnen.
Kleinste Quadrate (LS)

Dabei gilt Folgendes:

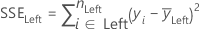

Geringste absolute Abweichung (LAD)

Dabei gilt Folgendes:

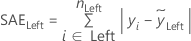

Notation
| Begriff | Beschreibung |
|---|---|
| SSE | Summe der quadrierten Fehler |
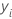 | i-ter Eintrag im Knoten |
| SAE | Summe der absoluten Fehler |
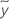 | Median der Antwort für den Knoten |
Surrogat-Teilungen
Nach dem Identifizieren einer optimalen Teilung sucht Minitab unter den anderen potenziellen Teilungen nach Surrogat-Teilungen. Eine Surrogat-Teilung ähnelt der optimalen Teilung, bei der Einträge an den linken und den rechten Knoten gesendet werden. Das Ähnlichkeitsmaß ist die Assoziation.
Eine Assoziation von 1 gibt an, dass die Surrogat-Teilung die optimale Teilung repliziert. Eine Assoziation von 0 gibt an, dass die Teilung alle Einträge an den Knoten mit mehr Datensätzen in der optimalen Teilung sendet. Teilungen mit positiver Assoziation sind potenzielle Surrogate. Verbesserungen aus Surrogat-Teilungen gehen in die Berechnungen der Variablenwichtigkeit ein.
Wenn neue Daten fehlende Werte für Prädiktoren enthalten, die Teilungen bilden, verwendet Minitab den besten nicht fehlenden Surrogat-Prädiktor anstelle des Prädiktors im Baum.
