In diesem Thema
Schritt 1: Untersuchen von Alternativbäumen
Im Diagramm von R-Quadrat vs. Anzahl der Endknoten wird das R2 für jeden Baum angezeigt. In der Standardeinstellung ist der anfängliche Regressionsbaum der kleinste Baum mit einem R2 innerhalb von 1 Standardfehler des Werts für den Baum mit dem maximalen R2. Wenn für die Analyse die Kreuzvalidierung oder ein Testdatensatz verwendet wird, stammt das R2 aus der Validierungsstichprobe. Die Werte für die Validierungsstichprobe flachen in der Regel ab und fallen schließlich mit zunehmender Größe des Baums ab.
Klicken Sie auf Alternativbaum auswählen, um ein interaktives Diagramm zu öffnen, das eine Tabelle mit Statistiken zur Zusammenfassung des Modells enthält. Verwenden Sie das Diagramm, um Alternativbäume mit ähnlicher Leistung zu untersuchen.
- Der von Minitab ausgewählte Baum ist Teil eines Musters, bei dem sich das Kriterium verbessert. Ein oder mehrere Bäume mit einigen weiteren Knoten sind Teil desselben Musters. Typischerweise möchten Sie Prognosen anhand eines Baums mit einer möglichst großen Prognosegenauigkeit treffen.
- Der von Minitab ausgewählte Baum ist Teil eines Musters, bei dem das Kriterium relativ flach ist. Eine oder mehrere Bäume mit ähnlichen Statistiken zur Zusammenfassung des Modells weisen viel weniger Knoten als der optimale Baum auf. In der Regel liefert ein Baum mit weniger Endknoten ein klareres Bild davon, wie sich die einzelnen Prädiktorvariablen auf die Werte der Antwortvariablen auswirken. Ein kleinerer Baum erleichtert auch das Identifizieren einiger Zielgruppen für weitere Untersuchungen. Wenn für einen kleineren Baum der Unterschied hinsichtlich der Prognosegenauigkeit zu vernachlässigen ist, können Sie auch die Beziehungen zwischen der Antwortvariablen und den Prädiktorvariablen anhand des kleineren Baums auswerten.
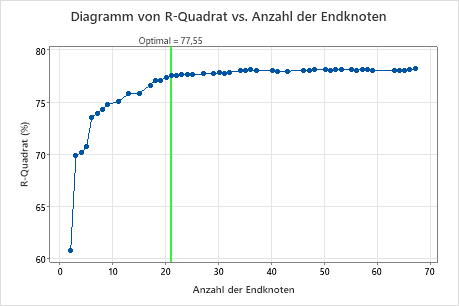
Wichtigstes Ergebnis: Diagramm von R-Quadrat vs. Anzahl der Endknoten für einen Baum mit 21 Endknoten
Der Regressionsbaum mit 21 Endknoten hat ein R2 von etwa 0,78. Dieser Baum ist mit „Optimal“ beschriftet, da das Kriterium für die Erstellung des Baums der kleinste Baum mit einem R2 innerhalb von 1 Standardabweichung des maximalen R2 war. Da dieses Diagramm zeigt, dass die R2-Werte ab Bäumen mit etwa 20 Knoten bis hin zu Bäumen mit etwa 70 Knoten relativ stabil sind, möchten die Forscher die Leistung einiger der noch kleineren Bäume betrachten, die dem Baum in den Ergebnissen ähneln. Betrachten Sie als Vergleich die nächste Grafik mit den Ergebnissen für einen Baum mit 17 Knoten.
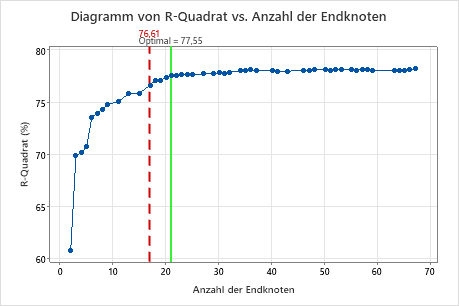
Wichtigstes Ergebnis: Diagramm von R-Quadrat vs. Anzahl der Endknoten für einen Baum mit 17 Endknoten
Der Regressionsbaum mit 17 Endknoten hat ein R2 von 0,7661. Die Beschriftung „Optimal“ für den Baum aus den anfänglichen Ergebnissen wird beibehalten, wenn Sie Alternativbaum auswählen verwenden, um Ergebnisse für einen anderen Baum zu erstellen.
Schritt 2: Untersuchen von interessanten Knoten im Baumdiagramm
Untersuchen Sie nach dem Auswählen eines Baums die eindeutigen Endknoten im Baumdiagramm. So könnten beispielsweise Knoten mit großen Mittelwerten oder kleinen Standardabweichungen von Interesse sein. In der Detailansicht sehen Sie den Mittelwert, die Standardabweichung und die Gesamtanzahlen für jeden Knoten.
Hinweis
Klicken Sie mit der rechten Maustaste auf das Baumdiagramm, um die folgenden Vorgänge auszuführen:
- Markieren Sie die fünf Knoten mit der geringsten Streuung vom angepassten Wert für den Knoten. Hierbei handelt es sich um die optimalen Knoten.
- Markieren Sie die fünf Knoten mit den höchsten Mittelwerten oder Medianen, je nach Kriterium für den Baum.
- Markieren Sie die fünf Knoten mit den niedrigsten Mittelwerten oder Medianen, je nach Kriterium für den Baum.
- Kopieren Sie die Werte der Prädiktoren, die zu einem ausgewählten Knoten führen. Diese Werte sind die Knotenregeln.
- Rufen Sie die Knotenteilungsansicht auf. Diese Ansicht ist hilfreich, wenn Sie in einem umfangreichen Baum nur die Variablen anzeigen möchten, durch welche die Knoten geteilt werden.
Knoten werden so lange weiter geteilt, bis die Endknoten nicht in weitere Gruppen geteilt werden können. Untersuchen Sie andere Knoten, um zu sehen, welche Variablen von größtem Interesse sind.
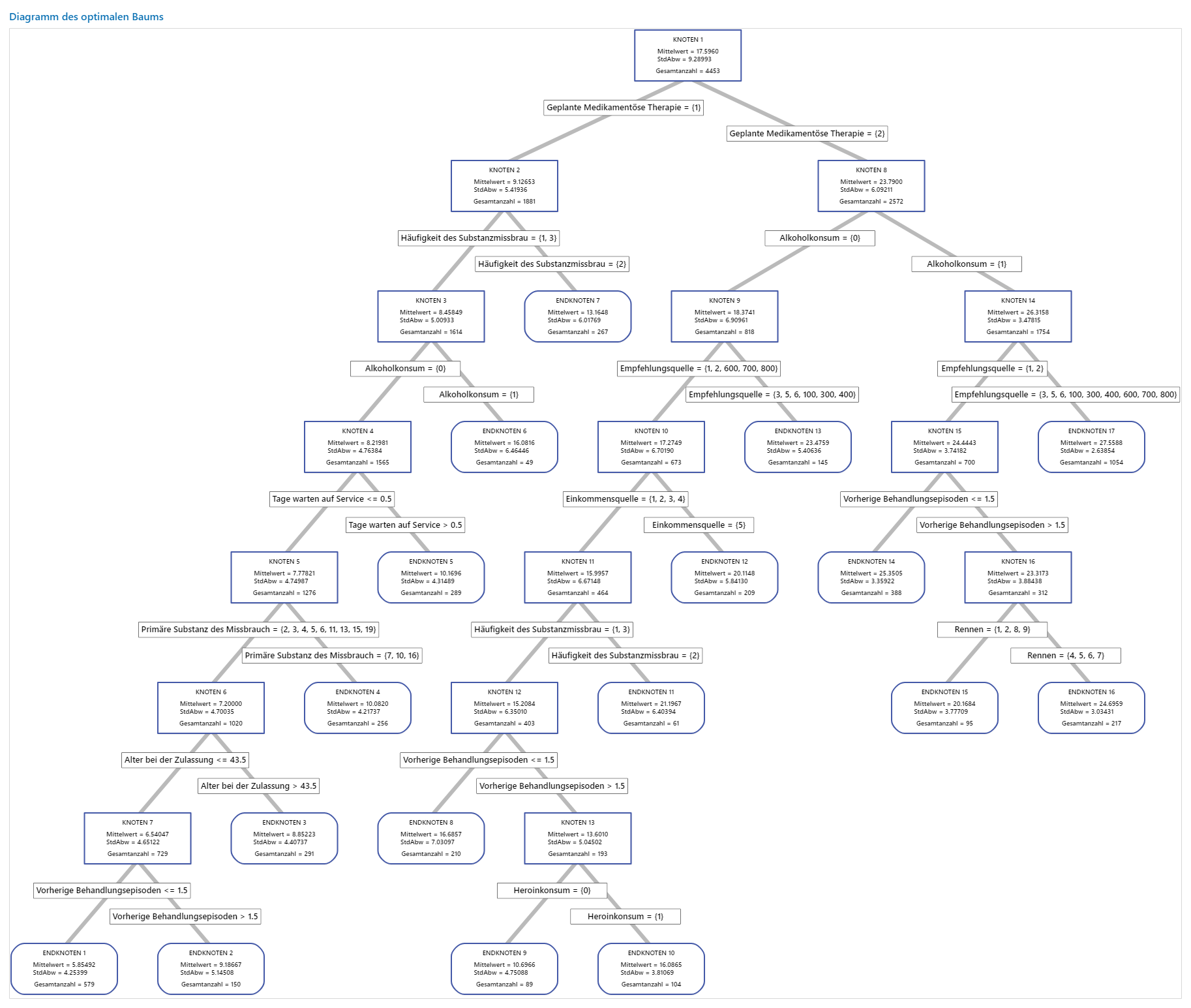
Wichtigstes Ergebnis: Baumdiagramm für einen Baum mit 17 Knoten
Das Baumdiagramm zeigt alle 4453 Fälle aus dem vollständigen Datensatz. Sie können zwischen der Detailansicht und der Knotenteilungsansicht des Baums umschalten.
- Knoten 2 enthält die Fälle, in denen Geplante Medikamentöse Therapie = 1 gilt. Dieser Knoten weist 1881 Fälle auf. Der Mittelwert für den Knoten ist kleiner als der Gesamtmittelwert. Die Standardabweichung für Knoten 2 beträgt etwa 5,4 und ist kleiner als die Gesamtstandardabweichung, da eine Teilung reinere Knoten ergibt.
- Knoten 8 enthält die Fälle, in denen Geplante Medikamentöse Therapie = 2 gilt. Dieser Knoten weist 2572 Fälle auf. Der Mittelwert für den Knoten ist größer als der Gesamtmittelwert. Die Standardabweichung für Knoten 8 beträgt etwa 6,1 und ist ebenfalls kleiner als die Gesamtstandardabweichung.
Anschließend wird Knoten 2 anhand von Häufigkeit des Substanzmissbrauchs geteilt, und Knoten 8 wird anhand von Alkoholkonsum geteilt. Endknoten 17 enthält die Fälle für Geplante Medikamentöse Therapie = 2, Alkoholkonsum = 1 und Empfehlungsquelle = 3, 5, 6, 100, 300, 400, 600, 700 oder 800. Die Forscher stellen fest, dass Endknoten 17 den höchsten Mittelwert, die kleinste Standardabweichung und die meisten Fälle aufweist.
Endknoten 1 weist den kleinsten Mittelwert auf und hat eine Standardabweichung von etwa 4,3. Da der Mittelwert von Endknoten 1 etwa 5,9 beträgt und die Werte der Antwortvariablen nicht negativ sein können, deuten die Knotenstatistiken darauf hin, dass die Daten in Endknoten 1 wahrscheinlich rechtsschief sind.
Schritt 3: Bestimmen der wichtigen Variablen
Verwenden Sie das Diagramm der relativen Variablenwichtigkeit, um zu ermitteln, welche Prädiktoren die wichtigsten Variablen für den Baum sind.
Wichtige Variablen sind primäre oder Surrogat-Teiler im Baum. Die Variable mit dem höchsten Verbesserungswert wird als wichtigste Variable festgelegt, die übrigen Variablen folgen in entsprechender Reihenfolge. Bei der relativen Variablenwichtigkeit werden die Wichtigkeitswerte standardisiert, sodass sie leichter interpretiert werden können. Die relative Wichtigkeit ist als die prozentuale Verbesserung in Bezug auf den wichtigsten Prädiktor definiert.
Die relative Variablenwichtigkeit kann Werte von 0 % bis 100 % annehmen. Die wichtigste Variable hat immer eine relative Wichtigkeit von 100 %. Befindet sich eine Variable nicht im Baum, ist sie nicht wichtig.
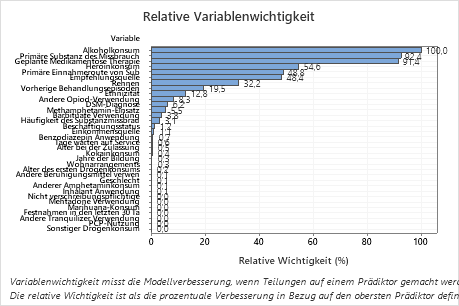
Wichtigstes Ergebnis: Relative Variablenwichtigkeit
- Primäre Substanz des Missbrauchs und Geplante Medikamentöse Therapie sind etwa 92 % so wichtig wie Alkoholkonsum.
- Heroinkonsum ist etwa 55 % so wichtig wie Alkoholkonsum.
- Primäre Einnahmeroute von Sub und Empfehlungsquelle sind etwa 48 % so wichtig wie Alkoholkonsum.
Obwohl diese Ergebnisse 33 Variablen mit positiver Wichtigkeit umfassen, liefert die relative Rangfolge Informationen darüber, wie viele Variablen für eine bestimmte Anwendung kontrolliert oder überwacht werden müssen. Ein steiler Abfall der relativen Wichtigkeit von einer Variablen zur nächsten Variablen können Ihnen die Entscheidung darüber erleichtern, welche Variablen zu kontrollieren oder zu überwachen sind. In diesen Daten weisen beispielsweise die drei wichtigsten Variablen Wichtigkeitswerte auf, die relativ nah beieinander liegen, bevor ein Abfall der relativen Wichtigkeit von fast 40 % zur nächsten Variablen zu beobachten ist. Außerdem weisen drei Variablen ähnliche Wichtigkeitswerte von annähernd 50 % auf. Sie können Variablen aus verschiedenen Gruppen entfernen und die Analyse wiederholen, um auszuwerten, wie Variablen in verschiedenen Gruppen die Prognosegenauigkeit in der Tabelle mit der Zusammenfassung des Modells beeinflussen.
