Zusammenfassung des Modells für CART^® Regression

R² ist der Prozentsatz der Streuung in der Antwortvariablen, den das Modell erklärt. Ausreißer haben eine größere Auswirkung auf das R² als auf die MAD und den MAPE.

Wenn Sie eine Validierungsmethode verwenden, enthält die Tabelle das R² für den Trainingsdatensatz und das R² für den Testdatensatz. Wenn die Validierungsmethode die Kreuzvalidierung mit K Faltungen ist, entspricht der Testdatensatz jeder Faltung, wenn diese Faltung bei der Baumerstellung ausgeschlossen wird. Das R² für den Test ist im Allgemeinen ein besseres Maß für die Eignung des Modells für neue Daten.

Interpretation

Verwenden Sie das R², um zu bestimmen, wie gut das Modell für Ihre Daten passend ist. Je höher das R², desto besser ist das Modell für Ihre Daten passend. R² liegt immer zwischen 0 % und 100 %.

Sie können die Bedeutung unterschiedlicher Werte für das R² grafisch veranschaulichen. Das erste Diagramm veranschaulicht ein einfaches Regressionsmodell, das 85,5 % der Streuung in der Antwortvariablen erklärt. Das zweite Diagramm veranschaulicht ein Modell, das 22,6 % der Streuung in der Antwortvariablen erklärt. Je mehr Streuung durch das Modell erklärt wird, desto näher liegen die Datenpunkte an den angepassten Werten. Wenn ein Modell theoretisch 100 % der Streuung erklären könnte, wären die angepassten Werte immer gleich den beobachteten Werten, und alle Datenpunkte würden auf der Linie y = x liegen.

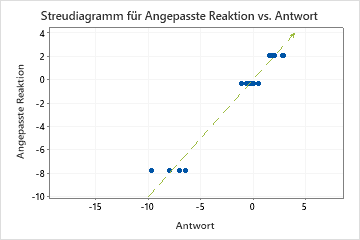
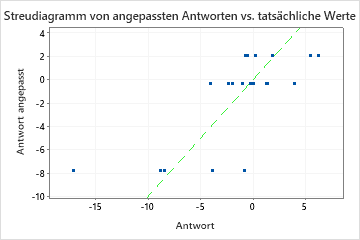
Ein R² für den Test, das erheblich kleiner als das R² für das Training ist, deutet darauf hin, dass der Baum möglicherweise besser für den aktuellen Datensatz passend ist als er die Werte der Antwortvariablen für neue Fälle prognostizieren kann.

Die Wurzel des mittleren quadrierten Fehlers (RMSE) ist ein Maß für die Genauigkeit des Baums. Ausreißer haben eine größere Auswirkung auf die RMSE als auf die MAD und den MAPE.

Wenn Sie eine Validierungsmethode verwenden, enthält die Tabelle eine RMSE für den Trainingsdatensatz und eine RMSE für den Testdatensatz. Wenn die Validierungsmethode die Kreuzvalidierung mit K Faltungen ist, entspricht der Testdatensatz jeder Faltung, wenn diese Faltung bei der Baumerstellung ausgeschlossen wird. Die RMSE für den Test ist im Allgemeinen ein besseres Maß für die Eignung des Modells für neue Daten.

Der mittlere quadrierte Fehler (MSE) ist ein Maß für die Genauigkeit des Baums. Ausreißer haben eine größere Auswirkung auf den MSE als auf die MAD und den MAPE.

Wenn Sie eine Validierungsmethode verwenden, enthält die Tabelle einen MSE für den Trainingsdatensatz und einen MSE für den Testdatensatz. Wenn die Validierungsmethode die Kreuzvalidierung mit K Faltungen ist, entspricht der Testdatensatz jeder Faltung, wenn diese Faltung bei der Baumerstellung ausgeschlossen wird. Der MSE für den Test ist im Allgemeinen ein besseres Maß für die Eignung des Modells für neue Daten.

Die mittlere absolute Abweichung (MAD) drückt die Genauigkeit in der gleichen Einheit wie die Daten aus. Auf diese Weise kann der Fehleranteil leichter erfasst werden. Ausreißer haben eine geringere Auswirkung auf die MAD als auf das R², die RMSE und den MSE.

Wenn Sie eine Validierungsmethode verwenden, enthält die Tabelle eine MAD für den Trainingsdatensatz und eine MAD für den Testdatensatz. Wenn die Validierungsmethode die Kreuzvalidierung mit K Faltungen ist, entspricht der Testdatensatz jeder Faltung, wenn diese Faltung bei der Baumerstellung ausgeschlossen wird. Die MAD für den Test ist im Allgemeinen ein besseres Maß für die Eignung des Modells für neue Daten.

Der mittlere absolute prozentuale Fehler (MAPE) drückt die Genauigkeit als Prozentsatz des Fehlers aus. Da es sich bei dem MAPE um einen Prozentsatz handelt, ist dieser Wert möglicherweise verständlicher als die anderen Genauigkeitsmaße. Wenn der MAPE beispielsweise durchschnittlich 0,05 beträgt, ist das durchschnittliche Verhältnis zwischen dem angepassten Fehler und dem tatsächlichen Wert für alle Fälle 5 %. Ausreißer haben eine geringere Auswirkung auf den MAPE als auf das R², die RMSE und den MSE.

In einigen Fällen kann jedoch ein sehr großer MAPE auftreten, obwohl der Baum gut für die Daten passend zu sein scheint. Untersuchen Sie das Diagramm der angepassten vs. tatsächlichen Werte der Antwortvariablen auf Datenwerte, die nahe 0 liegen. Da beim MAPE der absolute Fehler durch die tatsächlichen Daten dividiert wird, können Werte, die nah bei 0 liegen, den MAPE stark ansteigen lassen.

Wenn Sie eine Validierungsmethode verwenden, enthält die Tabelle einen MAPE für den Trainingsdatensatz und einen MAPE für den Testdatensatz. Wenn die Validierungsmethode die Kreuzvalidierung mit K Faltungen ist, entspricht der Testdatensatz jeder Faltung, wenn diese Faltung bei der Baumerstellung ausgeschlossen wird. Die MAPE für den Test ist im Allgemeinen ein besseres Maß für die Eignung des Modells für neue Daten.