Ein Gesundheitsdienstleister betreibt eine Einrichtung, in der Leistungen zur Behandlung von Drogenmissbrauch erbracht werden. Unter anderem bietet die Einrichtung ein ambulantes Entgiftungsprogramm mit einer regulären Behandlungsdauer von 1 bis 30 Tagen. Ein für die Planung von Personal und Ausstattung zuständiges Team möchte untersuchen, ob bessere Prognosen für die Dauer der Inanspruchnahme von Leistungen durch Patienten getroffen werden können. Grundlage hierfür sind Informationen, die bei der Aufnahme des Patienten in das Programm über den Patienten erfasst werden können. Zu diesen Variablen zählen demografische Informationen sowie Variablen über den Drogenmissbrauch des Patienten.
Zunächst zieht das Team eine traditionelle Regressionsanalyse in Minitab in Betracht. Aufgrund des fehlenden Wertemusters in ihren Daten lassen die Analyse über 70% der Daten aus. Das Auslassen eines derart großen Prozentsatzes von Daten bringt es mit sich, dass viele Informationen verloren gehen. Die Analyseergebnisse aus den Fällen ohne fehlende Daten können sich stark von den Ergebnissen unterscheiden, für die der gesamte Datensatz verwendet wird. Da die CART® Regression fehlende Werte in den Prädiktorvariablen automatisch behandelt, entscheidet das Team, die Daten mit der CART® Regression weitergehend auszuwerten.
- Öffnen Sie den Beispieldatensatz DauerDesDienstes.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antwort die Spalte 'Dauer des Dienstes' ein.
- Geben Sie im Stetige Prädiktoren 'Alter bei der Zulassung'-'Jahre der Bildung' ein.
- Geben Sie im Kategoriale Prädiktoren 'Andere stimulierende Verwendung'-'DSM-Diagnose' ein.
- Klicken Sie auf Validierung.
- Wählen Sie im Feld Validierungsmethode die Option Kreuzvalidierung mit K Faltungen aus.
- Wählen Sie Zeilen für jede Faltung nach ID-Spalte zuweisen aus.
- Geben Sie im Feld ID-Spalte die Spalte Falten ein.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
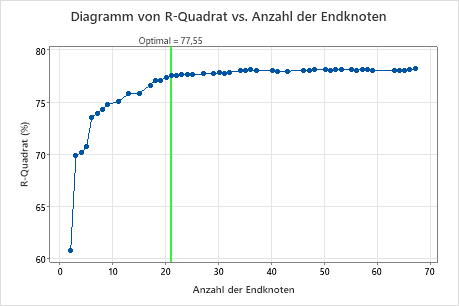
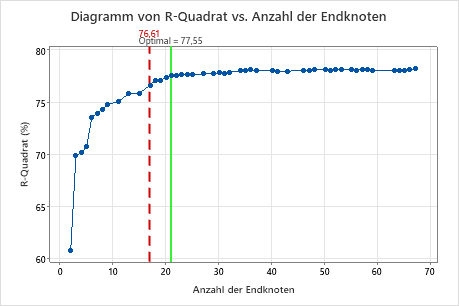
In der Standardeinstellung zeigt Minitab den kleinsten Baum mit einem R2 innerhalb von einem Standardfehler des Baums mit dem maximalen R2 an. Da das Team die Validierung mit K Faltungen verwendet, ist das Kriterium das maximale R2 für K Faltungen. Dieser Baum weist 21 Endknoten auf.
Alternativbaum auswählen
- Klicken Sie in der Ausgabe auf Alternativbaum auswählen
- Wählen Sie im Diagramm den Baum mit 17 Knoten aus.
- Klicken Sie auf Baum erstellen.
Interpretieren der Ergebnisse
Die Forscher untersuchen das Diagramm des R2 aus der Kreuzvalidierung und der Anzahl der Endknoten. Da der Baum mit 17 Knoten ein R2 aufweist, das nah an den größten Werten im Diagramm liegt, gelten die Ergebnisse für den Rest der Ausgabe für den Baum mit 17 Knoten.
Die Forscher betrachten zunächst die Zusammenfassung des Modells, um die Leistung des kleineren Baums zu bewerten. Die Werte für die Trainings- und die Teststatistiken liegen nahe beieinander, daher scheint der Baum nicht übermäßig angepasst zu sein. Das R2 ist beinahe so hoch wie die für den Baum mit 21 Knoten. Deshalb entscheiden sich die Forscher, die Beziehungen zwischen den Prädiktorvariablen und den Werte der Antwortvariablen anhand des Baums mit 17 Knoten zu untersuchen.
Methode
| Knotenteilung | Geringster quadrierter Fehler |
|---|---|
| Optimaler Baum | Innerhalb von 2,5 Standardfehlern des maximalen R-Quadrat |
| Modellvalidierung | Kreuzvalidierung mit den durch Falten definierten Zeilen |
| Verwendete Zeilen | 4453 |
Informationen zur Antwortvariablen
| Mittelwert | StdAbw | Minimum | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|
| 17,5960 | 9,29097 | 1 | 10 | 18 | 26 | 30 |
Zusammenfassung des Modells
| Prädiktoren gesamt | 44 |
|---|---|
| Wichtige Prädiktoren | 33 |
| Anzahl der Endknoten | 17 |
| Minimale Endknotengröße | 49 |
| Statistiken | Trainings | Test |
|---|---|---|
| R-Quadrat | 77,99% | 76,61% |
| Wurzel des mittleren quadrierten Fehlers (RMSE) | 4,3585 | 4,4932 |
| Mittlerer quadrierter Fehler (MSE) | 18,9967 | 20,1887 |
| Mittlere abs. Abweichung (MAD) | 3,4070 | 3,5226 |
| Mittlerer absoluter prozentualer Fehler (MAPE) | 0,6535 | 0,6674 |
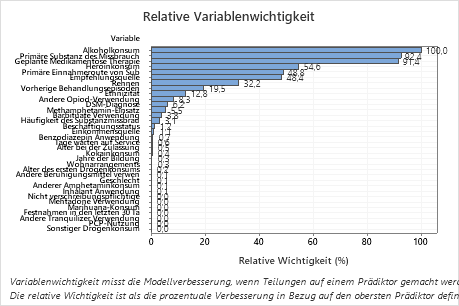
- 'Primäre Substanz des Missbrauchs' und 'Geplante Medikamentöse Therapie' sind etwa 92% so wichtig wie Alkoholkonsum.
- Heroinkonsum ist etwa 55% so wichtig wie Alkoholkonsum.
- 'Primäre Einnahmeroute von Sub' und Empfehlungsquelle sind etwa 48% so wichtig wie Alkoholkonsum.
Obwohl diese Ergebnisse 33 Variablen mit positiver Wichtigkeit umfassen, liefert die relative Rangfolge Informationen darüber, wie viele Variablen für eine bestimmte Anwendung kontrolliert oder überwacht werden müssen. Ein steiler Abfall der relativen Wichtigkeit von einer Variablen zur nächsten Variablen können Ihnen die Entscheidung darüber erleichtern, welche Variablen zu kontrollieren oder zu überwachen sind. In diesen Daten weisen beispielsweise die drei wichtigsten Variablen Wichtigkeitswerte auf, die relativ nah beieinander liegen, bevor ein Abfall der relativen Wichtigkeit von fast 40% zur nächsten Variablen zu beobachten ist. In ähnlicher Weise haben drei Variablen ähnliche Wichtigkeitswerte in der Nähe von 50%. Sie können Variablen aus verschiedenen Gruppen entfernen und die Analyse wiederholen, um auszuwerten, wie Variablen in verschiedenen Gruppen die Prognosegenauigkeit in der Tabelle mit der Zusammenfassung des Modells beeinflussen.
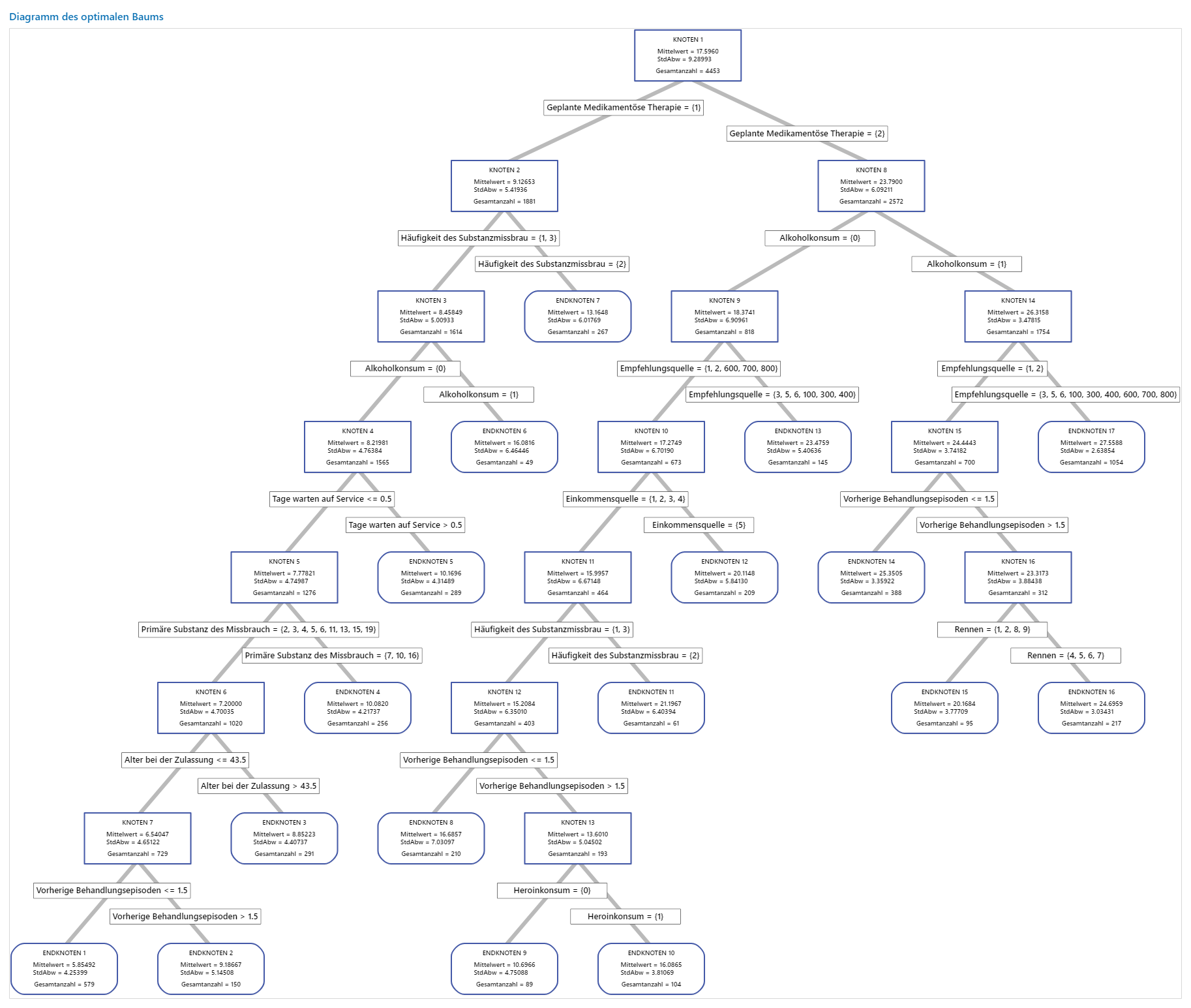
Für eine Analyse mit Kreuzvalidierung mit K Faltungen zeigt das Baumdiagramm alle 4453 Fälle aus dem vollständigen Datensatz an. Sie können zwischen der Detailansicht und der Knotenteilungsansicht des Baums umschalten. Die Tabelle der Anpassungen und Fehlerstatistiken sowie die Kriterien für die Klassifikation der Prüfobjekte liefern zusätzliche Informationen zu den Endknoten.
- Knoten 2 enthält die Fälle, für die 'Geplante Medikamentöse Therapie' = 1 gilt. Dieser Knoten weist 1881 Fälle auf. Der Mittelwert für den Knoten ist kleiner als der Gesamtmittelwert. Die Standardabweichung für Knoten 2 beträgt etwa 5,4 und ist kleiner als die Gesamtstandardabweichung, da eine Teilung reinere Knoten ergibt.
- Knoten 8 enthält die Fälle, für die 'Geplante Medikamentöse Therapie' = 2 gilt. Dieser Knoten weist 2572 Fälle auf. Der Mittelwert für den Knoten ist größer als der Gesamtmittelwert. Die Standardabweichung für Knoten 8 beträgt etwa 6,1 und ist ebenfalls kleiner als die Gesamtstandardabweichung.
Anschließend wird Knoten 2 anhand von 'Häufigkeit des Substanzmissbrauchs' geteilt, und Knoten 8 wird anhand von Alkoholkonsum geteilt. Endknoten 17 enthält die Fälle für 'Geplante Medikamentöse Therapie' = 2, Alkoholkonsum = 1 und Empfehlungsquelle = 3, 5, 6, 100, 300, 400, 600, 700 oder 800. Die Forscher stellen fest, dass Endknoten 17 den höchsten Mittelwert, die kleinste Standardabweichung und die meisten Fälle aufweist.
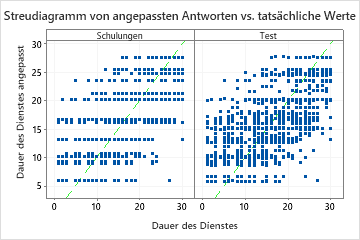
Zu den Ergebnissen zählt ein Streudiagramm der angepassten Werte der Antwortvariablen und der tatsächlichen Werte der Antwortvariablen. Die Punkte für den Trainingsdatensatz und den Testdatensatz zeigen ähnliche Muster. Diese Ähnlichkeit deutet darauf hin, dass die Leistung des Baums für neue Daten beinahe der Leistung des Baums für die Trainingsdaten entspricht.
- 'Geplante Medikamentöse Therapie' = {2}
- Alkoholkonsum = {0}
- Empfehlungsquelle = {1, 2, 600, 700, 800}
- Einkommensquelle = {1, 2, 3, 4}
- 'Häufigkeit des Substanzmissbrauchs' = {1, 3}
- 'Vorherige Behandlungsepisoden' <= 1,5
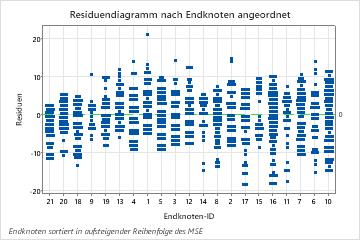
Das Diagramm der Residuen nach Endknoten zeigt, dass die Anpassung für einen kleinen Cluster von Patienten in Endknoten 8 zu stark ist. Die Analytiker erwägen zu untersuchen, weshalb einige dieser Patienten Leistungen für kürzere Zeit als ein typischer Patient in ihrer Gruppe in Anspruch nehmen. Wenn sich diese Patienten beispielsweise an einem anderen geografischen Ort als die anderen Patienten im Endknoten aufhalten, könnten unterschiedliche behördliche und versicherungsrechtliche Vorschriften beeinflussen, wie lange sie Leistungen erhalten.
Das Residuendiagramm nach Endknoten zeigt andere Fälle, bei denen Analytiker sich für die Untersuchung von Clustern oder Ausreißern entscheiden könnten. In diesen Daten liegt z. B. ein Residuum vor, das viel größer als die anderen in Endknoten 1 und Endknoten 7 erscheint. Die Analytiker entscheiden sich, den Grund zu untersuchen, aus dem die betreffenden Patienten Leistungen länger als andere Patienten in ihrem Endknoten in Anspruch nahmen.
Da das R2 verbessert werden kann und die Residuendiagramme Fälle aufzeigen, für die der Baum nicht gut passend ist, überlegen die Forscher, ob sie versuchen sollten, die Anpassung des Baumes mit einer TreeNet® Regression oder einer Random Forests® Regression zu verbessern.