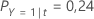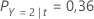Ein Klassifikationsbaum ergibt sich aus einer binären rekursiven Partitionierung des ursprünglichen Trainingsdatensatzes. Jeder Elternknoten (eine Teilmenge von Trainingsdaten) in einem Baum kann in einer endlichen Anzahl von Möglichkeiten in zwei einander ausschließende Kindknoten geteilt werden; die Möglichkeiten hängen von den tatsächlichen Datenwerten ab, die im Knoten erfasst sind.
Das Teilungsverfahren behandelt Prädiktorvariablen als stetig oder kategorial. Für eine stetige Variable X und einen Wert c wird eine Teilung definiert, indem alle Datensätze mit den Werten X, die kleiner oder gleich c sind, an den linken Knoten und alle verbleibenden Datensätze an den rechten Knoten gesendet werden. CART verwendet zum Berechnen von c immer den Durchschnitt von zwei benachbarten Werten. Eine stetige Variable mit N unterschiedlichen Werten generiert bis zu N–1 potenzielle Teilungen des Elternknotens (die tatsächliche Anzahl ist kleiner, wenn Grenzwerte für die minimal zulässige Knotengröße festgelegt werden).
Ein stetiger Prädiktor verfügt z. B. in den Daten über die Werte 55, 66 und 75. Eine mögliche Teilung für diese Variable besteht darin, dass alle Werte, die kleiner oder gleich (55+66)/2 = 60,5 sind, an einen Kindknoten und alle Werte, die größer als 60,5 sind, an den anderen Kindknoten zu senden. Fälle mit dem Prädiktorwert 55 gehen an einen Knoten, während die Fälle mit den Werten 66 und 75 an den anderen Knoten gesendet werden. Die andere mögliche Teilung für diesen Prädiktor besteht darin, dass alle Werte, die kleiner oder gleich 70,5 sind, an einen Kindknoten und Werte, die größer als 70,5 sind, an den anderen Knoten gesendet werden. Fälle mit den Werten 55 und 66 werden an einen Knoten gesendet, während Fälle mit dem Wert 75 an den anderen Knoten gesendet werden.
Für eine kategoriale Variable X mit unterschiedlichen Werten {c1, c2, …, ck} wird eine Teilung als Teilmenge von Stufen definiert, die an den linken Kindknoten gesendet werden. Eine kategoriale Variable mit K Stufen generiert bis zu 2K-1–1 Teilungen.
| Linker Kindknoten | Rechter Kindknoten |
|---|---|
| Rot, Blau | Gelb |
| Rot, Gelb | Blau |
| Blau, Gelb | Rot |
Bei Klassifikationsbäumen ist das Ziel multinomial, mit K eindeutigen Klassen. Das Hauptziel des Baums besteht darin, eine Möglichkeit zu finden, unterschiedliche Zielklassen so rein wie möglich in einzelne Knoten zu trennen. Die resultierende Anzahl von Endknoten muss nicht K sein. Es können mehrere Endknoten verwendet werden, um eine bestimmte Zielklasse darzustellen. Ein Benutzer kann frühere Wahrscheinlichkeiten für die Zielklassen angeben. Diese werden von CART während des Wachstums des Baums berücksichtigt.
In den folgenden Abschnitten verwendet Minitab die folgenden Definitionen für eine binäre Antwortvariable:
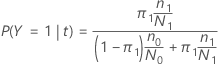
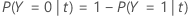
In den folgenden Abschnitten verwendet Minitab die folgenden Definitionen für eine multinomiale Antwortvariable:
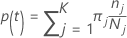
Die Wahrscheinlichkeit von Klasse j bei gegebenem Knoten t:
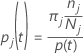
Diese Definitionen geben die Wahrscheinlichkeiten innerhalb des Knotens an. Minitab berechnet diese Wahrscheinlichkeiten für jeden Knoten und jede mögliche Teilung. Minitab berechnet die Gesamtverbesserung für eine mögliche Teilung aus diesen Wahrscheinlichkeiten anhand eines der folgenden Kriterien.
Notation
| Begriff | Beschreibung |
|---|---|
| K | Anzahl der Klassen in der Antwortvariablen |
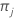 | A-priori-Wahrscheinlichkeit für Klasse j |
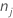 | Anzahl der Beobachtungen für Klasse j in einem Knoten |
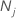 | Anzahl der Beobachtungen für Klasse j in den Daten |
Gini-Kriterium
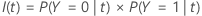
Die folgende allgemeinere Formel gilt für eine multinomiale Antwortvariable:
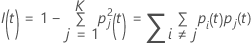
Befinden sich alle Beobachtungen für einen Knoten in einer Klasse, ist
Folgendes zu beachten:  .
.
Entropiekriterium

Die folgende allgemeinere Formel gilt für eine multinomiale Antwortvariable:
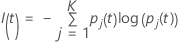
Befinden sich alle Beobachtungen für einen Knoten in einer Klasse, ist
Folgendes zu beachten:  .
.
Twoing-Kriterium
| Superklasse 1 | Superklasse 2 |
|---|---|
| 1, 2, 3 | 4 |
| 1, 2, 3 | 3 |
| 1, 3, 4 | 2 |
| 2, 3, 4 | 1 |
| 1, 2 | 3, 4 |
| 1, 3 | 2, 4 |
| 1, 4 | 2, 3 |


Die linke Superklasse enthält alle Zielklassen, die sich tendenziell links befinden. Die rechte Superklasse enthält alle Zielklassen, die sich tendenziell rechts befinden.
| Klasse | Wahrscheinlichkeit des linken Kindknotens | Wahrscheinlichkeit des rechten Kindknotens |
|---|---|---|
| 1 | 0,67 | 0,33 |
| 2 | 0,82 | 0,18 |
| 3 | 0,23 | 0,77 |
| 4 | 0,89 | 0,11 |
Die beste Möglichkeit, die Superklassen für die potenzielle Teilung zu erstellen, besteht darin, {1, 2, 4} als eine Superklasse und {3} als die andere Superklasse zuzuweisen.
Der Rest der Berechnung entspricht der für das Gini-Kriterium mit den Superklassen als binäres Ziel.
Verbesserungsberechnung für die Kriterien
Nachdem Minitab die Unreinheit der Knoten berechnet hat, werden die bedingten Wahrscheinlichkeiten für das Teilen des Knotens mit einem Prädiktor berechnet:

und

Dann stammt die Verbesserung für eine Teilung aus der folgenden Formel:

Der Split mit dem höchsten Verbesserungswert wird Teil des Baumes. Wenn die Verbesserung für zwei Prädiktoren gleich ist, erfordert der Algorithmus eine Auswahl, um fortzufahren. Die Auswahl verwendet ein deterministisches Tie-Breaking-Schema, das die Position der Prädiktoren im Arbeitsblatt, den Typ des Prädiktors und die Anzahl der Klassen in einem kategorialen Prädiktor umfasst.
Klassenwahrscheinlichkeit
Knotenteilungen maximieren die Wahrscheinlichkeit einer Klasse innerhalb eines bestimmten Knotens.
Endknoten
- Die Anzahl der Fälle im Knoten erreicht die minimale Größe für die Analyse. Das Standardminimum in der Minitab Statistical Software beträgt 3.
- Alle Fälle in einem Knoten weisen dieselbe Klasse der Antwortvariablen auf.
- Alle Fälle in einem Knoten verfügen über die gleichen Prädiktorwerte.
Prognostizierte Klasse für einen Endknoten
Die prognostizierte Klasse für einen Endknoten ist die Klasse, welche die Fehlklassifikationskosten für den Knoten minimiert. Darstellungen der Fehlklassifikationskosten hängen von der Anzahl der Klassen in der Antwortvariablen ab. Da die prognostizierte Klasse für einen Endknoten bei Nutzung einer Validierungsmethode aus den Trainingsdaten stammt, verwenden alle folgenden Formeln Wahrscheinlichkeiten aus dem Trainingsdatensatz.
Binäre Antwortvariable
Die folgende Gleichung gibt die Fehlklassifikationskosten für die Prognose an, dass die Fälle im Knoten die Ereignisklasse darstellen:

Die folgende Gleichung gibt die Fehlklassifikationskosten für die Prognose an, dass die Fälle im Knoten die Nicht-Ereignisklasse darstellen:

| Begriff | Beschreibung |
|---|---|
| PY=0|t | bedingte Wahrscheinlichkeit, dass ein Fall im Knoten t zur Nicht-Ereignisklasse gehört |
| C1|0 | Fehlklassifikationskosten, dass ein Fall der Nicht-Ereignisklasse als Fall der Ereignisklasse prognostiziert wird |
| PY=1|t | bedingte Wahrscheinlichkeit, dass ein Fall im Knoten t zur Ereignisklasse gehört |
| C0|1 | Fehlklassifikationskosten, dass ein Fall der Ereignisklasse als Fall der Nicht-Ereignisklasse prognostiziert wird |
Die prognostizierte Klasse für einen Endknoten ist die Klasse mit den minimalen Fehlklassifikationskosten.
Multinomiale Antwortvariable

Betrachten Sie beispielsweise eine Antwortvariable mit drei Klassen und den folgenden Fehlklassifikationskosten:
| Prognostizierte Klasse | |||
| Tatsächliche Klasse | 1 | 2 | 3 |
| 1 | 0,0 | 4,1 | 3,2 |
| 2 | 5,6 | 0,0 | 1,1 |
| 3 | 0,4 | 0,9 | 0,0 |
Bedenken Sie dann, dass die Klassen der Antwortvariablen die folgenden Wahrscheinlichkeiten für diesen Knoten haben: t:
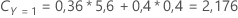


Die niedrigsten Fehlklassifikationskosten gelten für die Prognose, dass Y = 3; 1,164. Diese Klasse ist die prognostizierte Klasse für den Endknoten.