Wichtige Prädiktoren
Jeder Klassifikationsbaum ist eine Auflistung von Teilungen. Jede Teilung trägt zur Verbesserung des Baums bei. Jede Teilung enthält außerdem Surrogat-Teilungen, die ebenfalls eine Verbesserungen des Baums bewirken. Die Wichtigkeit einer Variablen wird durch alle ihre Verbesserungen angegeben, wenn der Baum die Variable zum Teilen eines Knotens oder bei Vorliegen eines fehlenden Werts in einer anderen Variablen als Surrogat zum Teilen eines Knotens verwendet.
Mit der folgenden Formel wird die Verbesserung an einem einzelnen Knoten berechnet:
Die Werte von I(t), pLinks und pRechts hängen vom Kriterium zum Teilen der Knoten ab. Weitere Informationen finden Sie unter Knotenteilungsmethoden in CART® Klassifikation.
Durchschnittliche –Log-Likelihood
Trainingsdaten oder keine Validierung
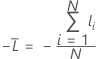
Dabei gilt Folgendes:
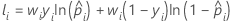
Notation für Trainingsdaten oder keine Validierung
| Begriff | Beschreibung |
|---|---|
| N | Stichprobenumfang der vollständigen Daten oder der Trainingsdaten |
| wi | Gewichtung für die i-te Beobachtung im ganzen Datensatz oder im Trainingsdatensatz |
| yi | Indikatorvariable, die für den vollständigen oder Trainingsdatensatz 1 für das Ereignis und andernfalls 0 ist |
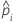 | prognostizierte Wahrscheinlichkeit des Ereignisses für die i-te Zeile im vollständigen oder Trainingsdatensatz |
Kreuzvalidierung mit K Faltungen
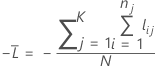
Dabei gilt Folgendes:
Notation für Kreuzvalidierung mit K Faltungen
| Begriff | Beschreibung |
|---|---|
| N | Stichprobenumfang der vollständigen Daten oder Trainingsdaten |
| nj | Stichprobenumfang der Faltung j |
| wij | Gewichtung für die i-te Beobachtung in Faltung j |
| yij | Indikatorvariable, die 1 ist für das Ereignis, andernfalls 0 für die Daten in Faltung j |
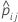 | prognostizierte Wahrscheinlichkeit des Ereignisses aus der Modellschätzung, die nicht die Beobachtungen für die i-te Beobachtung in Faltung j einschließt |
Testdatensatz
Dabei gilt Folgendes:
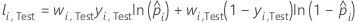
Notation für Testdatensatz
| Begriff | Beschreibung |
|---|---|
| nTest | Stichprobenumfang des Testdatensatzes |
| wi, Test | Gewichtung für die i-te Beobachtung im Testdatensatz |
| yi, Test | Indikatorvariable, die 1 ist für das Ereignis, andernfalls 0 für Daten im Testdatensatz |
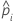 | prognostizierte Wahrscheinlichkeit des Ereignisses für die i-te Zeile im Testdatensatz |
Fläche unterhalb der ROC-Kurve
Formel
Für die Fläche unterhalb der Kurve verwendet Minitab eine Integration.
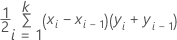
Hierbei ist k die Anzahl der Endknoten und (x0, y0) ist der Punkt (0, 0).
| x (Falsch-Positiv-Rate) | y (Richtig-Positiv-Rate) |
|---|---|
| 0,0923 | 0,3051 |
| 0,4154 | 0,7288 |
| 0,7538 | 0,9322 |
| 1 | 1 |
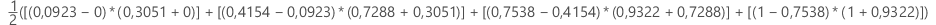
Notation
| Begriff | Beschreibung |
|---|---|
| TRP | Richtig-Positiv-Rate |
| FPR | Falsch-Positiv-Rate |
| TP | Richtig positiv; Ereignisse, die richtig bewertet wurden |
| P | Anzahl der tatsächlichen positiven Ereignisse |
| FP | Richtig negativ; Nicht-Ereignisse, die richtig bewertet wurden |
| N | Anzahl der tatsächlichen negativen Ereignisse |
| FNR | Falsch-Negativ-Rate |
| TNR | Richtig-Negativ-Rate |
95%-KI für die Fläche unterhalb der ROC-Kurve
Das folgende Intervall gibt die Ober- und die Untergrenze für das Konfidenzintervall an:
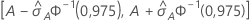
Die Berechnung des Standardfehlers der Fläche unterhalb der ROC-Kurve (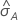
) stammt aus dem Salford Predictive Modeler®. Allgemeine Informationen zum Schätzen der Varianz der Fläche unterhalb ROC-Kurve finden Sie in den folgenden Veröffentlichungen:
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations. In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer. doi:10.1007/978-3-642-16114-8
Cortes, C. and Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305–312.
Feng, D., Cortese, G., und Baumgartner, R. (2017). A comparison of confidence/credible interval methods for the area under the ROC curve for continuous diagnostic tests with small sample size. Statistical Methods in Medical Research, 26(6), 2603–2621. doi:10.1177/0962280215602040
Notation
| Begriff | Beschreibung |
|---|---|
| A | Fläche unterhalb der ROC-Kurve |
 | 0,975 Perzentil der Standardnormalverteilung |
Lift
Formel
Verwenden Sie für die 10 % der Beobachtungen in den Daten mit der höchsten Wahrscheinlichkeit der Zuweisung zur Ereignisklasse die folgende Formel.
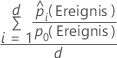
Verwenden Sie für den Test-Lift mit einem Testdatensatz Beobachtungen aus dem Testdatensatz. Wählen Sie für den Test-Lift mit Kreuzvalidierung mit K Faltungen die zu verwendenden Daten aus, und berechnen Sie den Lift anhand der prognostizierten Wahrscheinlichkeiten für Daten, die nicht in der Modellschätzung enthalten sind.
Notation
| Begriff | Beschreibung |
|---|---|
| d | Anzahl der Fälle in 10 % der Daten |
 | prognostizierte Wahrscheinlichkeit des Ereignisses |
 | Wahrscheinlichkeit des Ereignisses in den Trainingsdaten oder, wenn für die Analyse keine Validierung verwendet wird, im vollständigen Datensatz |
Fehlklassifikationskosten
Die Fehlklassifikationskosten in der Tabelle mit der Zusammenfassung des Modells sind die relativen Fehlklassifikationskosten für das Modell relativ zu einem trivialen Klassifikator, der alle Beobachtungen in die häufigste Klasse klassifiziert.
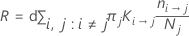
Die relativen Fehlklassifikationskosten haben folgende Form:
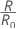
Hierbei sind R0 die Kosten für den trivialen Klassifikator.
Die Formel für R wird vereinfacht, wenn die A-priori-Wahrscheinlichkeiten gleich sind oder aus den Daten stammen.
Gleiche A-priori-Wahrscheinlichkeiten
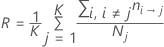
A-priori-Wahrscheinlichkeiten aus den Daten
Mit dieser Definition weist R die folgende Form auf:
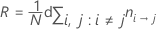
Notation
| Begriff | Beschreibung |
|---|---|
| πj | A-priori-Wahrscheinlichkeit der j. Klasse der Antwortvariablen |
 | Kosten für die Fehlklassifizierung der Klasse i als Klasse j |
 | Anzahl der Klassen-I-Datensätze, die fälschlicherweise als Klasse j klassifiziert wurden |
| Nj | Anzahl der Fälle in der j. Klasse der Antwortvariablen |
| K | Anzahl der Klassen in der Antwortvariablen |
| N | Anzahl der Fälle in den Daten |
