In diesem Thema
Schritt 1: Untersuchen von Alternativbäumen
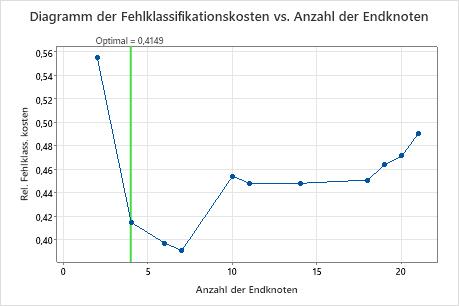
Das Diagramm der Fehlklassifikationskosten vs. Anzahl der Endknoten zeigt die Fehlklassifikationskosten für jeden Baum in der Sequenz an, die den optimale Baum erzeugt. In der Standardeinstellung ist der anfängliche optimale Baum der kleinste Baum mit Fehlklassifikationskosten innerhalb von einem Standardfehler des Baums, der die Fehlklassifikationskosten minimiert. Wenn für die Analyse die Kreuzvalidierung oder ein Testdatensatz verwendet wird, stammen die Fehlklassifikationskosten aus der Validierungsstichprobe. Die Fehlklassifikationskosten für die Validierungsstichprobe nehmen in der Regel ab und steigen schließlich mit zunehmender Größe des Baums.
- Der optimale Baum ist Teil eines Musters, bei dem die Fehlklassifikationskosten abnehmen. Ein oder mehrere Bäume mit einigen weiteren Knoten sind Teil desselben Musters. Typischerweise möchten Sie Prognosen anhand eines Baums mit einer möglichst großen Prognosegenauigkeit treffen. Wenn der Baum einfach genug ist, können Sie anhand des Baums auch ein Verständnis der Auswirkung der einzelnen Prädiktorvariablen auf die Werte der Antwortvariablen erlangen.
- Der optimale Baum ist Teil eines Musters, bei dem die Linie der Fehlklassifikationskosten relativ flach ist. Eine oder mehrere Bäume mit ähnlichen Statistiken zur Zusammenfassung des Modells weisen viel weniger Knoten als der optimale Baum auf. In der Regel liefert ein Baum mit weniger Endknoten ein klareres Bild davon, wie sich die einzelnen Prädiktorvariablen auf die Werte der Antwortvariablen auswirken. Ein kleinerer Baum erleichtert auch das Identifizieren einiger Zielgruppen für weitere Untersuchungen. Wenn für einen kleineren Baum der Unterschied hinsichtlich der Prognosegenauigkeit zu vernachlässigen ist, können Sie auch die Beziehungen zwischen der Antwortvariablen und den Prädiktorvariablen anhand des kleineren Baums auswerten.
Zusammenfassung des Modells
| Prädiktoren gesamt | 13 |
|---|---|
| Wichtige Prädiktoren | 13 |
| Anzahl der Endknoten | 4 |
| Minimale Endknotengröße | 27 |
| Statistiken | Trainings | Test |
|---|---|---|
| Durchschnittliche -Log-Likelihood | 0,4772 | 0,5164 |
| Fläche unter der ROC-Kurve | 0,8192 | 0,8001 |
| 95%-KI | (0,3438; 1) | (0,7482; 0,8520) |
| Lift | 1,6189 | 1,8849 |
| Fehlklassifikationskosten | 0,3856 | 0,4149 |
Wichtigste Ergebnisse: Diagramm und Zusammenfassung des Modells für einen Baum mit vier Knoten
Der Baum in der Sequenz mit vier Knoten weist Fehlklassifikationskosten von etwa 0,41 auf. Das Muster mit abnehmenden Fehlklassifikationskosten setzt sich nach dem Baum mit vier Knoten fort. In einem solchen Fall entscheiden sich die Analytiker dafür, einige der anderen einfachen Bäume zu untersuchen, die niedrigere Fehlklassifikationskosten aufweisen.
Zusammenfassung des Modells
| Prädiktoren gesamt | 13 |
|---|---|
| Wichtige Prädiktoren | 13 |
| Anzahl der Endknoten | 7 |
| Minimale Endknotengröße | 5 |
| Statistiken | Trainings | Test |
|---|---|---|
| Durchschnittliche -Log-Likelihood | 0,3971 | 0,5094 |
| Fläche unter der ROC-Kurve | 0,8861 | 0,8200 |
| 95%-KI | (0,5590; 1) | (0,7702; 0,8697) |
| Lift | 1,9376 | 1,8165 |
| Fehlklassifikationskosten | 0,2924 | 0,3909 |
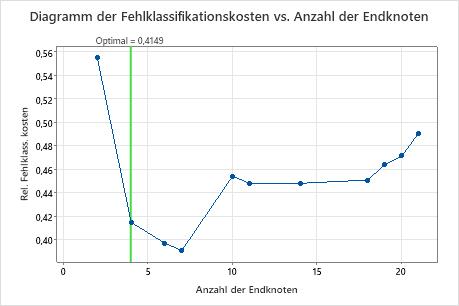
Wichtigste Ergebnisse: Diagramm und Zusammenfassung des Modells für einen Baum mit sieben Knoten
Der Klassifikationsbaum, der die relativen kreuzvalidierten Fehlklassifikationskosten minimiert, weist sieben Endknoten und relative Fehlklassifikationskosten von etwa 0,39 auf. Andere Statistiken wie die Fläche unter der ROC-Kurve bestätigen ebenfalls, dass der Baum mit sieben Knoten eine bessere Leistung als der Baum mit vier Knoten bietet. Da der Baum mit sieben Knoten eine so kleine Anzahl von Knoten hat, dass er leicht zu interpretieren ist, entscheiden sich die Analytiker, anhand des Baums mit sieben Knoten die wichtigen Variablen zu untersuchen und Prognosen vorzunehmen.
Schritt 2: Untersuchen der reinsten Endknoten im Baumdiagramm
Untersuchen Sie nach dem Auswählen eines Baums die reinsten Endknoten im Diagramm. Die Ereignisstufe wird durch die Farbe Blau dargestellt, während die Nicht-Ereignisstufe durch die Farbe Rot dargestellt wird.
Hinweis
Sie können mit der rechten Maustaste auf das Baumdiagramm klicken, um die Knotenteilungsansicht des Baums anzuzeigen. Diese Ansicht ist hilfreich, wenn Sie in einem umfangreichen Baum nur die Variablen anzeigen möchten, durch welche die Knoten geteilt werden.
Knoten werden so lange weiter geteilt, bis die Endknoten nicht in weitere Gruppen geteilt werden können. Die Knoten, die überwiegend blau sind, weisen auf einen starken Anteil der Ereignisstufe hin. Die Knoten, die überwiegend rot sind, weisen auf einen starken Anteil der Nicht-Ereignisstufe hin.
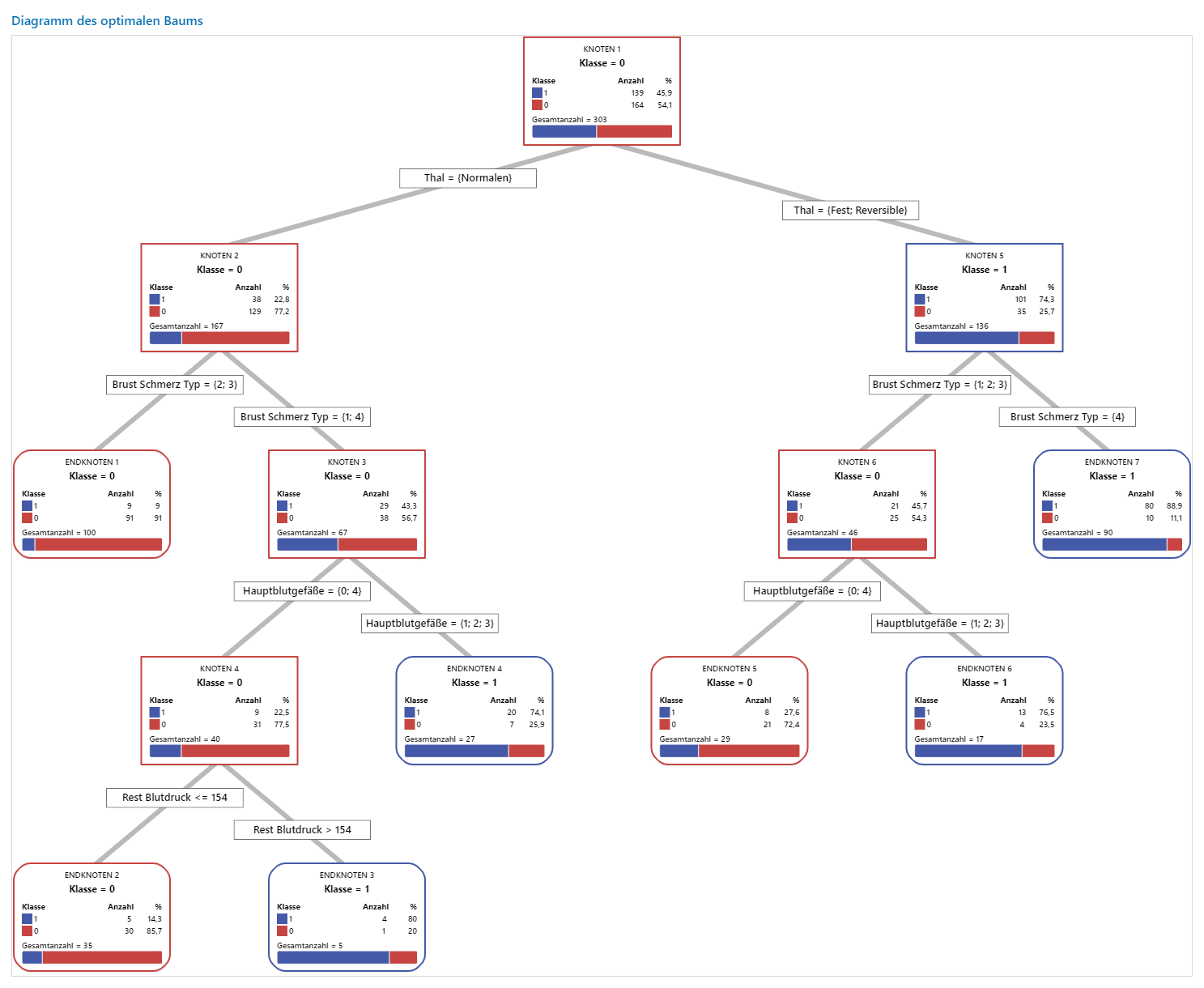
Wichtigstes Ergebnis: Baumdiagramm
Dieser Klassifikationsbaum weist sieben Endknoten auf. Blau steht für die Ereignisstufe (Ja) und Rot für die Nicht-Ereignisstufe (Nein). Im Baumdiagramm wird der Trainingsdatensatz verwendet. Sie können zwischen der Detailansicht und der Knotenteilungsansicht des Baums umschalten.
- Knoten 2: THAL war für 167 Fälle Normal. Von den 167 Fällen sind 38 bzw. 22,8 % gleich Ja und 129 bzw. 77,2 % gleich Nein.
- Knoten 5: THAL war für 136 Fälle Fest oder Reversibel. Von den 136 Fällen sind 101 bzw. 74,3% gleich Ja und 35 bzw. 25,7% gleich Nein.
Der nächste Teiler für den linken Kindknoten und den rechten Kindknoten ist „Brustschmerztyp“, wobei der Schmerz als1, 2, 3 oder 4 eingestuft wird. Knoten 2 ist der Elternknoten von Endknoten 1, und Knoten 5 ist der Elternknoten von Endknoten 7.
- Endknoten 1: Für 100 Fälle war THAL Normal, und „Brustschmerz“ war 2 oder 3. Von den 100 Fällen sind 9 bzw. 9% gleich Ja und 91 bzw. 91% gleich Nein.
- Endknoten 7: Für 90 Fälle war THAL Fest oder Reversible, und „Brustschmerz“ betrug 4. Von den 90 Fällen sind 80 bzw. 88,9% gleich Ja und 10 bzw. 11,1% gleich Nein.
Schritt 3: Bestimmen der wichtigen Variablen
Verwenden Sie das Diagramm der relativen Variablenwichtigkeit, um zu ermitteln, welche Prädiktoren die wichtigsten Variablen für den Baum sind.
Wichtige Variablen sind primäre oder Surrogat-Teiler im Baum. Die Variable mit dem höchsten Verbesserungswert wird als wichtigste Variable festgelegt, die übrigen Variablen folgen in entsprechender Reihenfolge. Bei der relativen Variablenwichtigkeit werden die Wichtigkeitswerte standardisiert, sodass sie leichter interpretiert werden können. Die relative Wichtigkeit ist als die prozentuale Verbesserung in Bezug auf den wichtigsten Prädiktor definiert.
Die Werte für die relative variable Wichtigkeit reichen von 0 % bis 100 %. Die wichtigste Variable hat immer eine relative Bedeutung von 100%. Befindet sich eine Variable nicht im Baum, ist sie nicht wichtig.
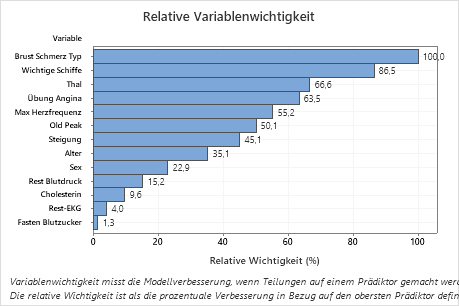
Wichtigstes Ergebnis: Relative Variablenwichtigkeit
- Hauptblutgefäße ist etwa 87% so wichtig wie Brust Schmerz Typ.
- Thal und Übung Angina sind beide etwa 65% so wichtig wie Brust Schmerz Typ.
- Max Herzfrequenz ist etwa 55% so wichtig wie Brust Schmerz Typ.
- Old Peak ist etwa 50% so wichtig wie Brust Schmerz Typ.
- Steigung, Alter, und Sex Rest Blutdruck sind viel weniger wichtig als Brust Schmerz Typ.
Obwohl sie eine positive Bedeutung haben, könnten Analysten entscheiden, dass Cholesterin, Rest-EKGund Fasten Blutzucker keine wichtigen Beiträge zur Struktur leisten.
Schritt 4: Bewerten der Prognosefähigkeit des Baums
Der genaueste Baum ist der Baum mit den niedrigsten Fehlklassifikationskosten. Manchmal funktionieren einfachere Bäume mit etwas höheren Fehlklassifikationskosten genauso gut. Sie können das Diagramm Fehlklassifikation vs. Endknoten verwenden, um alternative Bäume zu identifizieren.
Die Grenzwertoptimierungskurve (ROC-Kurve) veranschaulicht, wie gut ein Baum die Daten klassifiziert. Die ROC-Kurve bildet die Richtig-Positiv-Rate auf der y-Achse und die Falsch-Positiv-Rate auf der x-Achse ab. Die Richtig-Positiv-Rate wird auch als Trennschärfe bezeichnet. Die Falsch-Positiv-Rate wird auch als Fehler 1. Art bezeichnet.
Wenn ein Klassifikationsbaum Kategorien in der Antwortvariablen perfekt trennen kann, ist die Fläche unter der ROC-Kurve 1; dies entspricht dem bestmöglichen Klassifikationsmodell. Wenn eine Klassifikationsbaum Kategorien nicht unterscheiden kann und Zuordnungen komplett zufällig vornimmt, beträgt die Fläche unter der ROC-Kurve 0,5.
Wenn Sie den Baum mit einem Validierungsverfahren erstellen, stellt Minitab Informationen zur Leistung des Baums in den Trainings- und Validierungsdaten (Testdaten) bereit. Wenn die Kurven nah beieinander liegen, können Sie mit größerer Sicherheit behaupten, dass der Baum keine übermäßige Anpassung aufweist. Die Leistung des Baums mit den Testdaten gibt an, wie gut der Baum neue Daten prognostizieren kann.
- Richtig-Positiv-Rate (TPR): Die Wahrscheinlichkeit, dass ein Ereignisfall richtig prognostiziert wird.
- Falsch-Positiv-Rate (FPR): Die Wahrscheinlichkeit, dass ein Nicht-Ereignisfall falsch prognostiziert wird.
- Falsch-Negativ-Rate (FNR): Die Wahrscheinlichkeit, dass ein Ereignisfall falsch prognostiziert wird.
- Richtig-Negativ-Rate (TNR): Die Wahrscheinlichkeit, dass ein Nicht-Ereignisfall richtig prognostiziert wird.
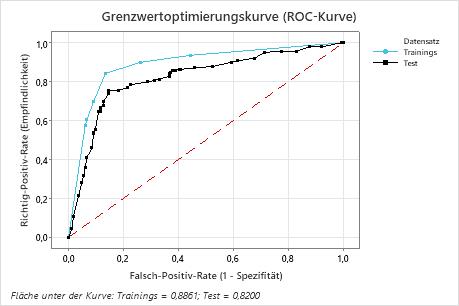
Wichtigstes Ergebnis: Grenzwertoptimierungskurve (ROC-Kurve)
In diesem Beispiel beträgt die Fläche unter der ROC-Kurve für Training 0,886 und für Tests 0,82. Diese Werte weisen darauf hin, dass der Klassifikationsbaum in den meisten Anwendungen ein sinnvoller Klassifikator ist.
Konfusionsmatrix
| Prognostizierte Klasse (Trainings) | Prognostizierte Klasse (Test) | ||||||
|---|---|---|---|---|---|---|---|
| Tatsächliche Klasse | |||||||
| Anzahl | 1 | 0 | % Richtig | 1 | 0 | % Richtig | |
| 1 (Ereignis) | 139 | 117 | 22 | 84,2 | 105 | 34 | 75,5 |
| 0 | 164 | 22 | 142 | 86,6 | 24 | 140 | 85,4 |
| Alle | 303 | 139 | 164 | 85,5 | 129 | 174 | 80,9 |
| Statistik | Trainings (%) | Test (%) |
|---|---|---|
| Richtig-Positiv-Rate (Empfindlichkeit oder Trennschärfe) | 84,2 | 75,5 |
| Falsch-Positiv-Rate (Fehler 1. Art) | 13,4 | 14,6 |
| Falsch-Negativ-Rate (Fehler 2. Art) | 15,8 | 24,5 |
| Richtig-Negativ-Rate (Spezifität) | 86,6 | 85,4 |
Wichtigstes Ergebnis: Konfusionsmatrix
- Richtig-Positiv-Rate (TPR): 84,2 % für die Trainingsdaten und 75,5 % für die Testdaten
- Falsch-Positiv-Rate (FPR): 13,4 % für die Trainingsdaten und 14,6 % für die Testdaten
- Falsch-Negativ-Rate (FNR): 15,8 % für die Trainingsdaten und 24,5 % für die Testdaten
- Richtig-Negativ-Rate (TNR): 86,6 % für die Trainingsdaten und 85,4 % für die Testdaten
Insgesamt beläuft sich %Richtig für die Trainingsdaten auf 85,5 % und für die Testdaten auf 80,9 %.
