Die A-posteriori-Wahrscheinlichkeit ist die Wahrscheinlichkeit, mit der Beobachtungen auf der Grundlage der Daten Gruppen zugewiesen werden. Die A-priori-Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass eine Beobachtung einer Gruppe angehört, bevor die Daten erfasst werden. Wenn Sie z. B. die Käufer eines bestimmten Autos klassifizieren, wissen Sie vielleicht bereits, dass 60 % der Käufer männlich und 40 % weiblich sind. Wenn Sie diese Wahrscheinlichkeiten kennen oder schätzen können, werden diese A-priori-Wahrscheinlichkeiten in die Diskriminanzanalyse einbezogen, um die A-posteriori-Wahrscheinlichkeiten zu berechnen. Wenn keine A-priori-Wahrscheinlichkeiten angegeben werden, nimmt Minitab eine gleiche Wahrscheinlichkeit für die Gruppen an.
Bei Annahme der Normalverteilung der Daten erhöht sich die lineare Diskriminanzfunktion um ln(pi), wobei pi die A-priori-Wahrscheinlichkeit von Gruppe i darstellt. Da die Beobachtungen den Gruppen nach der kleinsten verallgemeinerten Distanz oder äquivalent nach der größten linearen Diskriminanzfunktion zugewiesen werden, bewirkt dies, dass die A-posteriori-Wahrscheinlichkeit für eine Gruppe mit einer großen A-priori-Wahrscheinlichkeit vergrößert wird.
Hinweis
Durch Angabe von A-priori-Wahrscheinlichkeiten kann die Präzision der Ergebnisse erheblich beeinflusst werden. Untersuchen Sie, ob die ungleichen Anteile in den einzelnen Gruppen einen realen Unterschied in der tatsächlichen Grundgesamtheit angeben oder ob der Unterschied auf einen Stichprobenfehler zurückzuführen ist.
Angenommen, es liegen A-priori-Wahrscheinlichkeiten vor und fi(x) ist die gemeinsame Dichte für die Daten in der Gruppe i (wobei die Parameter der Grundgesamtheit durch die Stichprobenschätzwerte ersetzt werden).
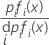
Die größte A-posteriori-Wahrscheinlichkeit entspricht dem höchsten Wert von ln [pifi(x)]
Wenn fi(x) die Normalverteilung ist, gilt Folgendes:
ln [pifi(x)] = –0,5 [di2(x) – 2 ln pi] – (eine Konstante)
Der Term in eckigen Klammern wird als verallgemeinerte quadrierte Distanz von x zu Gruppe i bezeichnet und durch di2(x) angegeben. Beachten Sie, dass
di2(x) = –2[mi' Sp–1 x – 0,5 mi' Sp–1mi + ln pi] + x' Sp–1x
Der Term in eckigen Klammern ist die lineare Diskriminanzfunktion. Der einzige Unterschied zum Fall ohne A-priori-Wahrscheinlichkeiten ist eine Änderung im konstanten Term. Beachten Sie, dass die größte A-posteriori-Wahrscheinlichkeit gleich der kleinsten verallgemeinerten Distanz ist, die wiederum der größten linearen Diskriminanzfunktion entspricht.
