Methoden und Formeln für Hauptkomponentenanalyse

Bei der Hauptkomponentenanalyse ermittelt Minitab zuerst die orthogonalen Eigenvektoren der Korrelations- oder Kovarianzmatrix der Variablen. Die Matrix der Hauptkomponenten ist das Produkt der Eigenvektormatrix und der Matrix der unabhängigen Variablen. Die erste Hauptkomponente erklärt den größten Prozentsatz der Gesamtstreuung in den Daten. Die zweite Hauptkomponente erklärt den zweitgrößten Prozentsatz der Gesamtstreuung in den Daten usw. Das Ziel der Hauptkomponentenanalyse besteht darin, den größtmöglichen Anteil der Streuung mit der kleinstmöglichen Anzahl von Komponenten zu erklären.

Die Koeffizienten für die Hauptkomponenten sind eindeutig (außer bei einem Vorzeichenwechsel), wenn die Eigenwerte eindeutig und nicht null sind. Wenn ein Eigenwert wiederholt wird, ist der durch alle Hauptkomponentenvektoren mit demselben Eigenwert „aufgespannte Raum“ eindeutig, die einzelnen Vektoren sind es jedoch nicht. Deswegen stimmen die von Minitab ausgegebenen Koeffizienten möglicherweise nicht mit den in der Literatur oder anderen Programmen angegebenen überein, obwohl die Eigenwerte (Varianzen der Komponenten) immer dieselben sind.

Wenn die Kovarianzmatrix über einen Rang r < p verfügt, wobei p die Anzahl der Variablen ist, sind p – r Eigenwerte gleich null. Die Eigenvektoren, die diesen Eigenwerten entsprechen, sind möglicherweise nicht eindeutig. Dies kann geschehen, wenn die Anzahl an Beobachtungen kleiner als p ist oder Multikollinearität vorliegt.

Eigenvektoren, die sich aus den Koeffizienten für die einzelnen Variablen zusammensetzen, sind die Gewichtungen für die einzelnen Variablen zur Berechnung der Werte (Scores) der Hauptkomponenten. Die Eigenvektoren werden als Spalten der orthogonalen Matrix in der Spektralzerlegung der Kovarianz- oder Korrelationsmatrix S oder R berechnet. Genauer ausgedrückt: Weil R symmetrisch ist, existiert eine orthogonale Matrix V, so dass V'RV = D oder äquivalent R = VDV', wobei D eine diagonale Matrix ist, deren Diagonalelemente die Eigenwerte sind. Die Eigenvektoren sind die Spalten von V. Die Eigenvektoren stammen aus R = V D V'.

Notation

Formel

Die Werte sind die linearen Kombinationen der ursprünglichen Variablen, die die Varianz in den Daten erklären.

Die Werte werden folgendermaßen berechnet: Z = YV

Notation

Formel

Bei den Eigenwerten handelt es sich um die Diagonalelemente der diagonalen Matrix in der Spektralzerlegung der Kovarianz- oder Korrelationsmatrix (siehe Thema „Eigenvektoren“). Die Eigenwerte entsprechen auch den Stichprobenvarianzen der Hauptkomponenten Z = V Y.

Notation

Formel

Der Anteil an der Stichprobenvarianz, der durch die k-te Hauptkomponente erklärt wird, berechnet sich wie folgt:

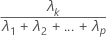
Notation

Begriff	Beschreibung
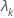	k-ter Eigenwert
p	Anzahl der Variablen

Formel

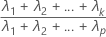
Notation

Begriff	Beschreibung
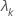	k-ter Eigenwert
p	Anzahl der Variablen

Formel

Die Mahalanobis-Distanz ist ein Maß für den Abstand zwischen einem bestimmten Punkt im multivariaten Raum und dem Gesamtmittelwert (dem Zentroiden); die Berechnung dieses Maßes beruht auf der Kovarianzstruktur der Daten.

Minitab zeichnet im Diagramm der Ausreißer eine Referenzlinie, durch die sich Ausreißer mit großen Mahalanobis-Distanzen erkennen lassen. Die Referenzlinie wird durch folgende Formel definiert:

Wenn n–p–1 0 ist, zeigt Minitab das Diagramm der Ausreißer ohne die Referenzlinie an.

Notation

Begriff	Beschreibung
Yi	Vektor der Datenwerte in Zeile i
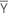	Mittelwertvektor
S–1	Inverse der Kovarianzmatrix
p	Anzahl der Variablen
n	Anzahl der nicht fehlenden Zeilen