Spaltenbeiträge für Multiple Korrespondenzanalyse

Die Spaltenprofile liegen in einem d-dimensionalen Raum. Dieser Raum wird von dem vollständigen Satz der d Hauptachsen aufgespannt. Angenommen, g_j1, g_j2, g_j3, ..., g_jd sind die Koordinaten von Spaltenprofil j auf den Hauptachsen. Diese Koordinaten werden als Hauptkoordinaten in Spalten bezeichnet. Die k-te Hauptkoordinate für das Spaltenprofil j ist g_jk.

Der beste k-dimensionale Unterraum wird von den ersten k Hauptachsen aufgespannt. Wenn Spaltenprofil j auf den besten k-dimensionalen Unterraum projiziert wird, sind g_j1, ..., g_jk die Hauptkoordinaten in Spalten für das Profil in diesem Unterraum.

Die Korrelation zwischen Spaltenprofil i und Hauptkomponente k wird folgendermaßen berechnet:

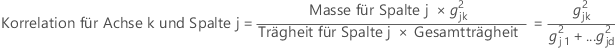
Minitab berechnet die relative Trägheit für jede Spalte. Die absolute Trägheit ist das Produkt aus der relativen Trägheit und der Gesamtträgheit.

Die Summe der Korrelationen für Spalte j über alle Hauptkomponenten beträgt 1. Die Summe über die ersten k Hauptkoordinaten entspricht der Qualität für das Spaltenprofil j und dem besten k-dimensionalen Unterraum.

Notation

Die Trägheit in einer Zelle wird wie folgt berechnet:

Die Summe aller Zellenträgheiten ist die Gesamtträgheit für die Tabelle, die gelegentlich einfach als Trägheit bezeichnet wird.

Die relative Trägheit für eine Zelle wird wie folgt berechnet:

Die Spaltenprofile liegen in einem c-dimensionalen Raum. Die Hauptkomponenten, auch als Hauptachsen bezeichnet, spannen Unterräume mit weniger Dimensionen auf. Als erste Hauptachse wird der Vektor im c-dimensionalen Raum ausgewählt, der den größten Teil der Gesamtträgheit erklärt. Die erste Hauptachse spannt daher den besten eindimensionalen Unterraum auf (also den, der gemäß eines geeigneten Maßes am nächsten an den Profilen liegt). Als zweite Hauptachse wird der Vektor im c-dimensionalen Raum ausgewählt, der den größten Teil der verbleibenden Trägheit erklärt. Die ersten zwei Hauptachsen spannen also den besten zweidimensionalen Unterraum auf. Als dritte Hauptachse wird der Vektor im c-dimensionalen Raum ausgewählt, der den größten Teil der nach Abzug der durch die ersten beiden Achsen erklärten Trägheit verbleibenden Trägheit erklärt. Die ersten drei Hauptachsen spannen also den besten dreidimensionalen Unterraum auf usw.

Sei d = der kleinere der beiden Werte (r – 1) und (c – 1). Die Spaltenprofile liegen tatsächlich in einem d-dimensionalen Unterraum des vollständigen c-dimensionalen Raums (bzw. des vollständigen r-dimensionalen Raums). Daher sind maximal d Hauptachsen vorhanden.

Die Qualität für das Spaltenprofil j und der beste k-dimensionale Unterraum werden wie folgt berechnet:

Die Qualität ist immer eine Zahl zwischen 0 und 1, wobei höhere Zahlen bessere Approximationen angeben.

Notation

Jede Spalte trägt zur Trägheit jeder Achse bei. Der Beitrag von Spalte j zu Achse k, ausgedrückt als Prozentsatz der Trägheit für Achse k, wird folgendermaßen berechnet:

Die Summe der Beiträge für Hauptachse k über alle Spalten j beträgt 1.

Notation

Die Masse für Spalte j wird wie folgt berechnet:

Der Vektor von c Spaltenmassen ist gleich dem durchschnittlichen Spaltenprofil.

Die standardisierten Koordinaten in Spalten für die Komponente k stellen den Quotienten aus den Hauptkoordinaten für die Komponente k und der Quadratwurzel der k-ten Trägheit dar.