In diesem Thema
Korrelationsmatrix
Die Korrelationsmatrix zeigt die Pearson-Korrelationswerte, die den Grad der linearen Beziehung zwischen den einzelnen Item- oder Variablenpaaren messen. Die Korrelation kann Werte von –1 bis +1 annehmen. In der Praxis weisen Items jedoch meist positive Korrelationen auf. Wenn zwei Items tendenziell gleichzeitig zu- bzw. abnehmen, ist der Korrelationswert positiv.
Interpretation
Mit der Korrelationsmatrix können Sie die Stärke und Richtung der Beziehung zwischen zwei Items oder Variablen untersuchen. Hohe, positive Korrelationswerte weisen darauf hin, dass die Items dieselbe Fähigkeit oder dasselbe Merkmal messen. Wenn die Items nicht stark korrelieren, messen sie möglicherweise verschiedene Merkmale oder sind nicht klar definiert.
Variablen mit Korrelationswerten über 0,7 werden häufig als stark korrelierend bezeichnet. Welcher Richtwert am besten geeignet ist, hängt jedoch auch von den Standards in Ihrem Fachgebiet und der Anzahl der Items in der Analyse ab.
Korrelationsmatrix
| Item 1 | Item 2 | |
|---|---|---|
| Item 2 | 0,903 | |
| Item 3 | 0,867 | 0,864 |
In diesen Ergebnissen sind alle Items stark miteinander korreliert. Item 1 und Item 2 weisen eine positive lineare Korrelation von 0,903 auf. Item 1 und Item 3 weisen eine positive lineare Korrelation von 0,867 auf, und Item 2 und Item 3 weisen eine positive lineare Korrelation von 0,864 auf. Diese Items scheinen daher dasselbe Merkmal zu messen.
Kovarianzmatrix
Die Kovarianzmatrix zeigt die Kovarianzwerte an, mit denen die lineare Beziehung zwischen den einzelnen Item- oder Variablenpaaren gemessen wird. Positive Kovarianzwerte geben an, dass überdurchschnittliche Werte einer Variablen mit überdurchschnittlichen Werten der anderen Variablen und unterdurchschnittliche Werte einer Variablen mit unterdurchschnittlichen Werten der anderen Variablen assoziiert sind. Negative Kovarianzwerte geben an, dass überdurchschnittliche Werte einer Variablen mit unterdurchschnittlichen Werten der anderen Variablen assoziiert sind.
Im Gegensatz zum Korrelationskoeffizienten ist die Kovarianz nicht standardisiert. Daher können Kovarianzwerte von der negativen Unendlichkeit bis zur positiven Unendlichkeit reichen und schwierig zu interpretieren sein. Um die lineare Beziehung zwischen den einzelnen Item- oder Variablenpaaren leichter interpretieren zu können, verwenden Sie die Korrelationsmatrix.
Mittelwert
Der Mittelwert ist die Summe der Beobachtungen dividiert durch die Anzahl der Beobachtungen. Minitab berechnet den Mittelwert für jedes Item und den Gesamtmittelwert. Der Item-Mittelwert ist die Summe aller Werte für ein Item dividiert durch die Anzahl der Werte für dieses Item. Der Gesamtmittelwert ist die Summe aller Item-Mittelwerte.
Interpretation
Verwenden Sie den Item-Mittelwert, um die Werte für jedes Item oder jede Variable mit einem einzelnen Wert zu beschreiben, der das Zentrum der Daten darstellt.
Item- und Gesamtstatistik
| Variable | Anzahl gesamt | Mittelwert | StdAbw |
|---|---|---|---|
| Item 1 | 50 | 3,1600 | 1,2675 |
| Item 2 | 50 | 2,8400 | 1,3607 |
| Item 3 | 50 | 2,9400 | 1,3463 |
| Gesamt | 50 | 8,9400 | 3,8087 |
In diesen Ergebnissen ist der Mittelwert von Item 1 am höchsten (3,16) und der Mittelwert von Item 2 am niedrigsten (2,84). Der Gesamtmittelwert ist die Summe der Mittelwerte für alle 3 Items.
StdAbw
Die Standardabweichung (StdAbw) ist ein Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Minitab berechnet die Standardabweichung der Werte für jedes Item bzw. jede Variable sowie die Summe der Standardabweichungen.
Interpretation
Verwenden Sie die Standardabweichung für die Items, um festzustellen, wie breit die Werte um den Mittelwert jedes Items gestreut sind.
Item- und Gesamtstatistik
| Variable | Anzahl gesamt | Mittelwert | StdAbw |
|---|---|---|---|
| Item 1 | 50 | 3,1600 | 1,2675 |
| Item 2 | 50 | 2,8400 | 1,3607 |
| Item 3 | 50 | 2,9400 | 1,3463 |
| Gesamt | 50 | 8,9400 | 3,8087 |
In diesen Ergebnissen weisen die Werte für Item 2 die höchste Standardabweichung auf (1,3607). Dies deutet darauf hin, dass die Werte für Item 2 die größte Streuung aller drei Items aufweisen. Item 1 weist die niedrigste Standardabweichung (1,2675) und somit die geringste Streuung der Werte auf. Die Gesamtstandardabweichung ist die Summe der Standardabweichungen für alle drei Items.
Cronbach-Alpha
Das Cronbach-Alpha ist eine Maßzahl für die innere Konsistenz, die anhand der Stichprobenvarianz, der Gesamtwerte und der Anzahl der Items berechnet wird.
Interpretation
Verwenden Sie das Cronbach-Alpha, um zu beurteilen, wie konsistent mehrere Items in einer Umfrage oder einem Test dieselbe Fähigkeit oder dasselbe Merkmal messen. Höhere Werte des Cronbach-Alpha deuten auf eine höhere innere Konsistenz hin. Ein häufig verwendeter Richtwert ist 0,7. Wenn das Cronbach-Alpha mehr als 0,7 beträgt, ist dies in der Regel ein Anzeichen dafür, dass die Umfrage- oder Test-Items dieselbe Fähigkeit oder dasselbe Merkmal messen. Wenn das Cronbach-Alpha weniger als 0,7 beträgt, messen die Items möglicherweise nicht zuverlässig genug dieselbe Fähigkeit oder dasselbe Merkmal, um zu schlussfolgern, dass wenigsten einige Items dasselbe Merkmal messen. Welcher Richtwert am besten geeignet ist, hängt jedoch auch von den Standards in Ihrem Fachgebiet und der Anzahl der Items in der Analyse ab.
Cronbach-Alpha
| Alpha |
|---|
| 0,9550 |
In diesen Ergebnissen beträgt der allgemeine Wert für das Cronbach-Alpha 0,955. Der Wert ist größer als der gängige Richtwert von 0,7 und weist darauf hin, dass mit den Items dasselbe Merkmal gemessen wird.
Kor. Gesamtmittelwert
Der korrigierte Gesamtmittelwert ist die Summe aller Item-Mittelwerte ohne den Mittelwert des ausgelassenen Items.
Interpretation
Verwenden Sie den korrigierten Gesamtmittelwert, um festzustellen, wie sich der Wert des Gesamtmittelwerts ändert, wenn ein Item aus der Analyse entfernt wird.
Statistik der ausgelassenen Items
| Ausgelassene Variable | Kor. Gesamtmittelwert | Kor. Gesamt-StdAbw | Für Item kor. Gesamtkorr. | Quadrierte multiple Korr. | Cronbach-Alpha |
|---|---|---|---|---|---|
| Item 1 | 5,780 | 2,613 | 0,9166 | 0,8447 | 0,9268 |
| Item 2 | 6,100 | 2,525 | 0,9134 | 0,8413 | 0,9277 |
| Item 3 | 6,000 | 2,563 | 0,8870 | 0,7869 | 0,9476 |
In diesen Ergebnissen beträgt der korrigierte Gesamtmittelwert 5,780, wenn Item 1 aus der Analyse ausgelassen wird. Das heißt, die Summe des Mittelwerts von Item 2 und des Mittelwerts von Item 3 beträgt 5,780.
Kor. Gesamt-StdAbw
Die korrigierte Gesamtstandardabweichung entspricht der Standardabweichung des Gesamtwerts nach Auslassung eines Items.
Interpretation
Verwenden Sie die korrigierte Gesamtstandardabweichung, um festzustellen, wie sich der Wert der Gesamtstandardabweichung ändert, wenn ein Item aus der Analyse entfernt wird.
Statistik der ausgelassenen Items
| Ausgelassene Variable | Kor. Gesamtmittelwert | Kor. Gesamt-StdAbw | Für Item kor. Gesamtkorr. | Quadrierte multiple Korr. | Cronbach-Alpha |
|---|---|---|---|---|---|
| Item 1 | 5,780 | 2,613 | 0,9166 | 0,8447 | 0,9268 |
| Item 2 | 6,100 | 2,525 | 0,9134 | 0,8413 | 0,9277 |
| Item 3 | 6,000 | 2,563 | 0,8870 | 0,7869 | 0,9476 |
In diesen Ergebnissen beträgt die korrigierte Gesamtstandardabweichung 2,613, wenn Item 1 aus der Analyse ausgelassen wird.
Für Item kor. Gesamtkorr.
Die für das Item korrigierte Gesamtkorrelation ist die Korrelation zwischen den Werten eines ausgelassenen Items und den Gesamtwerten aller anderen Items. Obwohl die Werte der für das Item korrigierten Gesamtkorrelation theoretisch von –1 bis 1 reichen können, bewegen sich die Werte in der Praxis üblicherweise zwischen 0 und 1.
Interpretation
Mit der für das Item korrigierten Gesamtkorrelation können Sie beurteilen, ob das Entfernen eines Items aus der Analyse die innere Konsistenz verbessert. Ein hoher Wert der für das Item korrigierten Gesamtkorrelation (näher an 1) deutet darauf hin, dass das ausgelassene Item dasselbe Merkmal misst wie die anderen Items. Wenn ein ausgelassenes Item einen niedrigen Wert für die für das Item korrigierte Gesamtkorrelation, einen niedrigen Wert für die quadrierte multiple Korrelation sowie einen wesentlich höheren Wert des Cronbach-Alpha aufweist, sollten Sie erwägen, dieses Item aus der Umfrage oder dem Test zu entfernen, um die innere Konsistenz zu verbessern.
Statistik der ausgelassenen Items
| Ausgelassene Variable | Kor. Gesamtmittelwert | Kor. Gesamt-StdAbw | Für Item kor. Gesamtkorr. | Quadrierte multiple Korr. | Cronbach-Alpha |
|---|---|---|---|---|---|
| Item 1 | 5,780 | 2,613 | 0,9166 | 0,8447 | 0,9268 |
| Item 2 | 6,100 | 2,525 | 0,9134 | 0,8413 | 0,9277 |
| Item 3 | 6,000 | 2,563 | 0,8870 | 0,7869 | 0,9476 |
In diesen Ergebnissen ist die für das Item korrigierte Gesamtkorrelation für Item 1 gleich 0,9166. Die für das Item korrigierte Gesamtkorrelation für Item 2 beträgt 0,9134. Die für das Item korrigierte Gesamtkorrelation für Item 3 beträgt 0,887. Da die für das Item korrigierte Gesamtkorrelation für alle Items gleichmäßig hoch ist, deutet dies darauf hin, dass alle Items dasselbe Merkmal messen.
Quadrierte multiple Korr.
Die quadrierte multiple Korrelation ist der Determinationskoeffizient (R2), wenn eine Regression des ausgelassenen Items auf die verbleibenden Items durchgeführt wird. Die Werte reichen von 0 bis 1.
Interpretation
Verwenden Sie die Werte der quadrierten multiplen Korrelation, um zu beurteilen, ob das Entfernen eines Items aus der Analyse die innere Konsistenz verbessert. Ein hoher Wert für die quadrierte multiple Korrelation (näher an 1) deutet darauf hin, dass das ausgelassene Item dasselbe Merkmal misst wie die anderen Items. Wenn ein ausgelassenes Item einen niedrigen Wert für die quadrierte multiple Korrelation, einen niedrigen Wert für die für das Item korrigierte Gesamtkorrelation sowie einen wesentlich höheren Wert des Cronbach-Alpha aufweist, sollten Sie erwägen, dieses Item aus der Umfrage oder dem Test zu entfernen, um die innere Konsistenz zu verbessern.
Statistik der ausgelassenen Items
| Ausgelassene Variable | Kor. Gesamtmittelwert | Kor. Gesamt-StdAbw | Für Item kor. Gesamtkorr. | Quadrierte multiple Korr. | Cronbach-Alpha |
|---|---|---|---|---|---|
| Item 1 | 5,780 | 2,613 | 0,9166 | 0,8447 | 0,9268 |
| Item 2 | 6,100 | 2,525 | 0,9134 | 0,8413 | 0,9277 |
| Item 3 | 6,000 | 2,563 | 0,8870 | 0,7869 | 0,9476 |
In diesen Ergebnissen beträgt die quadrierte Mehrfachkorrelation für Item 1 0,9166. Die quadrierte Mehrfachkorrelation für Item 2 beträgt 0,8413. Die quadrierte Mehrfachkorrelation für Item 3 beträgt 0,7869. Da die quadrierte multiple Korrelation für alle Items gleichmäßig hoch ist, deutet dies darauf hin, dass alle Items dasselbe Merkmal messen.
Cronbach-Alpha (für ein ausgelassenes Item)
Das Cronbach-Alpha für ein ausgelassenes Item entspricht dem Cronbach-Alpha für die verbleibenden Items, nachdem ein Item aus der Analyse entfernt wurde. Das Cronbach-Alpha ist eine Maßzahl für die innere Konsistenz, die anhand der Stichprobenvarianz, der Gesamtwerte und der Anzahl der Items berechnet wird.
Interpretation
Anhand des Cronbach-Alpha für ausgelassene Items können Sie beurteilen, ob das Entfernen eines Items aus der Analyse die innere Konsistenz verbessert. Weitgehend einheitliche Werte des Cronbach-Alpha für alle ausgelassenen Items deuten darauf hin, dass alle Items dasselbe Merkmal messen. Ein wesentlich höherer Wert des Cronbach-Alpha für ein bestimmtes ausgelassenes Item deutet darauf hin, dass dieses möglicherweise nicht dasselbe Merkmal misst wie die anderen Items. Wenn ein ausgelassenes Item einen niedrigen Wert für die quadrierte multiple Korrelation, einen niedrigen Wert für die für das Item korrigierte Gesamtkorrelation sowie einen wesentlich höheren Wert des Cronbach-Alpha aufweist, sollten Sie erwägen, dieses Item aus der Umfrage oder dem Test zu entfernen, um die innere Konsistenz zu verbessern.
Statistik der ausgelassenen Items
| Ausgelassene Variable | Kor. Gesamtmittelwert | Kor. Gesamt-StdAbw | Für Item kor. Gesamtkorr. | Quadrierte multiple Korr. | Cronbach-Alpha |
|---|---|---|---|---|---|
| Item 1 | 5,780 | 2,613 | 0,9166 | 0,8447 | 0,9268 |
| Item 2 | 6,100 | 2,525 | 0,9134 | 0,8413 | 0,9277 |
| Item 3 | 6,000 | 2,563 | 0,8870 | 0,7869 | 0,9476 |
In diesen Ergebnissen beträgt das Cronbach-Alpha 0,9268, wenn Item 1 ausgelassen wird. Wenn Item 2 ausgelassen wird, beträgt das Cronbach-Alpha 0,9277. Wenn Item 3 ausgelassen wird, beträgt das Cronbach-Alpha 0,9476. Da das Cronbach-Alpha für alle ausgelassenen Items ähnlich ist, deutet dies darauf hin, dass alle Items dasselbe Merkmal messen.
Matrixplot
Das Matrixplot ist ein Feld von Streudiagrammen. Jedes Streudiagramm in der Matrix stellt die Werte für ein Item-Paar auf der x- und der y-Achse dar.
Interpretation
Verwenden Sie das Diagramm, um die Beziehung zwischen den einzelnen Kombinationen von Items und Variablen visuell auszuwerten.
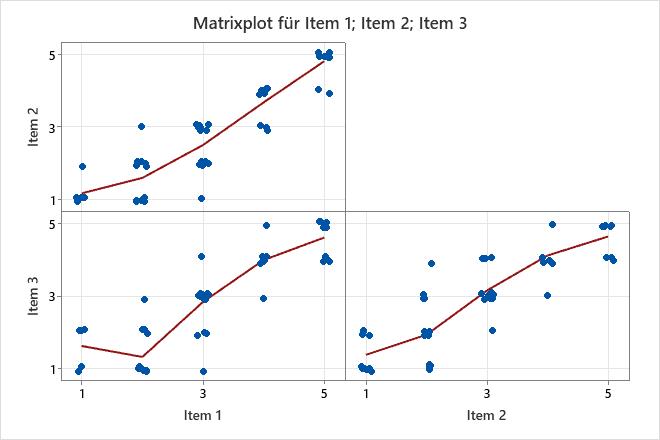
Dieses Matrixplot weist darauf hin, dass alle Item-Paare eine positive lineare Beziehung aufweisen.
