In diesem Thema
Faktorladungen
Die Faktorladungen geben an, wie stark ein Faktor eine bestimmte Variable erklärt. Die Ladungen können Werte von –1 bis 1 annehmen.
Minitab berechnet die nicht rotierten Faktorladungen. Wenn Sie für die Analyse eine Rotationsmethode auswählen, berechnet Minitab die rotierten Faktorladungen.
Interpretation
Untersuchen Sie das Ladungsmuster, um den Faktor zu ermitteln, der die einzelnen Variablen am stärksten beeinflusst. Je näher die Ladung am Extremwert –1 oder 1 liegt, desto stärker beeinflusst der Faktor die Variable. Eine Ladung nahe 0 gibt an, dass die Variable durch den Faktor nur schwach beeinflusst wird. Manche Variablen können eine hohe Ladung bei mehreren Faktoren aufweisen.
Nicht rotierte Faktorladungen sind oft schwierig zu interpretieren. Die Faktorrotation vereinfacht die Ladungsstruktur und ermöglicht oft eine deutlichere Unterscheidung sowie eine einfachere Interpretation der Faktoren. Möglicherweise sind jedoch nicht alle Rotationsmethoden für alle Fälle gleich gut geeignet. Versuchen Sie es mit verschiedenen Rotationen, und verwenden Sie die, die die am besten interpretierbaren Ergebnisse liefert. Sie können die rotierten Ladungen auch sortieren, um die Ladungen innerhalb eines Faktors noch differenzierter zu beurteilen.
- Unternehmenseignung (0,778), Stelleneignung (0,844) und Potenzial (0,645) weisen große positive Ladungen für Faktor 1 auf, dieser Faktor beschreibt also die Eignung des Mitarbeiters und dessen Potenzial für Wachstum im Unternehmen.
- Auftreten (0,730), Sympathie (0,615) und Selbstbewusstsein (0,743) weisen große positive Ladungen für Faktor 2 auf, dieser Faktor beschreibt also persönliche Eigenschaften.
- Kommunikation (0,802) und Disziplin (0,889) weisen große positive Ladungen für Faktor 3 auf, dieser Faktor beschreibt also die Arbeitsweise.
- Anschreiben (0,947) und Lebenslauf (0,789) weisen große positive Ladungen für Faktor 4 auf, dieser Faktor beschreibt also schriftliche Fähigkeiten.
Nicht rotierte Faktorladungen und Kommunalitäten
| Variable | Faktor1 | Faktor2 | Faktor3 | Faktor4 | Kommunalität |
|---|---|---|---|---|---|
| Studienleistungen | 0,380 | 0,455 | 0,340 | 0,259 | 0,534 |
| Auftreten | 0,359 | 0,530 | -0,040 | 0,523 | 0,685 |
| Kommunikation | 0,465 | 0,660 | -0,377 | -0,023 | 0,795 |
| Unternehmenseignung | 0,523 | 0,677 | 0,266 | -0,253 | 0,866 |
| Erfahrung | 0,508 | 0,194 | 0,450 | 0,232 | 0,553 |
| Stelleneignung | 0,532 | 0,632 | 0,415 | -0,201 | 0,895 |
| Anschreiben | 0,992 | -0,094 | -0,012 | -0,007 | 0,994 |
| Sympathie | 0,412 | 0,529 | 0,032 | 0,377 | 0,593 |
| Disziplin | 0,406 | 0,761 | -0,424 | -0,055 | 0,926 |
| Potenzial | 0,446 | 0,548 | 0,431 | 0,172 | 0,714 |
| Lebenslauf | 0,850 | 0,040 | 0,096 | 0,283 | 0,814 |
| Selbstbewusstsein | 0,293 | 0,575 | 0,083 | 0,506 | 0,679 |
| Varianz | 3,6320 | 3,3193 | 1,0883 | 1,0095 | 9,0491 |
| % Var | 0,303 | 0,277 | 0,091 | 0,084 | 0,754 |
Rotierte Faktorladungen und Kommunalitäten
| Variable | Faktor1 | Faktor2 | Faktor3 | Faktor4 | Kommunalität |
|---|---|---|---|---|---|
| Studienleistungen | 0,481 | 0,510 | 0,086 | 0,188 | 0,534 |
| Auftreten | 0,140 | 0,730 | 0,319 | 0,175 | 0,685 |
| Kommunikation | 0,203 | 0,280 | 0,802 | 0,181 | 0,795 |
| Unternehmenseignung | 0,778 | 0,165 | 0,445 | 0,189 | 0,866 |
| Erfahrung | 0,472 | 0,395 | -0,112 | 0,401 | 0,553 |
| Stelleneignung | 0,844 | 0,209 | 0,305 | 0,215 | 0,895 |
| Anschreiben | 0,219 | 0,052 | 0,217 | 0,947 | 0,994 |
| Sympathie | 0,261 | 0,615 | 0,321 | 0,208 | 0,593 |
| Disziplin | 0,217 | 0,285 | 0,889 | 0,086 | 0,926 |
| Potenzial | 0,645 | 0,492 | 0,121 | 0,202 | 0,714 |
| Lebenslauf | 0,214 | 0,365 | 0,113 | 0,789 | 0,814 |
| Selbstbewusstsein | 0,239 | 0,743 | 0,249 | 0,092 | 0,679 |
| Varianz | 2,5153 | 2,4880 | 2,0863 | 1,9594 | 9,0491 |
| % Var | 0,210 | 0,207 | 0,174 | 0,163 | 0,754 |
Kommunalität
Die Kommunalität ist der von den Faktoren erklärte Anteil an der Streuung für die einzelnen Variablen. Der Kommunalitätswert ist immer gleich, unabhängig davon, ob Sie für die Analyse nicht rotierte oder rotierte Faktorladungen verwenden.
Interpretation
Untersuchen Sie die Kommunalität, um zu beurteilen, wie gut die einzelnen Variablen von den Faktoren erklärt werden. Je näher die Kommunalität an 1 liegt, desto besser wird die Variable von den Faktoren erklärt. Sie können einen Faktor hinzufügen, wenn dieser bei bestimmten Variablen wesentlich zur besseren Anpassung beiträgt.
Nicht rotierte Faktorladungen und Kommunalitäten
| Variable | Faktor1 | Faktor2 | Faktor3 | Faktor4 | Kommunalität |
|---|---|---|---|---|---|
| Studienleistungen | 0,380 | 0,455 | 0,340 | 0,259 | 0,534 |
| Auftreten | 0,359 | 0,530 | -0,040 | 0,523 | 0,685 |
| Kommunikation | 0,465 | 0,660 | -0,377 | -0,023 | 0,795 |
| Unternehmenseignung | 0,523 | 0,677 | 0,266 | -0,253 | 0,866 |
| Erfahrung | 0,508 | 0,194 | 0,450 | 0,232 | 0,553 |
| Stelleneignung | 0,532 | 0,632 | 0,415 | -0,201 | 0,895 |
| Anschreiben | 0,992 | -0,094 | -0,012 | -0,007 | 0,994 |
| Sympathie | 0,412 | 0,529 | 0,032 | 0,377 | 0,593 |
| Disziplin | 0,406 | 0,761 | -0,424 | -0,055 | 0,926 |
| Potenzial | 0,446 | 0,548 | 0,431 | 0,172 | 0,714 |
| Lebenslauf | 0,850 | 0,040 | 0,096 | 0,283 | 0,814 |
| Selbstbewusstsein | 0,293 | 0,575 | 0,083 | 0,506 | 0,679 |
| Varianz | 3,6320 | 3,3193 | 1,0883 | 1,0095 | 9,0491 |
| % Var | 0,303 | 0,277 | 0,091 | 0,084 | 0,754 |
In diesen Ergebnissen wurden 4 Faktoren aus den 12 Variablen extrahiert. Die Kommunalitätswerte sind für alle Variablen hoch, was darauf hindeutet, dass die Variablen von den 4 Faktoren gut dargestellt werden. Beispielsweise erklären die 4 Faktoren 0,895 oder 89,5 % der Streuung bei der Stelleneignung.
Varianz
Die Streuung in den Daten, die von den einzelnen Faktoren erklärt wird. Wenn Sie die Faktoren mit Hilfe der Hauptkomponentenmethode extrahieren und die Ladungen nicht rotieren, ist die Varianz jedes Faktors gleich dessen Eigenwert. Durch eine Rotation ändert sich die Verteilung der Anteile an der Streuung, die von den einzelnen Faktoren erklärt wird, obwohl die durch alle Faktoren erklärte Gesamtstreuung gleich bleibt.
Interpretation
Untersuchen Sie die Varianz für jeden Faktor. Je höher die Varianz, desto mehr erklärt der Faktor die Streuung in den Daten. Wenn Sie nicht wissen, wie viele Faktoren Sie für die Analyse extrahieren sollen, verwenden Sie zur vorläufigen Beurteilung die Hauptkomponenten als Extraktionsmethode ohne Rotation und mit der Standardanzahl an Faktoren (womit die maximale Anzahl an Faktoren extrahiert wird). Definieren Sie dann die wichtigen Faktoren als diejenigen, bei denen die Varianz (der Eigenwert) einen bestimmten Wert überschreitet. Ein Kriterium ist z. B., alle Faktoren mit einem Eigenwert von mindestens 1 einzubinden. Eine weitere Methode ist die visuelle Untersuchung der Eigenwerte im Screeplot, um zu bestimmen, ab welchem Punkt die Eigenwerte nur noch geringfügige Änderungen aufweisen und gegen 0 tendieren. Weitere Informationen finden Sie im Thema zum Screeplot.
Nicht rotierte Faktorladungen und Kommunalitäten
| Variable | Faktor1 | Faktor2 | Faktor3 | Faktor4 | Faktor5 | Faktor6 | Faktor7 | Faktor8 |
|---|---|---|---|---|---|---|---|---|
| Studienleistungen | 0,726 | 0,336 | -0,326 | 0,104 | -0,354 | -0,099 | 0,233 | 0,147 |
| Auftreten | 0,719 | -0,271 | -0,163 | -0,400 | -0,148 | -0,362 | -0,195 | -0,151 |
| Kommunikation | 0,712 | -0,446 | 0,255 | 0,229 | -0,319 | 0,119 | 0,032 | 0,088 |
| Unternehmenseignung | 0,802 | -0,060 | 0,048 | 0,428 | 0,306 | -0,137 | -0,067 | 0,105 |
| Erfahrung | 0,644 | 0,605 | -0,182 | -0,037 | -0,092 | 0,317 | -0,209 | -0,102 |
| Stelleneignung | 0,813 | 0,078 | -0,029 | 0,365 | 0,368 | -0,067 | -0,025 | -0,032 |
| Anschreiben | 0,625 | 0,327 | 0,654 | -0,134 | 0,031 | 0,025 | 0,017 | -0,113 |
| Sympathie | 0,739 | -0,295 | -0,117 | -0,346 | 0,249 | 0,140 | 0,353 | -0,142 |
| Disziplin | 0,706 | -0,540 | 0,140 | 0,247 | -0,217 | 0,136 | -0,080 | -0,105 |
| Potenzial | 0,814 | 0,290 | -0,326 | 0,167 | -0,068 | -0,073 | 0,048 | -0,112 |
| Lebenslauf | 0,709 | 0,298 | 0,465 | -0,343 | -0,022 | -0,107 | 0,024 | 0,170 |
| Selbstbewusstsein | 0,719 | -0,262 | -0,294 | -0,409 | 0,175 | 0,179 | -0,159 | 0,230 |
| Varianz | 6,3876 | 1,4885 | 1,1045 | 1,0516 | 0,6325 | 0,3670 | 0,3016 | 0,2129 |
| % Var | 0,532 | 0,124 | 0,092 | 0,088 | 0,053 | 0,031 | 0,025 | 0,018 |
| Variable | Faktor9 | Faktor10 | Faktor11 | Faktor12 | Kommunalität |
|---|---|---|---|---|---|
| Studienleistungen | 0,097 | -0,142 | -0,026 | -0,031 | 1,000 |
| Auftreten | 0,082 | 0,016 | 0,020 | -0,038 | 1,000 |
| Kommunikation | 0,023 | 0,204 | 0,012 | -0,100 | 1,000 |
| Unternehmenseignung | -0,019 | -0,067 | 0,188 | -0,021 | 1,000 |
| Erfahrung | 0,121 | 0,039 | 0,077 | 0,009 | 1,000 |
| Stelleneignung | 0,146 | 0,066 | -0,176 | 0,008 | 1,000 |
| Anschreiben | -0,079 | -0,130 | -0,043 | -0,127 | 1,000 |
| Sympathie | 0,051 | 0,022 | 0,064 | 0,012 | 1,000 |
| Disziplin | -0,020 | -0,162 | -0,032 | 0,136 | 1,000 |
| Potenzial | -0,290 | 0,100 | -0,023 | 0,028 | 1,000 |
| Lebenslauf | 0,008 | 0,090 | 0,010 | 0,156 | 1,000 |
| Selbstbewusstsein | -0,098 | -0,061 | -0,065 | -0,047 | 1,000 |
| Varianz | 0,1557 | 0,1379 | 0,0851 | 0,0750 | 12,0000 |
| % Var | 0,013 | 0,011 | 0,007 | 0,006 | 1,000 |
Diese Analyse wurde mit der Hauptkomponentenmethode und den Standardeinstellungen (keine Rotation) durchgeführt. Bei den ersten vier Faktoren ist die Varianz (der Eigenwert) größer als 1. Die Eigenwerte ändern sich weniger deutlich, wenn mehr als 6 Faktoren verwendet werden. Also erklären 4 Faktoren den Großteil der Streuung in den Daten. Wiederholen Sie die Faktorenanalyse auf der Grundlage dieser vorläufigen Ergebnisse, extrahieren Sie nur 4 Faktoren, und experimentieren Sie mit verschiedenen Rotationen.
% Var
Die prozentuale Varianz (% Var) ist der Anteil an der Streuung in den Daten, der von den einzelnen Faktoren erklärt wird. Die Werte von % Var können von 0 (0 %) bis 1 (100 %) reichen.
Interpretation
Untersuchen Sie den Wert von % Var für jeden Faktor. Höhere Werte von % Var zeigen an, dass ein Faktor mehr Streuung erklärt. Sie können daher anhand der Werte von % Var bestimmen, welche Werte am wichtigsten sind.
Der Kommunalitätswert von % Var gibt die Streuung an, die insgesamt von allen Faktoren in der Analyse erklärt wird. Verwenden Sie diesen Wert, um festzustellen, ob die Anzahl der in der Analyse verwendeten Faktoren einen ausreichenden Betrag der Gesamtstreuung in den Daten erklärt.
Nicht rotierte Faktorladungen und Kommunalitäten
| Variable | Faktor1 | Faktor2 | Faktor3 | Faktor4 | Kommunalität |
|---|---|---|---|---|---|
| Studienleistungen | 0,380 | 0,455 | 0,340 | 0,259 | 0,534 |
| Auftreten | 0,359 | 0,530 | -0,040 | 0,523 | 0,685 |
| Kommunikation | 0,465 | 0,660 | -0,377 | -0,023 | 0,795 |
| Unternehmenseignung | 0,523 | 0,677 | 0,266 | -0,253 | 0,866 |
| Erfahrung | 0,508 | 0,194 | 0,450 | 0,232 | 0,553 |
| Stelleneignung | 0,532 | 0,632 | 0,415 | -0,201 | 0,895 |
| Anschreiben | 0,992 | -0,094 | -0,012 | -0,007 | 0,994 |
| Sympathie | 0,412 | 0,529 | 0,032 | 0,377 | 0,593 |
| Disziplin | 0,406 | 0,761 | -0,424 | -0,055 | 0,926 |
| Potenzial | 0,446 | 0,548 | 0,431 | 0,172 | 0,714 |
| Lebenslauf | 0,850 | 0,040 | 0,096 | 0,283 | 0,814 |
| Selbstbewusstsein | 0,293 | 0,575 | 0,083 | 0,506 | 0,679 |
| Varianz | 3,6320 | 3,3193 | 1,0883 | 1,0095 | 9,0491 |
| % Var | 0,303 | 0,277 | 0,091 | 0,084 | 0,754 |
In diesen Ergebnissen wird ein Anteil von 0,303 bzw. 30,3 % der Streuung in den Daten von Faktor 1 erklärt. Alle vier Faktoren zusammen erklären einen Anteil von 0,754 bzw. 75,4 % der Streuung in den Daten.
Gewichtungsfaktoren der Faktorwerte
Die Faktorkoeffizienten geben in einer Faktorenanalyse die relative Gewichtung der einzelnen Variablen in der Komponente an. Je größer der absolute Wert des Koeffizienten, desto wichtiger ist die entsprechende Variable bei der Berechnung der Komponente. Minitab verwendet die Faktorkoeffizienten zur Berechnung der Faktorwerte, bei denen es sich um geschätzte Werte der Faktoren handelt. Minitab berechnet Faktorwerte durch Multiplikation der Gewichtungsfaktoren der Faktorwerte (aufgeführt unter Faktor1, Faktor2 usw.) mit den Daten, nachdem diese durch Subtraktion der Mittelwerte skaliert und zentriert wurden.
Interpretation
- Sie können das Verhalten von Beobachtungen untersuchen.
- Sie können sie in anderen Analysen verwenden, z.B. in der Regression oder MANOVA.
Hinweis
Sie müssen die Variablen standardisieren, um die geschätzten Koeffizienten zur Berechnung der Faktorwerte verwenden zu können.
Screeplot
Das Screeplot veranschaulicht die Anzahl der Faktoren im Vergleich zu deren Eigenwert. Die Eigenwerte werden im Screeplot vom höchsten zum niedrigsten Wert angeordnet. Wenn keine Rotation erfolgt, sind die Eigenwerte der Korrelationsmatrix gleich den Varianzen der Faktoren.
Um das Screeplot anzuzeigen, müssen Sie auf Grafiken klicken und das Screeplot auswählen, wenn Sie die Analyse durchführen.
Interpretation
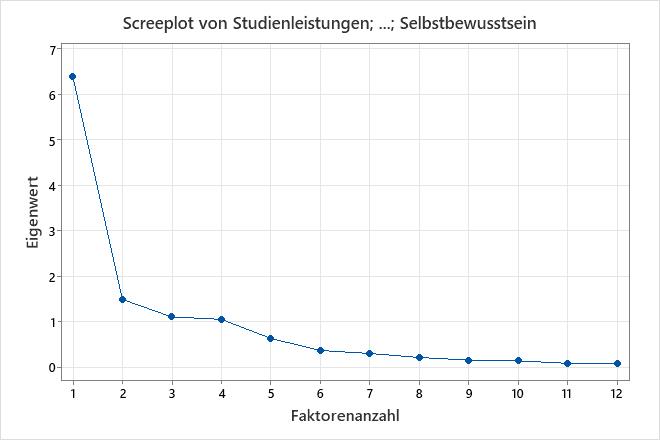
Das Screeplot zeigt, dass die ersten vier Faktoren den Großteil der Gesamtstreuung in den Daten erklären (angegeben durch die Eigenwerte). Die Eigenwerte der ersten vier Faktoren sind alle größer als 1. Die verbleibenden Faktoren erklären einen sehr kleinen Anteil der Streuung und sind wahrscheinlich unwichtig.
Scoreplot
Im Scoreplot werden die Werte des zweiten Faktors im Vergleich zu den Werten des ersten Faktors grafisch dargestellt.
Um das Scoreplot anzuzeigen, müssen Sie auf Grafiken klicken und das Scoreplot auswählen, wenn Sie die Analyse durchführen.
Interpretation
Wenn die ersten beiden Faktoren den größten Teil der Varianz in den Daten erklären, können Sie mit Hilfe des Scoreplots die Datenstruktur untersuchen sowie Cluster, Ausreißer und Trends erkennen. Gruppierungen von Daten im Diagramm können auf zwei oder mehr separate Verteilungen in den Daten hinweisen. Wenn die Daten einer Normalverteilung folgen und keine Ausreißer vorliegen, sind die Punkte nach einem zufälligen Muster um den Wert 0 verteilt.
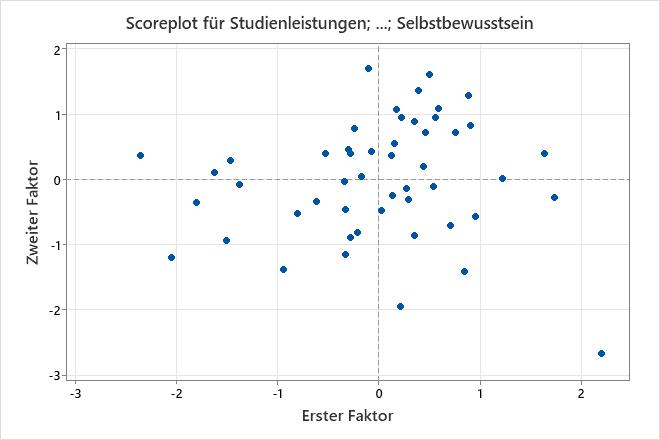
In diesem Scoreplot scheinen die Daten normalverteilt zu sein, und es sind keine extremen Ausreißer erkennbar. Möglicherweise empfiehlt es sich jedoch, den Datenwert unten rechts im Diagramm näher zu untersuchen, der etwas weiter entfernt von den übrigen Datenwerten liegt.
Tipp
Um den berechneten Wert für jede Beobachtung anzuzeigen, zeigen Sie mit dem Mauszeiger auf einen beliebigen Punkt im Diagramm. Um Scoreplots für andere Faktoren zu erstellen, speichern Sie die Werte, und verwenden Sie .
Ladungsdiagramm
Im Ladungsdiagramm werden die rotierten Faktorladungen jeder Variablen für den ersten Faktor im Vergleich zu den rotierten Faktorladungen jeder Variablen für den zweiten Faktor dargestellt.
Um das Ladungsdiagramm anzuzeigen, müssen Sie auf Grafiken klicken und das Ladungsdiagramm auswählen, wenn Sie die Analyse durchführen.
Interpretation
Verwenden Sie das Ladungsdiagramm, um festzustellen, welche Variablen den größten Effekt auf die Faktoren haben. Die Ladungen können Werte von –1 bis 1 annehmen. Je näher die Ladung am Extremwert –1 oder 1 liegt, desto stärker beeinflusst der Faktor die Variable. Eine Ladung nahe 0 gibt an, dass die Variable durch den Faktor nur schwach beeinflusst wird. Eine Untersuchung der Ladungen ist auch bei der Charakterisierung der einzelnen Faktoren in Hinblick auf die Variablen hilfreich. Nachdem Sie die Anzahl der Faktoren ermittelt haben, sollten Sie verschiedene Rotationen testen, um die Ladungen der Faktoren leichter interpretieren zu können.
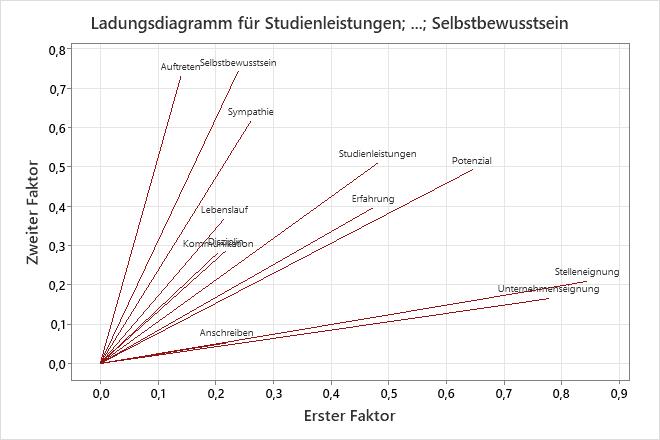
Für dieses Ladungsdiagramm wurde eine Varimax-Rotation der Daten vorgenommen, wodurch die ersten zwei Faktoren leichter zu interpretieren sind. „Stelleneignung“ und „Unternehmenseignung“ weisen große positive Ladungen für Faktor 1 auf, dieser Faktor beschreibt also die Eignung eines Bewerbers für die Stelle. „Auftreten“, „Sympathie“ und „Selbstbewusstsein“ weisen große positive Ladungen für Faktor 2 auf, dieser Faktor beschreibt also die persönlichen Eigenschaften eines Bewerbers.
Biplot
Das Biplot wird über das Scoreplot und das Ladungsdiagramm gelegt.
Um das Biplot anzuzeigen, müssen Sie auf Grafiken klicken und das Biplot auswählen, wenn Sie die Analyse durchführen.
Interpretation
Verwenden Sie das Biplot, um die Datenstruktur und die Ladungen der ersten beiden Faktoren in einer Grafik zu untersuchen. Minitab stellt die Werte des zweiten Faktors im Vergleich zu den Werten des ersten Faktors sowie die Ladungen für beide Faktoren grafisch dar.
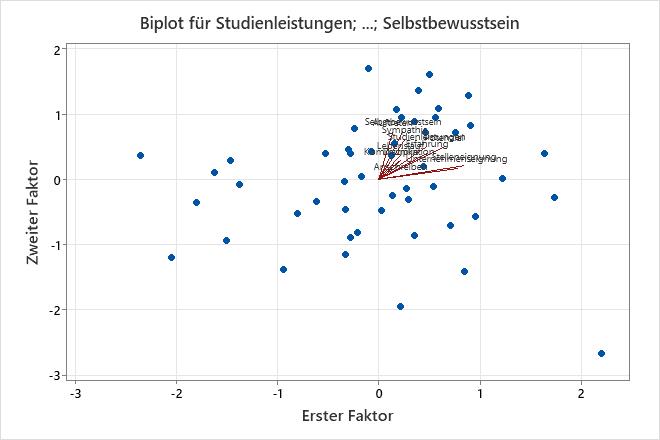
- Die Daten scheinen normalverteilt zu sein, und es sind keine extremen Ausreißer erkennbar. Möglicherweise empfiehlt es sich jedoch, den Datenwert unten rechts im Diagramm näher zu untersuchen, der etwas weiter entfernt von den übrigen Datenwerten liegt.
- „Stelleneignung“ und „Unternehmenseignung“ weisen große positive Ladungen für Faktor 1 auf, dieser Faktor beschreibt also die Eignung eines Bewerbers für die Stelle.
- Auftreten“, „Sympathie“ und „Selbstbewusstsein“ weisen große positive Ladungen für Faktor 2 auf, dieser Faktor beschreibt also die persönlichen Eigenschaften eines Bewerbers.
