Was ist ein faktorieller Versuchsplan?
Ein faktorieller Versuchsplan ist ein Typ von Versuchsplan, mit dem Sie die möglichen Auswirkungen einer Reihe von Faktoren auf eine Antwortvariable untersuchen können. Wenn Sie beim Ausführen eines Experiments statt der Stufe lediglich eines Faktors die Stufen aller Faktoren gleichzeitig ändern, können Sie die Wechselwirkungen zwischen den Faktoren untersuchen.
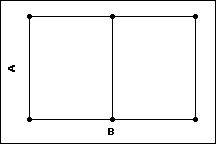
Zwei-Faktor-Versuchsplan
- 2 Stufen von Faktor A
- 3 Stufen von Faktor B
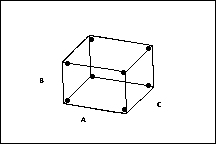
Drei-Faktor-Versuchsplan
2 Stufen je Faktor
Man unterscheidet zwischen vollfaktoriellen und teilfaktoriellen Versuchsplänen.
Hinweis
Wenn Sie über einen faktoriellen Versuchsplan mit Zentralpunkten verfügen, können Sie prüfen, ob in der Wirkungsfläche eine Krümmung vorhanden ist. Die Auswirkung dieser Krümmung kann jedoch nur am Zentralpunkt modelliert werden. Sie können also lediglich die angepassten Werte an den Eckpunkten und dem Zentralpunkt des Versuchsplans berechnen, und daher können Sie kein Konturdiagramm erstellen. Sie benötigen quadratische Terme im Modell, um die Krümmung über die gesamte Wirkungsfläche zu modellieren. Dies ist mit einem Wirkungsflächenversuchsplan möglich. Sie können den faktoriellen Versuchsplan mit Sternpunkten erweitern, um aus einem faktoriellen Versuchsplan einen zentral zusammengesetzten Wirkungsflächenversuchsplan zu erstellen.
Was sind vollfaktorielle und teilfaktorielle Versuchspläne?
Vollfaktorielle Versuchspläne
Ein vollfaktorieller Versuchsplan ist ein Versuchsplan, bei dem für sämtliche Kombinationen von Faktorstufen Messwerte für die Antwortvariable erfasst werden. Minitab bietet zwei Arten von vollfaktoriellen Versuchsplänen:
- Zweistufige vollfaktorielle Versuchspläne, die nur Faktoren mit 2 Stufen enthalten
- Allgemeine vollfaktorielle Versuchspläne, die Faktoren mit mehr als zwei Stufen enthalten
Für einen zweistufigen vollfaktoriellen Versuchsplan sind 2k Durchläufe erforderlich, wobei k für die Anzahl der Faktoren steht. Mit zunehmender Anzahl der Faktoren in einem zweistufigen faktoriellen Versuchsplan steigt die erforderliche Anzahl der Durchläufe zum Ausführen eines vollfaktoriellen Versuchsplans rapide an. Beispielsweise sind für einen zweistufigen vollfaktoriellen Versuchsplan mit sechs Faktoren 64 Durchläufe erforderlich, und für einen Versuchsplan mit neun Faktoren sind es bereits 512. Bei einem Versuchsplan mit 1/2-Fraktion wäre hingegen nur die Hälfte dieser Durchläufe erforderlich.
Teilfaktorielle Versuchspläne
Ein teilfaktorieller Versuchsplan ist ein Versuchsplan, bei dem nur eine ausgewählte Teilmenge oder „Fraktion“ der Durchläufe des vollfaktoriellen Versuchsplans ausgeführt wird. Teilfaktorielle Versuchspläne eignen sich gut für Situationen mit begrenzten Ressourcen oder für Versuchspläne mit einer hohen Anzahl von Faktoren, da weniger Durchläufe als bei einem vollfaktoriellen Versuchsplan anfallen.
In einem teilfaktoriellen Versuchsplan wird eine Teilmenge des vollfaktoriellen Versuchsplans analysiert, so dass einige Haupteffekte und Zwei-Faktor-Wechselwirkungen vermengt sind und nicht von den Effekten anderer Wechselwirkungen höherer Ordnung getrennt werden können. In der Regel sind die Versuchsleiter bereit, die Effekte höherer Ordnung als vernachlässigbar zu betrachten, um im Gegenzug mit einer geringeren Anzahl von Durchläufen Informationen zu Haupteffekten und Wechselwirkungen niedrigerer Ordnung zu gewinnen.
Was ist ein zweistufiger vollfaktorieller Versuchsplan?
In einem zweistufigen vollfaktoriellen Versuchsplan weisen die einzelnen experimentellen Faktoren nur zwei Stufen auf. Die experimentellen Durchläufe umfassen sämtliche Kombinationen dieser Faktorstufen. Obwohl mit zweistufigen faktoriellen Versuchsplänen weite Bereiche des Faktorraums nicht vollständig untersucht werden können, liefern sie mit relativ wenigen Durchläufen pro Faktor dennoch nützliche Informationen. Da zweistufige faktorielle Versuchspläne bedeutsame Trends aufdecken können, können Sie damit die Richtung für weitere Experimente ermitteln. Wenn beispielsweise ein Bereich untersucht werden soll, in dem die optimalen Einstellungen vermutet werden, kann der faktorielle Versuchsplan so erweitert werden, dass sich ein zentral zusammengesetzter Versuchsplan ergibt.
Vergleich
In den folgenden Diagrammen werden ein vollfaktorieller Versuchsplan und ein teilfaktorieller Versuchsplan mit ½-Fraktion gegenübergestellt.
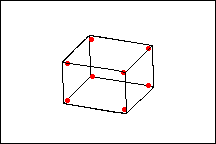
Vollfaktorieller Versuchsplan
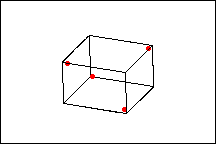
Teilfaktorieller Versuchsplan mit ½-Fraktion
Der vollfaktorielle Versuchsplan enthält doppelt so viele Versuchsplanpunkte wie der Versuchsplan mit ½-Fraktion. Die Antwortvariable wird nur für vier der acht möglichen Eckpunkte des faktoriellen Teils des Versuchsplans erfasst. Bei diesem Versuchsplan sind die Haupteffekte jedoch mit den Zwei-Faktor-Wechselwirkungen vermengt.
So ordnet Minitab die Fraktionen eines Versuchsplans an
| Fraktion | Standardreihenfolge (Yates-Reihenfolge) | Versuchsplangenerator |
|---|---|---|
| 1 | – – – | D = –AB, E = –AC, F = –BC |
| 2 | + – – | D = +AB, E = –AC, F = –BC |
| 3 | – + – | D = –AB, E = +AC, F = –BC |
| 4 | + + – | D = +AB, E = +AC, F = –BC |
| 5 | – – + | D = –AB, E = –AC, F = +BC |
| 6 | + – + | D = +AB, E = –AC, F = +BC |
| 7 | – + + | D = –AB, E = +AC, F = +BC |
| 8 | + + + | D = +AB, E = +AC, F = +BC |
Die Hauptfraktion ist stets die letzte Fraktion und weist nur positive Vorzeichen auf.
| Durchlauf | A | B | C | D = AB | E = –AC | F = –BC |
|---|---|---|---|---|---|---|
| 1 | – | – | – | + | – | – |
| 2 | + | – | – | – | + | – |
| 3 | – | + | – | – | – | + |
| 4 | + | + | – | + | + | + |
| 5 | – | – | + | + | + | + |
| 6 | + | – | + | – | – | + |
| 7 | – | + | + | – | + | – |
| 8 | + | + | + | + | – | – |
Auswählen einer anderen Fraktion als die Standardfraktion
Beim Erstellen eines teilfaktoriellen Versuchsplans verwendet Minitab in der Standardeinstellung die Hauptfraktion. In der Hauptfraktion sind alle Vorzeichen positiv. In bestimmten Situationen kann ein Versuchsplan jedoch Punkte enthalten, mit denen ein Durchlauf unpraktisch ist. Durch das Auswählen einer geeigneten Fraktion können diese Punkte vermieden werden.
- D = –AB E = –AC
- D = AB E = –AC
- D = –AB E = AC
- D = AB E = AC
Angenommen, der Versuchsplan konnte nicht mit allen fünf Faktoren auf der hohen Stufe ausgeführt werden. Die Hauptfraktion enthält zwar diesen Punkt, nicht aber die dritte Fraktion.
