Methode für Antworttabellen
Minitab berechnet eine Antworttabelle für jedes Merkmal der Antwortvariablen (d. h. Mittelwert, Signal-Rausch-Verhältnis, Standardabweichung). Anhand von Antworttabellen kann ersichtlich werden, welcher Faktor die größte Auswirkung auf die Antwortvariable hat und welche Stufe des Faktors mit höheren oder niedrigeren Werten für ein Merkmal der Antwortvariablen verbunden ist.
- Das ausgewählte Merkmal der Antwortvariablen wird für jede Kombination der Faktorstufen berechnet.
- Für jeden Faktor berechnet Minitab das durchschnittliche Merkmal der Antwortvariablen auf jeder Stufe des Faktors. Angenommen, Sie haben S/N-Verhältnisse ausgewählt, und der Versuchsplan enthält Faktor A, der zwei Stufen (1 und 2) und vier Messwerte pro Stufe aufweist. Minitab berechnet den Mittelwert der vier S/N-Verhältnisse auf Stufe 1 und den Mittelwert der anderen vier S/N-Verhältnisse auf Stufe 2.
- Minitab berechnet für jeden Faktor den Delta-Wert, d. h. den höchsten Durchschnittswert des Merkmals der Antwortvariablen minus den niedrigsten Durchschnittswert des Merkmals der Antwortvariablen für die Stufen des betreffenden Faktors.
- Der Rang wird berechnet, d. h. die Ordnung der Delta-Werte in absteigender Reihenfolge. Der Faktor mit dem höchsten Delta-Wert erhält Rang 1, der Faktor mit dem zweithöchsten Delta-Wert erhält Rang 2 usw.
Signal-Rausch-Verhältnis für statische Versuchspläne
Das Signal-Rausch-Verhältnis ist ein Maß für die Robustheit, mit dem die Einstellungen der Steuerfaktoren ermittelt werden können, bei denen der Effekt des Rauschens auf die Antwortvariable minimiert wird. Minitab berechnet für jede Kombination von Stufen der Steuerfaktoren im Versuchsplan ein eigenes Signal-Rausch-Verhältnis (S/N). Je nach Zielsetzung des Experiments können verschiedene S/N-Verhältnisse ausgewählt werden. In allen Fällen soll das S/N-Verhältnis maximiert werden.
Für statische Versuchspläne stellt Minitab vier S/N-Verhältnisse bereit: „Kleiner ist besser“, „Größer ist besser“ und zwei Verhältnisse vom Typ „Nominal ist am besten“. Darüber hinaus kann eine korrigierte Fassung der Formel „Nominal ist am besten (II)“ ausgewählt werden.
Größer ist besser
Das Signal-Rausch-Verhältnis (S/N) wird für jede Kombination von Faktorstufen berechnet. Die Formel für das S/N-Verhältnis „Größer ist besser“ unter Verwendung des Logarithmus zur Basis 10 lautet wie folgt:
S/N = −10*log(Σ(1/Y2)/n)
Hierbei ist Y = Werte der Antwortvariablen für die angegebene Kombination von Faktorstufen und n = Anzahl der Werte der Antwortvariablen für die Kombination von Faktorstufen.
Kleiner ist besser
Das Signal-Rausch-Verhältnis (S/N) wird für jede Kombination von Faktorstufen berechnet. Die Formel für das S/N-Verhältnis „Kleiner ist besser“ unter Verwendung des Logarithmus zur Basis 10 lautet wie folgt:
S/N = −10*log(Σ(Y2)/n)
Hierbei ist Y = Werte der Antwortvariablen für die angegebene Kombination von Faktorstufen und n = Anzahl der Werte der Antwortvariablen für die Kombination von Faktorstufen.
Nominal ist am besten (I)
Das Signal-Rausch-Verhältnis (S/N) wird für jede Kombination von Faktorstufen berechnet. Die Formel für das S/N-Verhältnis „Nominal ist am besten (I)“ unter Verwendung des Logarithmus zur Basis 10 lautet wie folgt:
S/N = −10*log(s2)
Hierbei ist s = Standardabweichung der Antwortvariablen für alle Rauschfaktoren für die angegebene Kombination von Faktorstufen.
Nominal ist am besten (II)
Das Signal-Rausch-Verhältnis (S/N) wird für jede Kombination von Faktorstufen berechnet. Die Formel für das S/N-Verhältnis „Nominal ist am besten (II)“ unter Verwendung des Logarithmus zur Basis 10 lautet wie folgt:
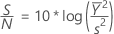
Darüber hinaus kann eine korrigierte Fassung der Formel „Nominal ist am besten“ für das S/N-Verhältnis ausgewählt werden. Die Formel lautet wie folgt:
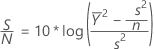
Dabei gilt Folgendes:



Signal-Rausch-Verhältnis für dynamische Versuchspläne
Das Signal-Rausch-Verhältnis ist ein Maß für die Robustheit, mit dem die Einstellungen der Steuerfaktoren ermittelt werden können, bei denen der Effekt des Rauschens auf die Antwortvariable minimiert wird. Minitab berechnet für jede Kombination von Stufen der Steuerfaktoren im Versuchsplan ein eigenes Signal-Rausch-Verhältnis (S/N). Je nach Zielsetzung des Experiments können verschiedene S/N-Verhältnisse ausgewählt werden. In allen Fällen soll das S/N-Verhältnis maximiert werden.
Für dynamische Versuchspläne ähnelt das S/N-Verhältnis stark dem S/N-Verhältnis „Nominal ist am besten“.
Formel
Die Formel für das Signal-Rausch-Verhältnis (S/N) für einen dynamischen Taguchi-Versuchsplan unter Verwendung des Logarithmus zur Basis 10 lautet wie folgt:
S/N = 10*log [(Steigung)2 / MSE]
Hierbei ist MSE = mittleres Fehlerquadrat.
Darüber hinaus kann die korrigierte Fassung der Formel für das dynamische Signal-Rausch-Verhältnis ausgewählt werden:
S/N = 10*log [(Steigung2 / MSE) – (1/r)]
Hierbei ist r = Σ(Signal – Ref)2 und Ref = Referenzsignal (sofern vorhanden) oder mittleres Signal.
