Beispiel für Taguchi-Versuchsplan analysieren (statisch)

Ein Techniker bei einem Hersteller von Golfausrüstungen möchte einen neuen Golfball mit längerer Flugweite entwickeln. Der Techniker hat vier Steuerfaktoren (Kernmaterial, Kerndurchmesser, Anzahl der Dimples und Außenhautstärke) sowie einen Rauschfaktor (Typ des Golfschlägers) ermittelt. Jeder Steuerfaktor weist zwei Stufen auf. Der Rauschfaktor ergibt sich durch zwei Typen von Golfschlägern: Driver und Eisen 5. Der Techniker misst die Flugweite für jeden Typ von Golfschläger und erfasst die Daten in zwei Rauschfaktorspalten im Arbeitsblatt.

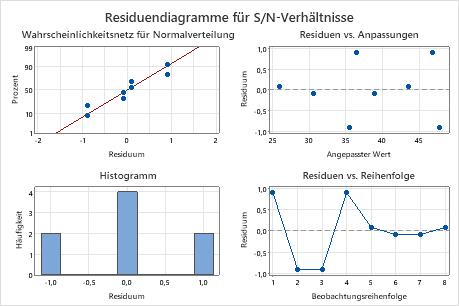
Da das Ziel des Experiments darin besteht, die Flugweite zu maximieren, verwendet der Techniker das Signal-Rausch-Verhältnis (S/N) „Größer ist besser“. Er möchte außerdem die Wechselwirkung zwischen dem Kernmaterial und dem Kerndurchmesser untersuchen.

Öffnen Sie die Beispieldaten Golfball.MTW.
Wählen Sie Statistik > Versuchsplanung (DOE) > Taguchi > Taguchi-Versuchsplan analysieren aus.
Geben Sie im Feld Antwortdaten befinden sich in die Spalten Driver und Eisen ein.
Klicken Sie auf Analyse.
Aktivieren Sie unter Lineares Modell anpassen für die Optionen Signal-Rausch-Verhältnisse und Mittelwerte. Klicken Sie auf OK.
Klicken Sie auf Terme.
Verschieben Sie die Terme A: Material, B: Durchmesser, C: Dimples, D: Stärke und AB aus Verfügbare Terme nach Ausgewählte Terme. Klicken Sie auf OK.
Klicken Sie auf Optionen.
Wählen Sie unter Signal-Rausch-Verhältnis die Option Größer ist besser aus. Klicken Sie auf OK.
Klicken Sie auf Analysegrafiken, und wählen Sie dann Vier-in-eins aus.
Klicken Sie in den einzelnen Dialogfeldern auf OK.

Interpretieren der Ergebnisse

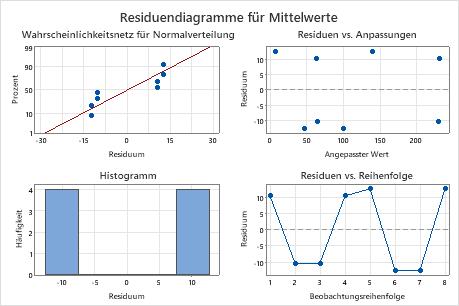
Minitab gibt eine Tabelle der geschätzten Regressionskoeffizienten für jedes ausgewählte Merkmal der Antwortvariablen aus. In diesem Beispiel wählt der Techniker zwei Merkmale der Antwortvariablen aus: das Signal-Rausch-Verhältnis (S/N) und die Mittelwerte. Verwenden Sie die p-Werte, um zu ermitteln, welche Faktoren statistisch signifikant sind, und verwenden Sie die Koeffizienten, um die relative Bedeutung jedes Faktors im Modell zu bestimmen.

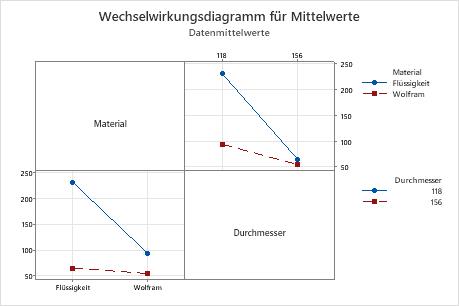
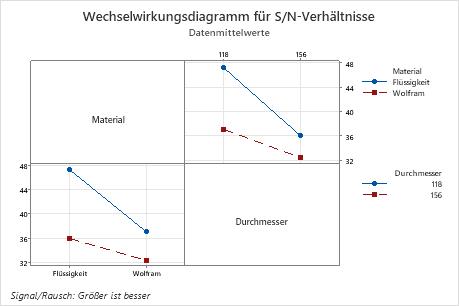
In diesem Beispiel weisen alle Faktoren für die S/N-Verhältnisse einen kleineren p-Wert als 0,05 auf, und sie sind bei einem Signifikanzniveau von 0,05 statistisch signifikant. Häufig wird ein Signifikanzniveau von 0,10 für die Auswertung von Termen in einem Modell verwendet. Die Wechselwirkung ist auf dem Signifikanzniveau 0,10 statistisch signifikant. Für die Mittelwerte sind das Kernmaterial (p = 0,045) und der Kerndurchmesser (p = 0,024) auf dem Signifikanzniveau 0,05 statistisch signifikant, und die Wechselwirkung zwischen Material und Durchmesser (p = 0,06) ist auf dem Signifikanzniveau 0,10 statistisch signifikant. Da jedoch beide Faktoren an der Wechselwirkung beteiligt sind, müssen Sie zunächst die Wechselwirkung genauer untersuchen, bevor Sie den Effekt jedes Faktors einzeln betrachten können.

Der Absolutwert des Koeffizienten gibt die relative Bedeutung jedes Faktors an. Der Faktor mit dem größten Koeffizienten hat die größte Auswirkung auf ein bestimmtes Merkmal der Antwortvariablen. In Taguchi-Versuchsplänen spiegelt die Größe des Faktorkoeffizienten in der Regel die Rangfolge der Faktoren in den Antworttabellen wider.

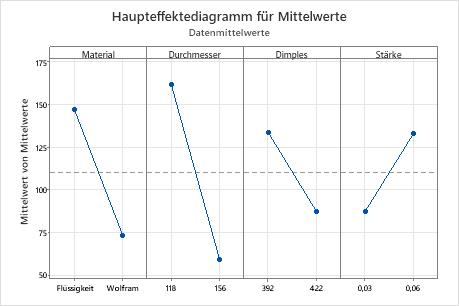
Die Antworttabellen zeigen für jede Stufe jedes Faktors den Durchschnitt für jede Eigenschaft der Antwortvariablen. Die Tabelle umfasst Ränge auf der Grundlage der Delta-Statistik, mit der die relativen Größen von Effekten verglichen werden. In der Delta-Statistik wird für jeden Faktor der kleinste Durchschnitt vom größten abgezogen. Minitab weist die Ränge auf der Grundlage von Delta-Werten zu; Rang 1 dem höchsten Delta-Wert, Rang 2 dem zweithöchsten usw. Ermitteln Sie mit Hilfe der Stufendurchschnitte in den Antworttabellen, welche Stufe jedes Faktors das beste Ergebnis liefert.

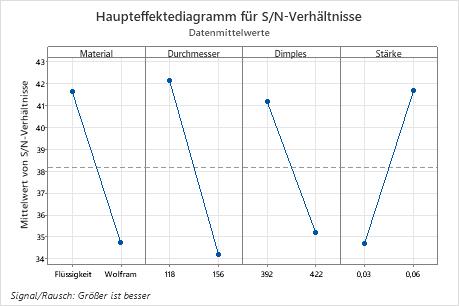
In Taguchi-Experimenten soll stets das S/N-Verhältnis maximiert werden. In diesem Beispiel deuten die Ränge darauf hin, dass der Kerndurchmesser (B) den größten Einfluss auf das S/N-Verhältnis und den Mittelwert ausübt. In Bezug auf das S/N-Verhältnis weist die Außenhautstärke (D) den nächstgrößten Einfluss auf, dann folgen das Kernmaterial (A) und die Anzahl der Dimples (C). In Bezug auf die Mittelwerte weist das Kernmaterial (A) den nächstgrößten Einfluss auf, dann folgen die Anzahl der Dimples (C) und die Außenhautstärke (D).

Da in diesem Beispiel das Ziel in der Verlängerung der Flugweite der Golfbälle besteht, ist der Techniker an den Faktorstufen interessiert, die zu dem größten Mittelwert führen. Die Mittelwerte in den Tabellen der Antwortvariablen zeigen, dass die S/N-Verhältnisse und die Mittelwerte bei einem Wert der Stufe 1 für jeden Faktor maximiert werden, mit Ausnahme der Deckungsdicke. Dies entspricht den folgenden Faktoreinstellungen:

Flüssiger Kern (A)
Kerndurchmesser (B) = 118
Anzahl Dimples (C) = 392
Außenhautstärke (D) = 0,06

Die Haupteffektediagramme und die Wechselwirkungsdiagramme bestätigen diese Ergebnisse. Die Wechselwirkungsdiagramme zeigen, dass die Flugweite bei einem flüssigen Kern maximiert wird, wenn der Kerndurchmesser 118 beträgt.

Um diese Analyse fortzusetzen, kann der Techniker mit Hilfe von Taguchi-Ergebnisse prognostizieren die prognostizierten S/N-Verhältnisse und Mittelwerte bei diesen Faktoreinstellungen bestimmen. Weitere Informationen finden Sie unter Beispiel für Taguchi-Ergebnisse prognostizieren.

Term	Koef	SE Koef	t	p
Konstante	38,181	0,4523	84,418	0,000
Material Flüssigk	3,436	0,4523	7,596	0,017
Durchmes 118	3,967	0,4523	8,772	0,013
Dimples 392	2,982	0,4523	6,593	0,022
Stärke 0,03	-3,479	0,4523	-7,692	0,016
Material*Durchmes Flüssigk 118	1,640	0,4523	3,625	0,068

Quelle	DF	Seq SS	Kor SS	Kor MS	F	p
Material	1	94,427	94,427	94,427	57,70	0,017
Durchmesser	1	125,917	125,917	125,917	76,94	0,013
Dimples	1	71,133	71,133	71,133	43,47	0,022
Stärke	1	96,828	96,828	96,828	59,17	0,016
Material*Durchmesser	1	21,504	21,504	21,504	13,14	0,068
Residuenfehler	2	3,273	3,273	1,637
Gesamt	7	413,083

Term	Koef	SE Koef	t	p
Konstante	110,40	8,098	13,634	0,005
Material Flüssigk	36,86	8,098	4,552	0,045
Durchmes 118	51,30	8,098	6,335	0,024
Dimples 392	23,25	8,098	2,871	0,103
Stärke 0,03	-22,84	8,098	-2,820	0,106
Material*Durchmes Flüssigk 118	31,61	8,098	3,904	0,060

Quelle	DF	Seq SS	Kor SS	Kor MS	F	p
Material	1	10871	10871	10870,8	20,72	0,045
Durchmesser	1	21054	21054	21053,5	40,13	0,024
Dimples	1	4325	4325	4324,5	8,24	0,103
Stärke	1	4172	4172	4172,4	7,95	0,106
Material*Durchmesser	1	7995	7995	7994,8	15,24	0,060
Residuenfehler	2	1049	1049	524,6
Gesamt	7	49465

Stufe	Material	Durchmesser	Dimples	Stärke
1	41,62	42,15	41,16	34,70
2	34,75	34,21	35,20	41,66
Delta	6,87	7,93	5,96	6,96
Rang	3	1	4	2

Beispiel für Taguchi-Versuchsplan analysieren (statisch)

Interpretieren der Ergebnisse

Geschätzte Modellkoeffizienten für S/N-Verhältnisse

Zusammenfassung des Modells

Varianzanalyse für S/N-Verhältnisse

Geschätzte Modellkoeffizienten für Mittelwerte

Zusammenfassung des Modells

Varianzanalyse für Mittelwerte

Antworttabelle für Signal-Rausch-Verhältnisse

Antworttabelle für Mittelwerte

Stufe	Material	Durchmesser	Dimples	Stärke
1	147,26	161,70	133,65	87,56
2	73,54	59,10	87,15	133,24
Delta	73,73	102,60	46,50	45,68
Rang	2	1	3	4