Versuchsplanmatrix
Zunächst erstellt Minitab auf der Grundlage der Faktoren und des angegebenen Modells eine Versuchsplanmatrix. Die Spalten dieser Matrix stellen die Terme im Modell dar. Anschließend fügt Minitab weitere Spalten für den den konstanten Term, Blöcke und Terme höherer Ordnung hinzu, um die Versuchsplanmatrix für das Modell in der Analyse fertigzustellen.
Versuchspläne, die ausschließlich stetige Faktoren enthalten
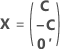
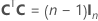
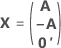
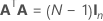
Die vollständige Versuchsplanmatrix enthält Spalten zusätzlich zu den Spalten, die Faktoren darstellen. Die Versuchsplanmatrix enthält eine Spalte von Einsen für den konstanten Term. Die vollständige Versuchsplanmatrix enthält zudem Spalten, die im Modell enthaltene quadratische Terme und Wechselwirkungsterme darstellen.
Versuchspläne mit kategorialen Faktoren
Für einen Versuchsplan mit kategorialen Faktoren ersetzt Minitab die Zeile mit dem einzelnen Zentralpunkt in der Versuchsplanmatrix durch zwei Pseudo-Zentralpunkte. Wenn der Versuchsplan lediglich einen kategorialen Faktor enthält, sind nur zwei mögliche Pseudo-Zentralpunkte vorhanden, so dass beide Punkte im Versuchsplan enthalten sind.
Wenn der Versuchsplan mehr als zwei kategoriale Faktoren enthält, wählt Minitab mit Hilfe eines iterativen Algorithmus zwei einzubindende Pseudo-Zentralpunkte aus. Der Algorithmus minimiert die Varianz der Regressionskoeffizienten für die linearen Effekte im Modell.
Notation
| Begriff | Beschreibung |
|---|---|
| C | Eine Conference-Matrix |
| 0' | Eine Zeile mit Nullen in einer Matrix, die einen Durchlauf mit dem Zentralpunkt darstellt |
| In | n × n-Identitätsmatrix |
| A | Eine Matrix, die eine Teilmenge einer Conference-Matrix mit N Zeilen und n Spalten darstellt, wobei Folgendes gilt:  |
| N | Anzahl der Zeilen in der Teilmenge der Spalten aus der Conference-Matrix |
| n | Anzahl der Faktoren in einem Versuchsplan |
Koeffizient (Koef)
Ausgedrückt unter Verwendung von Matrizen lautet die Formel zum Berechnen des Vektors von Koeffizienten im Modell wie folgt:

Notation
| Begriff | Beschreibung |
|---|---|
| X | Versuchsplanmatrix |
| Y | Vektor der Antwortvariablen |
Box-Cox-Transformation
Bei der Box-Cox-Transformation werden Lambda-Werte (siehe unten) ausgewählt, die die Summe der Quadrate der Residuen minimieren. Die resultierende Transformation ist Y λ, wenn λ ≠ 0, und ln(Y), wenn λ = 0. Wenn λ < 0, multipliziert Minitab zudem die transformierte Antwortvariable mit −1, um die Reihenfolge aus der nicht transformierten Antwortvariablen beizubehalten.
Minitab sucht einen optimalen Wert zwischen −2 und 2. Werte, die außerhalb dieses Intervalls liegen, führen möglicherweise nicht zu einer besseren Anpassung.
Hier finden Sie einige der gängigsten Transformationen, wobei Y′ das transformierte Y der Daten darstellt:
| Lambda-Wert (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 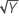 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Gewichtete Regression
Bei der Regression der gewichteten kleinsten Quadrate handelt es sich um eine Methode zum Behandeln von Beobachtungen, deren Varianzen nicht konstant sind. Wenn die Varianzen nicht konstant sind, gelten für die Beobachtungen folgende Hinweise:
- Großen Varianzen sollten relativ kleine Gewichtungen zugewiesen werden.
- Kleinen Varianzen sollten relativ große Gewichtungen zugewiesen werden.
Üblicherweise wird für die Gewichtungen die Umkehrung der reinen Fehlervarianz in der Antwortvariablen ausgewählt.
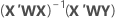
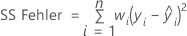
Notation
| Begriff | Beschreibung |
|---|---|
| X | Designmatrix |
| X' | transponierte Designmatrix |
| W | eine (n x n)-Matrix mit den Gewichtungen auf der Diagonalen |
| Y | Vektor von Werten der Antwortvariablen |
| n | Anzahl der Beobachtungen |
| wi | Gewichtung für die i-te Beobachtung |
| yi | Wert der Antwortvariablen für die i-te Beobachtung |
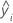 | angepasster Wert für die i-te Beobachtung |
