Methoden in Binäre Antwort für definitiven Screening-Versuchsplan analysieren

Die Erweiterung der klassischen linearen Modelle auf verallgemeinerte lineare Modelle umfasst zwei Teile: eine Verteilung aus der Exponentialfamilie und eine Linkfunktion.

Exponentialfamilie

Der erste Teil erweitert das lineare Modell auf Antwortvariablen, die zu einer großen Familie von Verteilungen gehören, die als Exponentialfamilie bezeichnet werden. Mitglieder der Exponentialfamilie von Verteilungen weisen Dichtefunktionen für einen beobachteten Wert der Antwortvariablen in dieser allgemeinen Form auf:

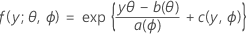
Hierbei gilt: a(∙), b(∙) und c(∙) hängen von der Verteilung der Antwortvariablen ab. Der Parameter θ ist ein Lageparameter, der oft als kanonischer Parameter bezeichnet wird, und ϕ wird als Streuungsparameter bezeichnet. Die Funktion a(ϕ) hat meistens die Form a(ϕ) = ϕ/ ω, wobei ω eine bekannte Konstante oder Gewichtung ist, die zwischen den Beobachtungen variieren kann. (Wenn in Minitab Gewichtungen angegeben werden, wird die Funktion a(ϕ) entsprechend korrigiert.)

Bei Mitgliedern der Exponentialfamilie kann es sich um diskrete Verteilungen oder stetige Verteilungen handeln. Beispiele für stetige Verteilungen, die zur Exponentialfamilie gehören, sind die Normalverteilung und die Gamma-Verteilung. Zu den diskreten Verteilungen, die zur Exponentialfamilie gehören, zählen zum Beispiel die Binomialverteilung und die Poisson-Verteilung. In der folgenden Tabelle werden die Merkmale einiger dieser Verteilungen aufgeführt.

Verteilung	ϕ	b(θ)	a(φ)	c(y, ϕ)
Normal	σ2	θ2/2	φω
Binomial	1		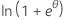φ/ω	-ln(y!)
Poisson	1	exp(θ)	φ/ω

Linkfunktion

Der zweite Teil ist die Linkfunktion. Die Linkfunktion setzt den Mittelwert der Antwortvariablen in der i-ten Beobachtung in folgender Form zu einem linearen Prädiktor in Beziehung:

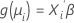
Das klassische lineare Modell ist ein Sonderfall dieser allgemeinen Formel, wobei die Linkfunktion die Identitätsfunktion ist.

Die Auswahl der Linkfunktion im zweiten Teil hängt von der spezifischen Verteilung der Exponentialfamilie im ersten Teil ab. Jede Verteilung in der Exponentialfamilie weist eine bestimmte Linkfunktion auf, die als kanonische Linkfunktion bezeichnet wird. Diese Linkfunktion erfüllt die Gleichung g (μ_i) = X_i'β = θ, wobei θ der kanonische Parameter ist. Die kanonische Linkfunktion ergibt einige erwünschte statistische Eigenschaften des Modells. Mit Hilfe der Statistiken für die Güte der Anpassung können Sie die Anpassungen mit den verschiedenen Linkfunktionen vergleichen. Bestimmte Linkfunktionen können aus historischen Gründen verwendet werden, oder weil sie eine bestimmte Bedeutung in einer Disziplin haben. Beispielsweise besteht ein Vorteil der Logit-Linkfunktion darin, dass sie einen Schätzwert für das Chancenverhältnis liefert. Ein weiteres Beispiel ist die Normit-Linkfunktion: Bei dieser wird angenommen, dass eine zugrunde liegende Variable vorhanden ist, die einer Normalverteilung folgt und in binäre Kategorien unterteilt ist.

Minitab bietet drei Linkfunktionen. Mit Hilfe der verschiedenen Linkfunktionen können Sie Modelle bestimmen, die bei unterschiedlich ausgeprägten Daten eine adäquate Anpassung bieten. Die folgenden Linkfunktionen sind verfügbar: Logit, Normit (auch als Probit bezeichnet) und Gompit (auch als komplementärer Log-Log bezeichnet). Hierbei handelt es sich um die Umkehrung der regulären kumulativen logistischen Verteilungsfunktion (Logit), die Umkehrung der regulären kumulativen Normalverteilungsfunktion (Normit) und die Umkehrung der Gompertz-Verteilungsfunktion (Gompit). Die Logit-Linkfunktion ist die kanonische Linkfunktion für Binomialmodelle, und somit ist Logit die standardmäßig vorgegebene Linkfunktion.

Modell	Name	Linkfunktion, g(μi)
Binomial	Logit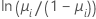
Binomial	Normit (Probit)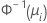
Binomial	Gompit (komplementärer Log-Log)

Notation

Begriff	Beschreibung
μi	Mittelwert der Antwortvariablen in der i-ten Zeile
g(μi)	Linkfunktion
X	Vektor der Prädiktorvariablen
β	Vektor der Koeffizienten, die den Prädiktoren zugeordnet sind
	inverse kumulative Verteilungsfunktion der Normalverteilung

Beschreibt einen einzelnen Satz von Faktoren-/Kovariatenwerten in einem Datensatz. Minitab berechnet für jedes Faktoren-/Kovariatenmuster Ereigniswahrscheinlichkeiten, Residuen und weitere Bewertungsmaße.

Wenn ein Datensatz beispielsweise die Faktoren Geschlecht und Ethnie sowie die Kovariate Alter enthält, können die Kombinationen dieser Prädiktoren so viele verschiedene Kovariatenmuster wie Probanden enthalten. Wenn ein Datensatz nur die Faktoren Ethnie und Geschlecht enthält, die jeweils auf zwei Stufen kodiert sind, gibt es nur vier mögliche Faktoren-/Kovariatenmuster. Wenn Sie die Daten als Häufigkeiten oder als Erfolge, Versuche oder Misserfolge eingeben, enthält jede Zeile ein Faktoren-/Kovariatenmuster.

Zunächst erstellt Minitab auf der Grundlage der Faktoren und des angegebenen Modells eine Versuchsplanmatrix. Die Spalten dieser Matrix stellen die Terme im Modell dar. Anschließend fügt Minitab weitere Spalten für den den konstanten Term, Blöcke und Terme höherer Ordnung hinzu, um die Versuchsplanmatrix für das Modell in der Analyse fertigzustellen.

Versuchspläne, die ausschließlich stetige Faktoren enthalten

Die Form der Versuchsplanmatrix hängt davon ab, ob eine Conference-Matrix mit der gleichen Anzahl von Zeilen wie Faktoren vorhanden ist. Wenn dieses Kriterium erfüllt ist, weisen die Spalten der Versuchsplanmatrix, die die Faktoren darstellen, die folgende Form auf:

Hierbei ist C eine n × n-Conference-Matrix mit den Elementen {–1, 0, 1}, die dieser Eigenschaft entspricht:

Wenn keine Conference-Matrix der richtigen Größe vorhanden ist, sind die Spalten, die die Faktoren darstellen, eine Teilmenge einer umfassenderen Conference-Matrix:

Hierbei ist A eine N × n-Matrix mit den Elementen {–1, 0, 1}, die dieser Eigenschaft entspricht:

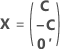
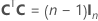
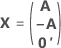
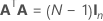
Die vollständige Versuchsplanmatrix enthält Spalten zusätzlich zu den Spalten, die Faktoren darstellen. Die Versuchsplanmatrix enthält eine Spalte von Einsen für den konstanten Term. Die vollständige Versuchsplanmatrix enthält zudem Spalten, die im Modell enthaltene quadratische Terme und Wechselwirkungsterme darstellen.

Versuchspläne mit kategorialen Faktoren

Für einen Versuchsplan mit kategorialen Faktoren ersetzt Minitab die Zeile mit dem einzelnen Zentralpunkt in der Versuchsplanmatrix durch zwei Pseudo-Zentralpunkte. Wenn der Versuchsplan lediglich einen kategorialen Faktor enthält, sind nur zwei mögliche Pseudo-Zentralpunkte vorhanden, so dass beide Punkte im Versuchsplan enthalten sind.

Wenn der Versuchsplan mehr als zwei kategoriale Faktoren enthält, wählt Minitab mit Hilfe eines iterativen Algorithmus zwei einzubindende Pseudo-Zentralpunkte aus. Der Algorithmus minimiert die Varianz der Regressionskoeffizienten für die linearen Effekte im Modell.

Notation

Begriff	Beschreibung
C	Eine Conference-Matrix
0'	Eine Zeile mit Nullen in einer Matrix, die einen Durchlauf mit dem Zentralpunkt darstellt
In	n × n-Identitätsmatrix
A	Eine Matrix, die eine Teilmenge einer Conference-Matrix mit N Zeilen und n Spalten darstellt, wobei Folgendes gilt:
N	Anzahl der Zeilen in der Teilmenge der Spalten aus der Conference-Matrix
n	Anzahl der Faktoren in einem Versuchsplan