In diesem Thema
Angepasste und prognostizierte Werte
Zum Berechnen der Prognose kehren Sie die Linkfunktion für das Modell um. Die Umkehrfunktionen finden Sie in der folgenden Tabelle.
| Linkfunktion | Formel für die Prognose |
|---|---|
| Logit | 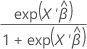 |
| Normit | 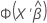 |
| Gompit |  |
Notation
| Begriff | Beschreibung |
|---|---|
| exp(·) | Exponentialfunktion |
| Φ(·) | kumulative Verteilungsfunktion der Normalverteilung |
| X' | transponierter Vektor der Punkte, für die Prognosen vorgenommen werden sollen |
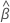 | Vektor der geschätzten Koeffizienten |
Standardfehler der angepassten Werte und Prognosen
Im Allgemeinen hat der Standardfehler der Anpassung die folgende Form:
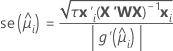
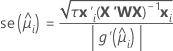
Die folgenden Formeln geben den Standardfehler der Passung für verschiedene Linkfunktionen an:
- Logit
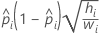
- Normit
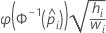
- Gompit

Beachten Sie die folgende Beziehung, die für die Formeln in der Tabelle gilt: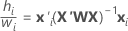
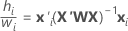
Hierbei ist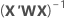 aus den Trainingsdaten nur, wenn ein Testdatensatz für die Validierung vorhanden ist.
aus den Trainingsdaten nur, wenn ein Testdatensatz für die Validierung vorhanden ist.
Notation
| Begriff | Beschreibung |
|---|---|
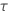 | 1, for the binomial and Poisson models |
| xi | the vector of a design point |
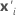 | the transpose of xi |
| X | the design matrix |
| W | the weight matrix |
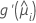 | the first derivative of the link function evaluated at 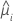 |
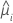 | the predicted mean response |
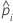 | the predicted probability for the design point in a binary logistic model |
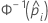 | the inverse cumulative distribution function of the standard normal distribution for the predicted probability in a binary logistic model |
 | the probability density function of the standard normal distribution |
Konfidenzgrenzen für Anpassungen und Prognosen
Für die Konfidenzgrenzen wird die Approximationsmethode nach Wald verwendet. Die Formel für ein beidseitiges 100(1 – α)%-Konfidenzintervall lautet:
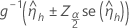
Notation
| Begriff | Beschreibung |
|---|---|
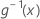 | Umkehrung der Linkfunktion, ausgewertet bei x |
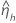 | 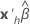 |
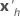 | transponierter Vektor der Prädiktoren |
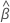 | Vektor der geschätzten Koeffizienten |
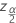 | Wert der inversen kumulativen Verteilungsfunktion der Normalverteilung, ausgewertet bei  |
| α | Signifikanzniveau |
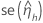 |  |
| X | Versuchsplanmatrix |
| W | Gewichtungsmatrix |
 | 1, für Binomialmodelle |
