Methoden und Formeln für die Varianzanalyse in Binäre Antwort für definitiven Screening-Versuchsplan analysieren

In diesem Thema

Varianzanalyse
Freiheitsgrade (DF)
Log-Likelihood
p-Wert (p)

Varianzanalyse

Die Abweichung ist ein Maß für die Unterschiede zwischen dem aktuellen Modell und dem vollständigen Modell. Bei dem vollständigen Modell handelt es sich um ein Modell mit n Parametern, einen Parameter pro Beobachtung. Das vollständige Modell maximiert die Log-Likelihood-Funktion. Es liefert einen Anhaltspunkt für Vergleiche von Modellen mit weniger als n Parametern. Bei Vergleichen mit dem vollständigen Modell wird die skalierte Abweichung verwendet.

Die folgende Gleichung gibt den Beitrag zur skalierten Abweichung für ein Modell mit Binomialverteilung an:

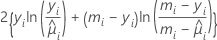
Die Abweichungstabelle wird auf der Grundlage des folgenden allgemeinen Ergebnisses erstellt, bei dem angenommen wird, dass ϕ bekannt ist. Wenn D_I die einem Anfangsmodell zugeordnete Abweichung und D_S die einer Teilmenge von Termen im Anfangsmodell zugeordnete Abweichung ist, liegt unter einigen Regularitätsbedingungen die folgende Beziehung vor:

Die Differenz zwischen den Abweichungen ist asymptotisch als Chi-Quadrat-Verteilung mit d Freiheitsgraden verteilt. Diese Statistiken werden für die korrigierte Analyse (Typ III) und die sequenzielle Analyse (Typ I) berechnet. Die korrigierte Abweichung und die Chi-Quadrat-Statistik in der Abweichungstabelle sind gleich. Die korrigierte mittlere Abweichung ist die korrigierte Abweichung dividiert durch die Freiheitsgrade.

Bei der sequenziellen Analyse hängt das Ergebnis von der Reihenfolge ab, in der die Prädiktoren in das Modell eingegeben werden. Die sequenzielle Abweichung ist der eindeutige Teil der Abweichung, der durch einen Prädiktor erklärt wird, wenn bereits Prädiktoren im Modell vorhanden sind. Bei einem Modell mit den drei Prädiktoren X1, X2 und X3 zeigt die sequenzielle Abweichung für X3, wie viel der verbleibenden Abweichung durch X3 erklärt wird, wenn X1 und X2 bereits im Modell enthalten sind. Um eine andere sequenzielle Abweichung zu erhalten, wiederholen Sie das Regressionsverfahren, und geben Sie die Prädiktoren in einer anderen Reihenfolge ein.

Wenn ϕ unbekannt ist, zum Beispiel bei Antwortvariablen, die einer Normalverteilung folgen, ändert sich die Beziehung unter einigen Regularitätsbedingungen wie folgt:

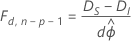
Hier ist die Differenz zwischen den Abweichungen asymptotisch als F-Verteilung mit d Freiheitsgraden für den Zähler und n − p Freiheitsgraden für den Nenner verteilt. Um den Streuungsparameter zu schätzen, verwenden Sie das Anfangsmodell.

Notation

Begriff	Beschreibung
y_i	Anzahl der Ereignisse für die i-te Zeile
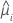	geschätzter Mittelwert der Antwortvariablen für die i-te Zeile
m_i	Anzahl der Versuche für die i-te Zeile
L_f	Log-Likelihood des vollständigen Modells
L_c	Log-Likelihood des Modells mit einer Teilmenge von Termen aus dem vollständigen Modell
d	Freiheitsgrade; die Differenz zwischen der Anzahl der Parameter in den zu vergleichenden Modellen
ϕ	Streuungsparameter, der für das Modell mit Binomialverteilung als 1 bekannt ist
n	Anzahl der Zeilen in den Daten
p	Freiheitsgrade der Regression für das Anfangsmodell

Freiheitsgrade (DF)

Unterschiedliche Summen der Quadrate weisen unterschiedliche Freiheitsgrade auf.

DF für einen numerischen Faktor = 1

DF für einen kategorialen Faktor = b − 1

DF für einen quadratischen Term = 1

DF für Blöcke = c − 1

DF für Fehler = n − p

DF Gesamt = n − 1

Für Wechselwirkungen zwischen Faktoren multiplizieren Sie die Freiheitsgrade für die Terme im Faktor. Wenn beispielsweise die Faktoren A und B gegeben sind, weist die Wechselwirkung AB diese Freiheitsgrade auf:

Um die Freiheitsgrade für einen Typ von Term zu ermitteln, summieren Sie die Freiheitsgrade für die Terme. Wenn beispielsweise die Faktoren A und B gegeben sind, weisen die Haupteffekte im Modell die folgende Anzahl von Freiheitsgraden auf:

Hinweis

Kategoriale Faktoren in Screening-Versuchsplänen von Minitab weisen zwei Stufen auf. Daher belaufen sich die Freiheitsgrade für einen kategorialen Faktor auf 2 – 1 = 1. Folglich weisen Wechselwirkungen zwischen Faktoren ebenfalls 1 Freiheitsgrad auf.

Notation

Begriff	Beschreibung
b	Anzahl der Stufen im Faktor
c	Anzahl der Blöcke
n	Gesamtzahl der Zeilen im Versuchsplan
n_i	Anzahl der Beobachtungen für die i-te Faktorstufenkombination
m	Anzahl der Faktorstufenkombinationen
p	Anzahl der Koeffizienten

Log-Likelihood

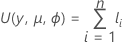
Die Log-Likelihood-Funktionen sind in Bezug auf die Mittelwerte parametrisiert. Die allgemeine Form der Funktionen lautet:

Die allgemeine Form der einzelnen Beiträge lautet:

Die folgende Gleichung gibt die spezifische Form der individuellen Beiträge für das Modell mit Binomialverteilung an:

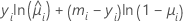
Notation

Begriff	Beschreibung
y_i	Anzahl der Ereignisse für die i-te Zeile
m_i	Anzahl der Versuche für die i-te Zeile
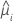	geschätzter Mittelwert der Antwortvariablen für die i-te Zeile

p-Wert (p)

p-Werte werden in Hypothesentests verwendet, um Ihnen die Entscheidung zu ermöglichen, ob eine Nullhypothese zurückgewiesen oder nicht zurückgewiesen werden sollte. Der p-Wert stellt die Wahrscheinlichkeit dar, eine Teststatistik zu erhalten, die mindestens so extrem wie der tatsächlich berechnete Wert ist, wenn die Nullhypothese wahr ist. Ein häufig verwendeter Trennwert für den p-Wert ist 0,05. Wenn beispielsweise der berechnete p-Wert einer Teststatistik kleiner als 0,05 ist, weisen Sie die Nullhypothese zurück.