In diesem Thema
- Schritt 1: Ermitteln, welche Terme den größten Effekt auf die Antwortvariable haben
- Schritt 2: Bestimmen, welche Terme statistisch signifikante Effekte auf die Antwortvariable haben
- Schritt 3: Verstehen der Effekte der Prädiktoren
- Schritt 4: Bestimmen, wie gut das Modell an die Daten angepasst ist
- Schritt 5: Bestimmen, ob das Modell nicht an Ihre Daten angepasst ist
Schritt 1: Ermitteln, welche Terme den größten Effekt auf die Antwortvariable haben
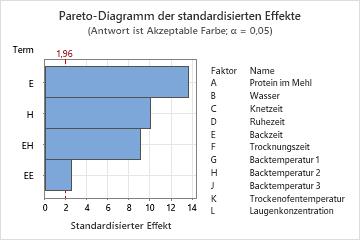
Verwenden Sie ein Pareto-Diagramm der standardisierten Effekte, um die relative Größe und die statistische Signifikanz von Haupteffekten, quadratischen Effekten und Wechselwirkungseffekten zu vergleichen.
Minitab stellt die standardisierten Effekte in absteigender Reihenfolge ihrer Absolutwerte dar. Die Referenzlinie im Diagramm zeigt, welche Effekte signifikant sind. In der Standardeinstellung zeichnet Minitab die Referenzlinie bei einem Signifikanzniveau von 0,05.
Wichtigste Ergebnisse: Pareto-Diagramm
In diesen Ergebnissen enthält das Diagramm nur Terme, die sich im Modell befinden. Im Diagramm wird ersichtlich, dass zwei Haupteffekte statistisch signifikant sind. Ein quadratischer Term und ein Wechselwirkungseffekt sind ebenfalls statistisch signifikant.
Darüber hinaus können Sie feststellen, dass E der größte Effekt ist, da der entsprechende Balken am längsten ist. Der Effekt für den quadratischen Term EE ist am kleinsten, da der entsprechende Balken am kürzesten ist.
Schritt 2: Bestimmen, welche Terme statistisch signifikante Effekte auf die Antwortvariable haben
- p-Wert ≤ α: Die Assoziation ist statistisch signifikant
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht.
- p-Wert > α: Die Assoziation ist statistisch nicht signifikant
- Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht. Es empfiehlt sich möglicherweise, das Modell ohne den Term erneut anzupassen.
- Faktoren
- Wenn ein Koeffizient für einen Faktor signifikant ist, können Sie schlussfolgern, dass die Wahrscheinlichkeit des Ereignisses nicht für alle Stufen des Faktors gleich ist.
- Wechselwirkungen zwischen Faktoren
- Wenn ein Koeffizient für einen Wechselwirkungsterm signifikant ist, hängt die Beziehung zwischen einem Faktor und der Antwortvariablen von den anderen Faktoren im Term ab. In diesem Fall sollten Sie die Haupteffekte nicht interpretieren, ohne dabei den Wechselwirkungseffekt zu berücksichtigen.
- Quadrierte Terme
- Wenn ein Koeffizient für einen quadrierten Term signifikant ist, können Sie schlussfolgern, dass die Beziehung zwischen dem Faktor und der Antwortvariablen einer gekrümmten Linie folgt.
- Kovariaten
- Wenn der Koeffizient für eine Kovariate statistisch signifikant ist, können Sie schlussfolgern, dass die Assoziation zwischen der Antwortvariablen und der Kovariaten statistisch signifikant ist.
- Blöcke
- Wenn der Koeffizient für einen Block statistisch signifikant ist, können Sie schlussfolgern, dass sich die Linkfunktion für den Block vom Durchschnittswert unterscheidet.
Kodierte Koeffizienten
| Term | Koef | SE Koef | VIF |
|---|---|---|---|
| Konstante | 2,394 | 0,145 | |
| Backzeit | 0,7349 | 0,0538 | 1,11 |
| Backtemperatur 2 | 0,5451 | 0,0541 | 1,20 |
| Backzeit*Backzeit | -0,384 | 0,153 | 1,04 |
| Backzeit*Backtemperatur 2 | -0,5106 | 0,0562 | 1,24 |
Wichtigste Ergebnisse: Koeffizienten
In diesen Ergebnissen sind die Koeffizienten für Backzeit und Backtemperatur 2 positive Zahlen. Der Koeffizient für den quadrierten Term von Backzeit und der Koeffizient für den Wechselwirkungsterm zwischen Backzeit und Backtemperatur 2 sind negative Zahlen. Im Allgemeinen gilt bei einem zunehmenden Wert des Terms: Positive Koeffizienten steigern die Wahrscheinlichkeit des Ereignisses, während negative Koeffizienten die Wahrscheinlichkeit des Ereignisses verringern.
Varianzanalyse
| Quelle | DF | Kor Abw | Kor MW | Chi-Quadrat | p-Wert |
|---|---|---|---|---|---|
| Modell | 4 | 737,452 | 184,363 | 737,45 | 0,000 |
| Backzeit | 1 | 203,236 | 203,236 | 203,24 | 0,000 |
| Backtemperatur 2 | 1 | 100,432 | 100,432 | 100,43 | 0,000 |
| Backzeit*Backzeit | 1 | 6,770 | 6,770 | 6,77 | 0,009 |
| Backzeit*Backtemperatur 2 | 1 | 80,605 | 80,605 | 80,61 | 0,000 |
| Fehler | 45 | 32,276 | 0,717 | ||
| Gesamt | 49 | 769,728 |
Wichtigste Ergebnisse: p-Wert
In diesen Ergebnissen sind die Haupteffekte für Backzeit und Backtemperatur 2 auf dem Niveau 0,05 statistisch signifikant. Sie können schlussfolgern, dass zwischen Änderungen dieser Variablen und Änderungen der Antwortvariablen eine Assoziation besteht. Da im Modell Terme höherer Ordnung enthalten sind, wird der Effekt dieser Faktoren von den Koeffizienten für die Haupteffekte nicht vollständig beschrieben.
Der quadrierte Term für Backzeit ist signifikant. Sie können schlussfolgern, dass eine Assoziation zwischen Änderungen dieser Variablen und Änderungen der Antwortvariablen besteht; die Assoziation ist jedoch nicht linear.
Der Wechselwirkungseffekt zwischen Backzeit und Backtemperatur 2 ist signifikant. Sie können schlussfolgern, dass der Effekt von Änderungen in Backzeit auf die Farbe von der Stufe von Backtemperatur 2 abhängt. Analog dazu können Sie schlussfolgern, dass der Effekt von Änderungen in Backtemperatur 2 auf die Farbe von der Stufe von Backzeit abhängt.
Schritt 3: Verstehen der Effekte der Prädiktoren
- Chancenverhältnisse für stetige Prädiktoren
- Chancenverhältnisse größer als 1 weisen darauf hin, dass das Ereignis mit umso größerer Wahrscheinlichkeit eintritt, je größer der Prädiktor ist. Chancenverhältnisse kleiner als 1 weisen darauf hin, dass das Ereignis mit umso geringerer Wahrscheinlichkeit eintritt, je größer der Prädiktor ist.
Chancenverhältnisse für stetige Prädiktoren
Änderungseinheit Chancenverhältnis 95%-KI Backzeit 2 * (*; *) Backtemperatur 2 15 2,1653 (1,9652; 2,3858) Wichtigstes Ergebnis: Chancenverhältnis
In diesen Ergebnissen weist das Modell drei Terme auf, anhand derer prognostiziert wird, ob die Farbe des Gebäcks den Qualitätsstandards entspricht: Backzeit, Backtemperatur 2 und der quadrierte Term für Backzeit. In diesem Beispiel stellt eine akzeptable Farbe das Ereignis dar.
Die Einheit der Änderung zeigt die Differenz für eine kodierte Einheit im Versuchsplan in natürlichen Einheiten an. In natürlichen Einheiten beträgt die tiefe Stufe von Backtemperatur 2 beispielsweise 127. Die hohe Stufe liegt bei 157 Grad. Der Abstand von der tiefen Stufe zum Mittelpunkt stellt eine Änderung um eine kodierte Einheit dar. In diesem Fall beläuft sich der Abstand auf 15 Grad.
Das Chancenverhältnis für Backtemperatur 2 beträgt annähernd 2,17. Bei jedem Anstieg der Temperatur um 15 Grad steigt die Chance, dass die Gebäckfarbe akzeptabel ist, um etwa das 2,17-fache.
Das Chancenverhältnis für Backzeit fehlt, da das Modell den quadrierten Term für Backzeit enthält. Der Wert des Chancenverhältnisses ist nicht fest, da er vom Wert von Backzeit abhängt.
- Chancenverhältnisse für kategoriale Prädiktoren
-
Bei kategorialen Prädiktoren ist das Chancenverhältnis ein Vergleich der Chancen für das Eintreten des Ereignisses auf zwei verschiedenen Stufen des Prädiktors. Minitab richtet den Vergleich durch Auflisten der Stufen in zwei Spalten ein: Stufe A und Stufe B. Stufe B stellt die Referenzstufe für den Faktor dar. Chancenverhältnisse größer als 1 weisen darauf hin, dass das Ereignis mit größerer Wahrscheinlichkeit auf Stufe A eintritt. Chancenverhältnisse kleiner als 1 weisen darauf hin, dass das Ereignis mit geringerer Wahrscheinlichkeit auf Stufe A eintritt. Weitere Informationen zum Kodieren von kategorialen Prädiktoren finden Sie unter Kodierungsschemas für kategoriale Prädiktoren.
Chancenverhältnisse für kategoriale Prädiktoren
Stufe A Stufe B Chancenverhältnis 95%-KI Monat 2 1 1,1250 (0,0600; 21,0834) 3 1 3,3750 (0,2897; 39,3165) 4 1 7,7143 (0,7461; 79,7592) 5 1 2,2500 (0,1107; 45,7172) 6 1 6,0000 (0,5322; 67,6397) 3 2 3,0000 (0,2547; 35,3325) 4 2 6,8571 (0,6556; 71,7169) 5 2 2,0000 (0,0976; 41,0019) 6 2 5,3333 (0,4679; 60,7946) 4 3 2,2857 (0,4103; 12,7323) 5 3 0,6667 (0,0514; 8,6389) 6 3 1,7778 (0,2842; 11,1200) 5 4 0,2917 (0,0252; 3,3719) 6 4 0,7778 (0,1464; 4,1326) 6 5 2,6667 (0,2124; 33,4861) Wichtigstes Ergebnis: Chancenverhältnis
In diesen Ergebnissen ist der kategoriale Prädiktor der Monat, in dem die Hochsaison eines Hotels beginnt. Die Antwortvariable gibt an, ob ein Gast eine Reservierung storniert oder nicht. In diesem Beispiel stellt eine Stornierung das Ereignis dar. Das größte Chancenverhältnis beträgt etwa 7,71, wenn Stufe A gleich Monat 4 und Stufe B gleich Monat 1 ist. Das bedeutet, dass die Chance, dass ein Gast seine Reservierung storniert, in Monat 4 annähernd 8 Mal größer als in Monat 1 ist.
Schritt 4: Bestimmen, wie gut das Modell an die Daten angepasst ist
Um zu ermitteln, wie gut das Modell an die Daten angepasst ist, untersuchen Sie die Statistiken für die Güte der Anpassung in der Tabelle „Zusammenfassung des Modells“.
Hinweis
Viele Statistiken zur Übersicht des Modells und zur Güte der Anpassung werden davon beeinflusst, wie die Daten im Arbeitsblatt angeordnet sind und ob jede Zeile einen oder mehrere Versuche enthält. Der Hosmer-Lemeshow-Test wird durch die Anordnung der Daten nicht beeinflusst und liefert bei einem Versuch pro Zeile ähnliche Ergebnisse wie bei mehreren Versuchen pro Zeile. Weitere Informationen finden Sie unter Wie wirken sich Datenformate bei der binären logistischen Regression auf die Güte der Anpassung aus?.
- R-Qd der Abweichung
-
Je höher das R2 der Abweichung ausfällt, desto besser ist das Modell an die Daten angepasst. Das R2 der Abweichung liegt immer zwischen 0 % und 100 %.
Das R2 der Abweichung nimmt beim Einbinden zusätzlicher Terme in ein Modell stets zu. Das beste Modell mit fünf Termen weist beispielsweise immer ein R2 der Abweichung auf, das mindestens so hoch wie das des besten Modells mit vier Prädiktoren ist. Daher ist das R2 der Abweichung am nützlichsten, wenn Sie Modelle derselben Größe vergleichen.
Die Anordnung der Daten beeinflusst den Wert des R2 der Abweichung. Das R2 der Abweichung ist im Allgemeinen für Daten mit mehreren Versuchen pro Zeile höher als für Daten mit einem einzigen Versuch pro Zeile. Werte des R2 der Abweichung sind nur bei Modellen vergleichbar, in denen dasselbe Datenformat verwendet wird.
Statistiken für die Güte der Anpassung sind nur eines der Maße für die Güte der Anpassung des Modells an die Daten. Selbst wenn ein Modell einen erwünschten Wert aufweist, sollten Sie die Residuendiagramme und die Tests auf Güte der Anpassung untersuchen, um zu beurteilen, wie gut das Modell an die Daten angepasst ist.
- R-Qd(kor) der Abweichung
-
Verwenden Sie das korrigierte R2 der Abweichung, wenn Sie Modelle vergleichen möchten, die eine unterschiedliche Anzahl von Termen enthalten. Das R2 der Abweichung nimmt beim Einbinden eines Terms in das Modell stets zu. Der Wert des korrigierten R2 der Abweichung berücksichtigt die Anzahl der Terme im Modell, was die Auswahl des richtigen Modells erleichtert.
- AIC, AICc und BIC
- Anhand des AIC, des AICc und des BIC können Sie verschiedene Modelle vergleichen. Bei jeder dieser Statistiken sind kleinere Werte erwünscht. Das Modell mit dem kleinsten Wert für eine Gruppe von Prädiktoren ist jedoch nicht zwangsläufig gut an die Daten angepasst. Verwenden Sie daher auch die Tests auf die Güte der Anpassung und die Residuendiagramme, um zu beurteilen, wie gut ein Modell an die Daten angepasst ist.
Zusammenfassung des Modells
| R-Qd der Abweichung | R-Qd(kor) der Abweichung | AIC | AICc | BIC |
|---|---|---|---|---|
| 95,81% | 95,16% | 243,85 | 245,80 | 255,32 |
Wichtigste Ergebnisse: R-Qd der Abweichung, R-Qd(kor) der Abweichung, AIC, AICc, BIC
In diesen Ergebnissen erklärt das Modell 95,81 % der Gesamtabweichung in der Antwortvariablen. Für diese Daten gibt das R2 der Abweichung an, dass das Modell gut an die Daten angepasst ist. Wenn Sie weitere Modelle mit anderen Termen anpassen, verwenden Sie das korrigierte R2 der Abweichung sowie das AIC, das AICc und das BIC, um zu vergleichen, wie gut die Modelle an die Daten angepasst sind.
Schritt 5: Bestimmen, ob das Modell nicht an Ihre Daten angepasst ist
- Falsche Linkfunktion
- Fehlender Term höherer Ordnung für Variablen im Modell
- Fehlender Prädiktor, der nicht im Modell enthalten ist
- Überdispersion
Wenn die Abweichung statistisch signifikant ist, können Sie eine andere Linkfunktion verwenden oder die Terme im Modell ändern.
- Abweichung: Der p-Wert für den Abweichungstest ist für Daten mit einem Versuch pro Zeile tendenziell kleiner als für Daten mit mehreren Versuchen pro Zeile und nimmt generell mit der Anzahl der Versuche pro Zeile ab. Für Daten mit einem Versuch pro Zeile sind die Ergebnisse des Hosmer-Lemeshow-Tests zuverlässiger.
- Pearson: Die vom Pearson-Test verwendete Approximation an die Chi-Quadrat-Verteilung ist ungenau, wenn die erwartete Anzahl von Ereignissen pro Zeile in den Daten klein ist. Daher ist der Test auf Güte der Anpassung nach Pearson ungenau, wenn die Daten im Format mit einem Versuch pro Zeile vorliegen.
- Hosmer-Lemeshow: Der Hosmer-Lemeshow-Test hängt nicht wie die anderen Tests von der Anzahl der Versuche pro Zeile in den Daten ab. Wenn die Daten nur wenige Versuche pro Zeile aufweisen, ist der Hosmer-Lemeshow-Test ein zuverlässigerer Indikator dafür, wie gut das Modell an die Daten angepasst ist.
Tests auf Güte der Anpassung
| Test | DF | Chi-Quadrat | p-Wert |
|---|---|---|---|
| Abweichung | 44 | 32,26 | 0,905 |
| Pearson | 44 | 31,98 | 0,911 |
| Hosmer-Lemeshow | 7 | 4,18 | 0,758 |
Wichtigste Ergebnisse für das Ereignis-/Versuchsformat: Informationen zur Antwortvariablen, Abweichungstest, Pearson-Test, Hosmer-Lemeshow-Test
In diesen Ergebnisse weisen alle Tests auf Güte der Anpassung p-Werte auf, die über dem üblichen Signifikanzniveau 0,05 liegen. Die Tests liefern keine Anzeichen dafür, dass die prognostizierten Wahrscheinlichkeiten auf eine Weise von den beobachteten Wahrscheinlichkeiten abweichen, die mit der Binomialverteilung nicht prognostiziert wird.
