In diesem Thema
Versuchsplanmatrix
Minitab generiert für jeden Versuchsplan eine Versuchsplanmatrix. Die erste Spalte enthält ausschließlich Einsen für den konstanten Term. Wenn der Versuchsplan in k Blöcke aufgeteilt ist, liegen (k − 1) Spalten für Blöcke vor. Minitab verwendet dieselbe Methode der Blockkodierung wie in faktoriellen Modellen. Es folgt jeweils eine Spalte für jeden Haupteffekt. Terme mit kategorialen Faktoren können mehrere Spalten aufweisen. Wenn das Modell quadrierte Terme aufweist, ist für jeden quadrierten Term eine Spalte vorhanden. Die Spalte für einen quadrierten Term ist das Produkt des entsprechenden Faktors mit sich selbst. Wenn das Modell Wechselwirkungsterme enthält, ist für jeden Wechselwirkungsterm eine Spalte vorhanden. Wechselwirkungen mit kategorialen Faktoren können mehrere Spalten aufweisen. Die Spalte für einen Wechselwirkungsterm entspricht dem Produkt der beiden gekreuzten Spalten.
Wenn Minitab einige Terme entfernt, weil sie von den Daten nicht unterstützt werden, sind die betreffenden Terme nicht in der gespeicherten Versuchsplanmatrix enthalten. Die gespeicherten Spalten stimmen mit den angezeigten Koeffizienten überein.
Koeffizient (Koef)
Ausgedrückt unter Verwendung von Matrizen lautet die Formel zum Berechnen des Vektors von Koeffizienten im Modell wie folgt:

Notation
| Begriff | Beschreibung |
|---|---|
| X | Versuchsplanmatrix |
| Y | Vektor der Antwortvariablen |
Box-Cox-Transformation
Bei der Box-Cox-Transformation werden Lambda-Werte (siehe unten) ausgewählt, die die Summe der Quadrate der Residuen minimieren. Die resultierende Transformation ist Y λ, wenn λ ≠ 0, und ln(Y), wenn λ = 0. Wenn λ < 0, multipliziert Minitab zudem die transformierte Antwortvariable mit −1, um die Reihenfolge aus der nicht transformierten Antwortvariablen beizubehalten.
Minitab sucht einen optimalen Wert zwischen −2 und 2. Werte, die außerhalb dieses Intervalls liegen, führen möglicherweise nicht zu einer besseren Anpassung.
Hier finden Sie einige der gängigsten Transformationen, wobei Y′ das transformierte Y der Daten darstellt:
| Lambda-Wert (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 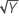 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
