In diesem Thema
Anpassung
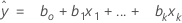
Notation
| Begriff | Beschreibung |
|---|---|
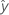 | angepasster Wert |
| xk | k-ter Term. Jeder Term kann ein einzelner Prädiktor, ein Polynomialterm oder ein Wechselwirkungsterm sein. |
| bk | Schätzwert des k-ten Regressionskoeffizienten |
Standardfehler des angepassten Werts (SE Anpassung)
Der Standardfehler des angepassten Werts in einem Regressionsmodell mit einem Prädiktor wird wie folgt ausgedrückt:
Der Standardfehler des angepassten Werts in einem Regressionsmodell mit mehreren Prädiktoren wird wie folgt ausgedrückt:
Fügen Sie für die gewichtete Regression die Gewichtsmatrix in die Gleichung ein:
Wenn die Daten über einen Testdatensatz oder eine K-Falten-Kreuzvalidierung verfügen, sind die Formeln identisch. Der Wert von s2 stammt aus den Trainingsdaten. Die Designmatrix und die Gewichtsmatrix stammen ebenfalls aus den Trainingsdaten.
Notation
| Begriff | Beschreibung |
|---|---|
| s2 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xi | i-ter predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| X =0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
Residuen
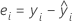
Notation
| Begriff | Beschreibung |
|---|---|
| yi | i-ter beobachteter Wert der Antwortvariablen |
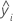 | i-ter angepasster Wert der Antwortvariablen |
Standardisiertes Residuum (Std. Resid)
Standardisierte Residuen werden auch als intern studentisierte Residuen bezeichnet.
Formel
Notation
| Begriff | Beschreibung |
|---|---|
| ei | i-tes Residuum |
| hi | i-tes Diagonalelement von X(X'X)–1X' |
| s2 | mittleres Fehlerquadrat |
| X | Designmatrix |
| X' | transponierte Designmatrix |
Entfernte (studentisierte) Residuen
Diese werden auch als extern studentisierte Residuen bezeichnet. Die Formel lautet wie folgt:
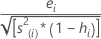
Die Formel kann auch wie folgt ausgedrückt werden:
In dem Modell, mit dem die i-te Beobachtung geschätzt wird, wird die i-te Beobachtung aus dem Datensatz entfernt. Daher kann die i-te Beobachtung den Schätzwert nicht beeinflussen. Jedes entfernte Residuum hat eine Student-t-Verteilung mit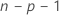 
Freiheitsgraden.
Notation
| Begriff | Beschreibung |
|---|---|
| ei | i-tes Residuum |
| s(i)2 | mittlerer quadrierter Fehler, der ohne die i-te Beobachtung berechnet wurde |
| hi | i-tes Diagonalelement von X(X'X)–1X' |
| n | Anzahl der Beobachtungen |
| p | Anzahl der Terme, einschließlich der Konstanten |
| SSE | Summe der Quadrate für Fehler |
Konfidenzintervall
Der Bereich, in dem der geschätzte Mittelwert der Antwortvariablen bei einer gegebenen Gruppe von Werten der Prädiktorvariablen erwartet wird. Das Intervall wird durch eine untere und eine obere Grenze definiert, die Minitab aus dem Konfidenzniveau und dem Standardfehler der Anpassungen berechnet.
Dabei gilt Folgendes:
Notation
| Begriff | Beschreibung |
|---|---|
| α | ausgewählter Alpha-Wert |
| n | Anzahl der Beobachtungen |
| p | Anzahl der Parameter |
| s2 | mittleres Fehlerquadrat |
| s2{b} | Varianz-Kovarianz-Matrix der Koeffizienten |
Prognoseintervall
Der Bereich, in dem der prognostizierte Wert der Antwortvariablen für eine neue Beobachtung erwartet wird. Das Intervall wird durch eine untere und eine obere Grenze definiert, die Minitab aus dem Konfidenzniveau und dem Standardfehler der Prognose berechnet. Das Prognoseintervall ist immer breiter als das Konfidenzintervall. Dies ist auf die zusätzliche Ungewissheit beim Prognostizieren eines einzelnen Werts der Antwortvariablen gegenüber dem Mittelwert der Antwortvariablen zurückzuführen.
Die Formel lautet wie folgt: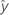 
0+ t(1 – α / 2; n – p) s(prog)
Notation
| Begriff | Beschreibung |
|---|---|
| α | ausgewählter Alpha-Wert |
| n | Anzahl der Beobachtungen |
| p | Anzahl der Prädiktoren |
| s(prog) |  |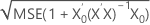
