Ein Verpackungstechniker muss sicherstellen, dass die Abdichtungen an Kunststoffbeuteln mit einem Produkt ausreichend stark sind, um Undichtigkeiten zu verhindern, jedoch nicht so stark, dass der Beutel vom Verbraucher nicht geöffnet werden kann. Die Beutel halten chirurgische Instrumente trocken und steril, bis sie geöffnet werden. Der Techniker möchte die Abdichtungsstärke auf einen Wert zwischen 20 und 32 Pfund (Unter- und Obergrenze) mit einem Sollwert von 26 Pfund optimieren. Zudem möchte er die Streuung der Abdichtungsstärke so minimieren, dass sie höchstens 1 beträgt. Der Techniker ermittelt, dass Schienentemperatur, Verweilzeit und Schienendruck Faktoren sind, die zur Stärke der Abdichtung beitragen. Zudem bestimmt er, dass Schienentemperatur, Verweilzeit und Materialtemperatur wichtige Faktoren sind, die die Streuung beeinflussen. Der Techniker entwirft ein zentral zusammengesetztes Wirkungsflächenexperiment, um die Einflussfaktoren für Stärke und Streuung der Abdichtung zu untersuchen. Er analysiert die Streuung der Abdichtung anhand einer Transformation mit dem natürlichem Logarithmus.
Der Techniker erfasst Daten und analysiert den Versuchsplan, um festzustellen, welche Faktoren sich auf die Abdichtungsstärke auswirken.
- Öffnen Sie die Beispieldaten Abdichtungsstärke.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antworten die Spalte Festigkeit ein.
- Klicken Sie auf Grafiken.
- Wählen Sie unter Residuendiagramme die Option Vier-in-eins aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
In der Tabelle der Varianzanalyse sind die p-Werte für „SchienenT*SchienenT“, „VWZeit*VWZeit“ und „SchienenT*VWZeit“ signifikant. Der Techniker kann erwägen, das Modell zu reduzieren, um die nicht signifikanten Terme zu entfernen. Weitere Informationen finden Sie unter Modellreduzierung.
Das R2 gibt an, dass das Modell 78,58 % der Varianz der Stärke erklärt; dies weist darauf hin, dass das Modell angemessen an die Daten angepasst ist. Das prognostizierte R2 von 0 deutet darauf hin, dass dieses Modell übermäßig angepasst ist – ein Hinweis darauf, dass das Modell reduziert werden sollte.
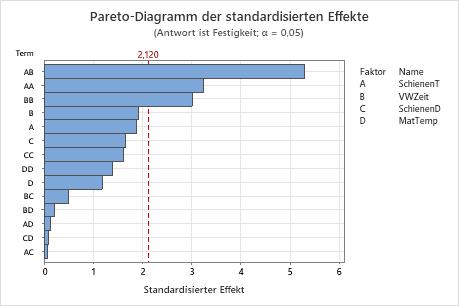
Mit Hilfe des Pareto-Diagramms der Effekte können Sie die wichtigen Effekte in einer grafischen Darstellung identifizieren und die relative Größe der verschiedenen Effekte miteinander vergleichen. Außerdem ist hier ersichtlich, dass „SchienenT*VWZeit“ (AB) den größten Effekt darstellt, da der entsprechende Balken am längsten ist.
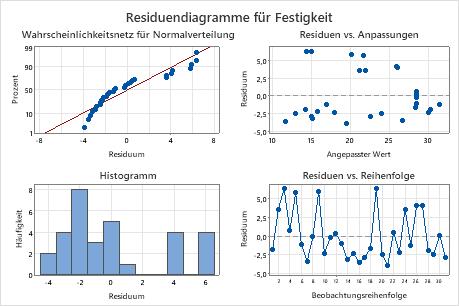
In den Residuendiagrammen folgen die Punkte im Wahrscheinlichkeitsnetz für Normalverteilung nicht der Geraden. Durch Reduzieren des Modells können Sie dieses Problem u. U. beheben.
Kodierte Koeffizienten
| Term | Koef | SE Koef | t-Wert | p-Wert | VIF |
|---|---|---|---|---|---|
| Konstante | 28,44 | 1,66 | 17,09 | 0,000 | |
| SchienenT | 1,685 | 0,899 | 1,87 | 0,079 | 1,00 |
| VWZeit | -1,719 | 0,899 | -1,91 | 0,074 | 1,00 |
| SchienenD | 1,481 | 0,899 | 1,65 | 0,119 | 1,00 |
| MatTemp | 1,060 | 0,899 | 1,18 | 0,255 | 1,00 |
| SchienenT*SchienenT | -2,662 | 0,823 | -3,23 | 0,005 | 1,03 |
| VWZeit*VWZeit | -2,476 | 0,823 | -3,01 | 0,008 | 1,03 |
| SchienenD*SchienenD | -1,329 | 0,823 | -1,61 | 0,126 | 1,03 |
| MatTemp*MatTemp | -1,151 | 0,823 | -1,40 | 0,181 | 1,03 |
| SchienenT*VWZeit | -5,81 | 1,10 | -5,28 | 0,000 | 1,00 |
| SchienenT*SchienenD | -0,09 | 1,10 | -0,08 | 0,938 | 1,00 |
| SchienenT*MatTemp | -0,14 | 1,10 | -0,13 | 0,902 | 1,00 |
| VWZeit*SchienenD | 0,55 | 1,10 | 0,50 | 0,624 | 1,00 |
| VWZeit*MatTemp | 0,24 | 1,10 | 0,22 | 0,832 | 1,00 |
| SchienenD*MatTemp | -0,10 | 1,10 | -0,09 | 0,929 | 1,00 |
Zusammenfassung des Modells
| S | R-Qd | R-Qd(kor) | R-Qd(prog) |
|---|---|---|---|
| 4,40228 | 78,58% | 59,84% | 0,00% |
Varianzanalyse
| Quelle | DF | Kor SS | Kor MS | F-Wert | p-Wert |
|---|---|---|---|---|---|
| Modell | 14 | 1137,51 | 81,251 | 4,19 | 0,004 |
| Linear | 4 | 218,65 | 54,662 | 2,82 | 0,060 |
| SchienenT | 1 | 68,13 | 68,129 | 3,52 | 0,079 |
| VWZeit | 1 | 70,94 | 70,939 | 3,66 | 0,074 |
| SchienenD | 1 | 52,62 | 52,616 | 2,71 | 0,119 |
| MatTemp | 1 | 26,96 | 26,963 | 1,39 | 0,255 |
| Quadratisch | 4 | 372,07 | 93,018 | 4,80 | 0,010 |
| SchienenT*SchienenT | 1 | 202,61 | 202,611 | 10,45 | 0,005 |
| VWZeit*VWZeit | 1 | 175,32 | 175,318 | 9,05 | 0,008 |
| SchienenD*SchienenD | 1 | 50,52 | 50,522 | 2,61 | 0,126 |
| MatTemp*MatTemp | 1 | 37,87 | 37,866 | 1,95 | 0,181 |
| 2-Faktor-Wechselwirkung | 6 | 546,79 | 91,132 | 4,70 | 0,006 |
| SchienenT*VWZeit | 1 | 540,47 | 540,470 | 27,89 | 0,000 |
| SchienenT*SchienenD | 1 | 0,12 | 0,121 | 0,01 | 0,938 |
| SchienenT*MatTemp | 1 | 0,30 | 0,305 | 0,02 | 0,902 |
| VWZeit*SchienenD | 1 | 4,84 | 4,840 | 0,25 | 0,624 |
| VWZeit*MatTemp | 1 | 0,90 | 0,899 | 0,05 | 0,832 |
| SchienenD*MatTemp | 1 | 0,16 | 0,160 | 0,01 | 0,929 |
| Fehler | 16 | 310,08 | 19,380 | ||
| Fehlende Anpassung | 10 | 308,20 | 30,820 | 98,51 | 0,000 |
| Reiner Fehler | 6 | 1,88 | 0,313 | ||
| Gesamt | 30 | 1447,60 |
Regressionsgleichung in nicht kodierten Einheiten
| Festigkeit | = | -289,3 + 2,287 SchienenT + 206,6 VWZeit + 0,124 SchienenD + 0,594 MatTemp - 0,00426 SchienenT*SchienenT - 39,6 VWZeit*VWZeit - 0,000532 SchienenD*SchienenD - 0,00288 MatTemp*MatTemp - 0,930 SchienenT*VWZeit - 0,000070 SchienenT*SchienenD - 0,00028 SchienenT*MatTemp + 0,0440 VWZeit*SchienenD + 0,047 VWZeit*MatTemp - 0,00010 SchienenD*MatTemp |
|---|
Anpassungen und Bewertung für ungewöhnliche Beobachtungen
| Beob | Festigkeit | Anpassung | Resid | Std. Resid | |
|---|---|---|---|---|---|
| 3 | 20,69 | 14,43 | 6,26 | 2,20 | R |
| 5 | 27,43 | 21,72 | 5,71 | 2,01 | R |
| 9 | 25,99 | 20,16 | 5,83 | 2,05 | R |
| 19 | 21,38 | 15,10 | 6,28 | 2,21 | R |