In diesem Thema
Simplex-Zentroid-Versuchspläne
Ein Simplex-Zentroid-Versuchsplan für eine Mischung mit q Komponenten besteht aus 2**q – 1 Punkten. Die folgenden Versuchsplanpunkte sind vorhanden:
- Alle Punkte (x1, x2, ..., xq), an denen eine Komponente xi = 1 ist und alle anderen 0 sind. Diese Punkte werden als Eckpunkte bezeichnet.
- Alle Punkte, an denen eine Komponente xi = 1/2 und eine weitere Komponente xj = 1/2 ist und alle anderen 0 sind.
- Alle Punkte, an denen eine Komponente xi = 1/3, eine weitere Komponente xj = 1/3 und eine weitere Komponente xk = 1/3 ist und alle anderen 0 sind.
- Dieses Muster setzt sich fort, bis alle Komponenten gleich 1/q sind. Dieser letzte Punkt (an dem alle Komponenten gleich sind) wird als Zentrum oder Zentroid des Versuchsplans bezeichnet.
Simplexgitter-Versuchspläne
| Gittergrad (m) | Anzahl der Komponenten (q) |
|---|---|
| 1 | 2 bis 20 |
| 2 | 2 bis 20 |
| 3 | 2 bis 17 |
| 4 | 2 bis 11 |
| 5 | 2 bis 8 |
| 6 | 2 bis 7 |
| 7 | 2 bis 6 |
| 8 | 2 bis 5 |
| 9 | 2 bis 5 |
| 10 | 2 bis 5 |
Mischungsversuchspläne mit Begrenzungen
Minitab erzeugt die Begrenzungen für den eingeschränkten Raum des Versuchsplans anhand des XVERT-Algorithmus und berechnet dann die Zentroidpunkte bis zum angegebenen Grad anhand des CONAEV-Algorithmus nach Piepel. Weitere Informationen finden Sie in Cornell1 und St. John2.
- J. A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
- R. C. St. John (1984). „Experiments With Mixtures in Conditioning and Ridge Regression,“ Journal of Quality Technology 16, S.81–96.
Typen von Experimenten
Mit Minitab können Sie Daten aus drei Typen von Experimenten analysieren:
| Typ | Wert der Antwortvariablen ist abhängig |
| Mischung | nur von den relativen Anteilen der Komponenten. |
| Mischung mit Prozessvariablen | von den Komponenten und den Prozessvariablen. Prozessvariablen sind Faktoren in einem Experiment, die nicht Teil der Mischung sind, sich aber auf die Antwortvariable auswirken können. |
| Mischungsmengen | von den relativen Anteilen der Komponenten und der Gesamtmenge der Mischung. |
Positionieren von Gitterpunkten in erweiterten Mischungsversuchsplänen
Minitab erweitert den Versuchsplan (fügt Punkte hinzu), wie nachfolgend dargestellt. Jeder hinzugefügte Punkt wird in der Mitte zwischen einem Eckpunkt und dem Zentrum des Versuchsplans angeordnet.
Durch Erweitern eines Versuchsplans können Sie Informationen zu den Antwortvariablen im Inneren des Versuchsplans erhalten, anstatt sich nur auf die Punkte an den Kanten zu verlassen.
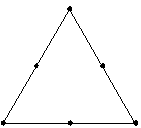
Nicht erweitert
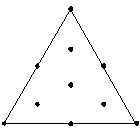
Erweitert
Konvertieren von Komponenteneinheiten
In Minitab kann das Erstellen von Versuchsplänen und die Analyse der Daten in Mengen-, Anteils- und Pseudokomponenteneinheiten erfolgen.
Um Daten aus einer Mengen- in eine Anteilseinheit zu konvertieren, verwenden Sie die folgende Formel:
- Anteil = Menge/Gesamt
Wenn der Gesamtwert = 1 ist, dann gilt: Anteilseinheiten = Mengeneinheiten.
Um Anteilseinheiten in Pseudokomponenteneinheiten zu konvertieren, verwenden Sie die folgende Formel:
- Pseudo = (Anteil – Untergrenze) / (1 – Summe der Untergrenzen)
- Anteil = Pseudo * (1 – Summe der Untergrenzen) + Untergrenze
Wenn alle Untergrenzen = 0 sind, dann gilt: Pseudokomponenteneinheiten = Anteilseinheiten.
Modellterme
Mischungsversuchspläne enthalten viele Typen von Modelltermen. Die Terme und ihre Darstellungen sind:
| Modell | Terme |
| Linear | A B C |
| Quadratisch | Linear + AB AC BC |
| Speziell kubisch | Quadratisch + ABC |
| Vollständig kubisch | Speziell kubisch + AB(A–B) AC(A–C) BC(B–C) |
| Speziell biquadratisch | Quadratisch + AABC ABBC ABCC |
| Vollständig biquadratisch | Speziell biquadratisch + AB(A–B) AC(A–C) BC(B–C) AB(A–B)2 AC(A–C)2 BC(B–C)2 |
Beachten Sie, dass es in Mischungsmodellen keinen konstanten Term gibt. Zu den inversen Termen zählen 1/A, 1/B, 1/C usw.
