In diesem Thema
Koeffizient (Koef)
Minitab berechnet die Koeffizienten anhand der Schätzung der kleinsten Quadrate.
Als Matrix ausgedrückt entsprechen die Schätzungen der kleinsten Quadrate für Koeffizienten:
b = (X'X)–1X'y
Weitere Informationen zu Koeffizienten in Modellen höherer Ordnung finden Sie in Cornell1.
Notation
| Begriff | Beschreibung |
|---|---|
| X | Versuchsplanmatrix |
| y | Spalte der Antwortvariablen |
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
Standardfehler des Koeffizienten (SE Koef)
Bei der einfachen linearen Regression lautet der Standardfehler des Koeffizienten:
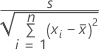
Die Standardfehler der Koeffizienten für die multiple Regression entsprechen den Quadratwurzeln der Diagonalelemente dieser Matrix:
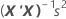
Notation
| Begriff | Beschreibung |
|---|---|
| xi | i-ter Prädiktorwert |
 | Mittelwert des Prädiktors |
| X | Designmatrix |
| X' | transponierte Designmatrix |
| s2 | Mittleres Fehlerquadrat |
t-Wert
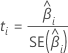
Notation
| Begriff | Beschreibung |
|---|---|
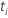 | Teststatistik für den  Koeffizienten Koeffizienten |
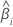 |  geschätzter Koeffizient geschätzter Koeffizient |
 | Standardfehler des  geschätzten Koeffizienten geschätzten Koeffizienten |
p-Wert – Koeffiziententabelle
Der beidseitige p-Wert für die Nullhypothese, dass ein Regressionskoeffizient gleich 0 ist, wird wie folgt ausgedrückt:
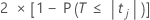
Die Freiheitsgrade sind die Freiheitsgrade für Fehler und werden wie folgt ausgedrückt:
n – p
Notation
| Begriff | Beschreibung |
|---|---|
 | Kumulative Verteilungsfunktion der t-Verteilung mit Freiheitsgraden, die den Freiheitsgraden für Fehler entsprechen |
| tj | t-Statistik für den j-ten Koeffizienten |
| n | Anzahl der Beobachtungen im Datensatz |
| p | Summe der Freiheitsgrade für die Terme |
Varianzinflationsfaktor (VIF)
Der VIF lässt sich durch Regression der einzelnen Prädiktoren auf die jeweils übrigen Prädiktoren und Aufzeichnen des R2 berechnen.
Formel
Für Prädiktor xj lautet der VIF:

Notation
| Begriff | Beschreibung |
|---|---|
| R2( xj) | Determinationskoeffizient mit xj als Antwortvariable und den anderen Termen im Modell als Prädiktoren |
