Forscher in einem Lebensmittellabor möchten ein Rezept für Käsefondue weiterentwickeln. Hierzu sollen der Geschmack verbessert, die anhaftende Menge am in das Fondue eingetauchten Brot maximiert und die am Boden des Topfes angebrannte Menge minimiert werden. Die Forscher entwerfen ein Experiment mit einem Mischungsversuchsplan mit Begrenzungen, um die Auswirkungen des Mischungsverhältnisses sowie der Serviertemperatur zu untersuchen.
- Öffnen Sie die Beispieldaten Fonduerezept.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antworten die Spalte Geschmack ein.
- Wählen Sie unter Modelltyp die Option Mischungskomponenten und Prozessvariablen aus.
- Wählen Sie unter Komponenten analysieren in die Option Anteilen aus.
- Wählen Sie unter Modellanpassungsmethode die Option Regression für Mischungen aus.
- Klicken Sie auf Terme.
- Verschieben Sie die folgenden Terme mit Hilfe der Pfeiltasten nach Ausgewählte Terme: Emmentaler, Greyerzer, Brühe, AB, BC, A*X1, B*X1, C*X1.
- Klicken Sie auf OK und dann auf Grafiken.
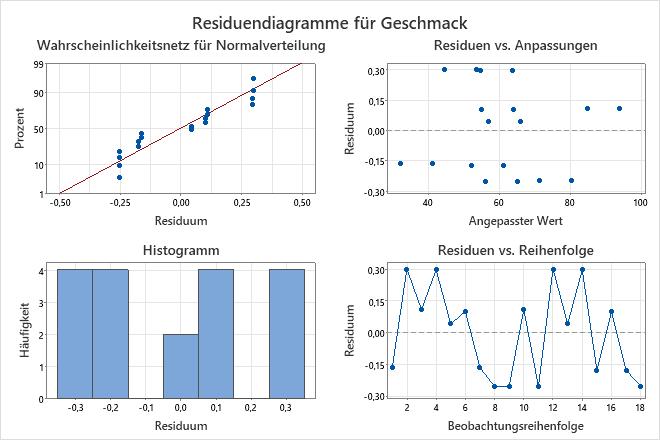
- Wählen Sie unter Residuendiagramme die Option Vier-in-eins aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
Da die p-Werte kleiner als das Signifikanzniveau 0,05 sind, können die Wissenschaftler schlussfolgern, dass die Wechselwirkungseffekte statistisch signifikant sind.
Die positiven Koeffizenten für die Wechselwirkungsterme mit zwei Komponenten weisen darauf hin, dass sich die beiden Komponentenmischungen synergetisch verhalten. Dies bedeutet, dass die mittlere Geschmacksbewertung für die Mischung größer als der Wert ist, den Sie bei einer Berechnung des einfachen Mittelwerts der beiden Geschmacksbewertungen für die einzelnen reinen Mischungen erhalten würden.
Außerdem weist die Wechselwirkung zwischen den Zutaten und der Prozessvariable (Temperatur) darauf hin, dass sich die Geschmacksbewertungen der Mischungen abhängig von der Serviertemperatur unterscheidet.
Das R2 gibt an, dass das Modell 99,98 % der Streuung beim Geschmack erklärt; dies weist darauf hin, dass das Modell außerordentlich gut an die Daten angepasst ist.
Tipp
Um die Beziehungen zwischen den Komponenten/Prozessvariablen und der Antwortvariablen näher zu untersuchen, verwenden Sie Konturdiagramm, Wirkungsflächendiagramm und Ergebnisspurendiagramm.
Geschätzte Regressionskoeffizienten für Geschmack (Komponentenanteile)
| Term | Koef | SE Koef | t-Wert | p-Wert | VIF |
|---|---|---|---|---|---|
| Emmentaler | 104,874 | 0,667 | * | * | 15,94 |
| Greyerzer | 175,08 | 5,89 | * | * | 203,46 |
| Brühe | -8,810 | 0,659 | * | * | 26,04 |
| Emmentaler*Greyerzer | 59,2 | 10,3 | 5,75 | 0,000 | 57,33 |
| Greyerzer*Brühe | 30,04 | 9,00 | 3,34 | 0,008 | 109,44 |
| Emmentaler*Temperatur | 4,500 | 0,475 | 9,48 | 0,000 | 8,09 |
| Greyerzer*Temperatur | 4,500 | 0,679 | 6,62 | 0,000 | 2,71 |
| Brühe*Temperatur | 4,500 | 0,443 | 10,16 | 0,000 | 11,76 |
Zusammenfassung des Modells
| S | R-Qd | R-Qd(kor) | PRESS | R-Qd(prog) |
|---|---|---|---|---|
| 0,276960 | 99,98% | 99,97% | 2,65322 | 99,93% |
Varianzanalyse für Geschmack (Komponentenanteile)
| Quelle | DF | Seq SS | Kor SS | Kor MS | F-Wert | p-Wert |
|---|---|---|---|---|---|---|
| Regression | 7 | 3924,18 | 3924,18 | 560,597 | 7308,30 | 0,000 |
| Nur Komponente | ||||||
| Linear | 2 | 3557,10 | 741,33 | 370,664 | 4832,22 | 0,000 |
| Quadratisch | 2 | 2,58 | 2,58 | 1,289 | 16,80 | 0,001 |
| Emmentaler*Greyerzer | 1 | 1,72 | 2,53 | 2,532 | 33,01 | 0,000 |
| Greyerzer*Brühe | 1 | 0,85 | 0,85 | 0,855 | 11,14 | 0,008 |
| Komponente * Temperatur | ||||||
| Linear | 3 | 364,50 | 364,50 | 121,500 | 1583,95 | 0,000 |
| Emmentaler*Temperatur | 1 | 335,51 | 6,89 | 6,887 | 89,79 | 0,000 |
| Greyerzer*Temperatur | 1 | 21,07 | 3,37 | 3,365 | 43,87 | 0,000 |
| Brühe*Temperatur | 1 | 7,92 | 7,92 | 7,924 | 103,30 | 0,000 |
| Residuenfehler | 10 | 0,77 | 0,77 | 0,077 | ||
| Gesamt | 17 | 3924,94 |