In diesem Thema
Methode
Minitab verwendet zwei Methoden zum Analysieren der Standardabweichungen der Wiederholungs- oder Replikationsmessungen: kleinste Quadrate und Maximum-Likelihood. Beide Methoden basieren auf einem linearen Modell mit einer Log-Linkfunktion: ln(σ) = Aγ, wobei A die Versuchsplanmatrix und γ ein Vektor der zu schätzenden Parameter ist. Ein Vorteil der Log-Linkfunktion ist, dass die angepassten Werte immer positiv sind.
Die zwei Methoden führen zu identischen Ergebnissen im saturierten Modell, wenn die Anzahl der Parameter mit der Anzahl der Datenpunkte übereinstimmt.
Für die Schätzung nach der Methode der kleinsten Quadrate verwendet Minitab die Regression der gewichteten kleinsten Quadrate. Wenn die Anzahl der Wiederholungen oder Replikationen gleich ist, sind die Gewichtungen ebenfalls gleich.
Bei der MLE-Methode geht Minitab davon aus, dass die ursprünglichen Daten aus einer Normalverteilung stammen. Die Verteilung der Stichprobenvarianz ist mit der χ2-Verteilung verwandt.
Versuchsplanmatrix
Minitab verfolgt für die Versuchsplanmatrix denselben Ansatz wie im allgemeinen linearen Modell (GLM), bei dem das angegebene Modell mit einer Regression angepasst wird. Zunächst erstellt Minitab auf der Grundlage der Faktoren und des angegebenen Modells eine Versuchsplanmatrix. Die Spalten dieser Matrix (mit X bezeichnet) stellen die Terme im Modell dar.
Die Versuchsplanmatrix umfasst n Zeilen, wobei n die Anzahl der Beobachtungen ist, sowie mehrere Blöcke von Spalten, die den Termen im Modell entsprechen. Der erste Block steht für die Konstante und umfasst lediglich eine Spalte, die nur Einsen enthält. Der Block für einen stetigen Faktor enthält ebenfalls nur eine Spalte. Der Block von Spalten für einen kategorialen Faktor enthält r Spalten, wobei r den Freiheitsgraden für den Faktor entspricht.
Angenommen, es liegt ein teilfaktorieller Versuchsplan mit drei Faktoren vor, von denen jeder zwei Stufen aufweist. Das Modell enthält 3 Haupteffekte. Jede Zeile ist jeweils wie folgt kodiert:
| Blöcke | Faktor 1 | Faktor 2 | Faktor 3 |
|---|---|---|---|
| 1 | −1 | −1 | −1 |
| 1 | 1 | −1 | −1 |
| 1 | −1 | 1 | −1 |
| 1 | 1 | 1 | −1 |
| 1 | −1 | −1 | 1 |
| 1 | 1 | −1 | 1 |
| 1 | −1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Effekte
Geschätzte Effekte für jeden Faktor. Effekte werden nur für zweistufige Modelle und nicht für allgemeine faktorielle Modelle berechnet. Die Formel für den Effekt eines Faktors lautet wie folgt:
Effekt = Koeffizient * 2
Koeffizienten (Koef)
Die Schätzwerte der Regressionskoeffizienten der Grundgesamtheit in einer Regressionsgleichung. Für jeden Faktor berechnet Minitab k – 1 Koeffizienten, wobei k der Anzahl der Stufen im Faktor entspricht. Für ein zweistufiges vollfaktorielles Zwei-Faktor-Modell lauten die Formeln für die Koeffizienten der Faktoren und Wechselwirkungen wie folgt:


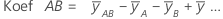
Der Standardfehler des Koeffizienten für dieses zweistufige, vollfaktorielle Zwei-Faktor-Modell wird wie folgt ausgedrückt:

Weitere Informationen zu Modellen mit mehr als zwei Faktoren oder Faktoren mit mehr als zwei Stufen finden Sie in Montgomery1.
Notation
| Begriff | Beschreibung |
|---|---|
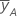 | Mittelwert von y auf der hohen Stufe von Faktor A |
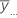 | Gesamtmittelwert aller Beobachtungen |
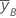 | Mittelwert von y auf der hohen Stufe von Faktor B |
 | Mittelwert von y auf den hohen Stufen von A und B |
| MSE | mittleres Fehlerquadrat (MSE) |
| n | Anzahl der Werte –1 und 1 (in der Kovarianzmatrix) für den geschätzten Term |
Gewichtete Regression
Bei der Regression der gewichteten kleinsten Quadrate handelt es sich um eine Methode zum Behandeln von Beobachtungen, deren Varianzen nicht konstant sind. Wenn die Varianzen nicht konstant sind, gelten für die Beobachtungen folgende Hinweise:
- Großen Varianzen sollten relativ kleine Gewichtungen zugewiesen werden.
- Kleinen Varianzen sollten relativ große Gewichtungen zugewiesen werden.
Die Gewichtungen spiegeln die Anzahl der Wiederholungen oder Replikationen wider, die zur Berechnung der einzelnen Standardabweichungen herangezogen werden. Standardabweichungen, die auf einer größeren Datenmenge basieren, haben eine größere Gewichtung.
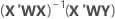
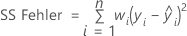
Notation
| Begriff | Beschreibung |
|---|---|
| X | Versuchsplanmatrix |
| X' | transponierte Versuchsplanmatrix |
| W | eine (n x n)-Matrix mit den Gewichtungen auf der Diagonalen |
| Y | Vektor der logarithmierten Standardabweichungen |
| n | Anzahl der Beobachtungen |
| wi | Gewichtung für die i-te Beobachtung |
| yi | logarithmierte Standardabweichung für die i-te Beobachtung |
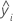 | angepasster Wert der logarithmierten Standardabweichung für die i-te Beobachtung |
Berechnen von Gewichtungen
Sie können die Gewichtungen zur Analyse des Lagemodells mit Hilfe von angepassten oder korrigierten Varianzen basierend auf dem Streuungsmodell berechnen und speichern.
- 1 / angepasste Varianz
- σ2(zwischen) + σ2 (innerhalb) / Anzahl der Wiederholungen
„Zwischen“ und „innerhalb“ beziehen sich auf einen Durchlauf des Experiments. Die Streuung innerhalb eines Durchlaufs ist der Wert, den Sie mit der Standardabweichung für Wiederholungsbeobachtungen messen. Die Streuung zwischen Durchläufen bezieht sich auf die zusätzlichen Streuungsquellen für neue Durchläufe.
Wenn Sie die Standardabweichung über Wiederholungen hinweg analysieren, passen Sie ein Modell an s (innerhalb) an. Wenn Replikationen vorliegen, kombiniert Minitab das Modell für σ2 (innerhalb) und die Varianz der Mittelwerte über Replikationen hinweg, um einen Schätzwert von σ2 (zwischen) zu erhalten. Anschließend wird der Schätzwert von σ2 (zwischen) erneut mit σ2 (innerhalb) / Anzahl der Wiederholungen kombiniert, um die Varianzschätzwerte für die Mittelwerte zu erhalten, die mit Ihrem Streuungsmodell übereinstimmen.
Bei diesem Ansatz wird angenommen, dass σ2 (zwischen) konstant ist und nicht von den Faktorstufen abhängt. Wenn diese Annahme nicht zutrifft, empfiehlt es sich möglicherweise, ein Modell an die Varianz von x anpassen, indem Sie „Analyse der Streuung vorbereiten“ mit  ausführen, um σ2 über Replikationen hinweg zu erhalten.
ausführen, um σ2 über Replikationen hinweg zu erhalten.
Wenn das Modell Kovariaten enthält, sollten Sie diese in der Varianz für Wiederholungen berücksichtigen. In der angepassten Varianz können keine Kovariaten berücksichtigt werden.
