Interpretieren der wichtigsten Ergebnisse für Streuung analysieren

Führen Sie die folgenden Schritte aus, um eine Streuungsanalyse zu interpretieren. Zu den wichtigsten Ausgaben zählen der p-Wert, die Koeffizienten, R² und die Residuendiagramme.

In diesem Thema

Schritt 1: Bestimmen, welche Terme am stärksten zur Streuung der Antwortvariablen beitragen
Schritt 2: Bestimmen, welche Terme statistisch signifikante Effekte auf die Antwortvariable haben
Schritt 3: Bestimmen, wie gut das Modell an die Daten angepasst ist
Schritt 4: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt

Schritt 1: Bestimmen, welche Terme am stärksten zur Streuung der Antwortvariablen beitragen

Verwenden Sie ein Pareto-Diagramm, um die relative Größe und die statistische Signifikanz von Haupt- und Wechselwirkungseffekten zu vergleichen. Im Diagramm wird der Typ des Effekts wie folgt dargestellt:

Wenn das Modell keinen Fehlerterm enthält, werden im Diagramm die Absolutwerte der nicht standardisierten Effekte angezeigt.
Wenn das Modell einen Fehlerterm enthält, werden im Diagramm die Absolutwerte der standardisierten Effekte angezeigt.

Minitab stellt die Effekte in absteigender Reihenfolge ihrer Absolutwerte dar. Die Referenzlinie im Diagramm zeigt, welche Effekte signifikant sind. In der Standardeinstellung zeichnet Minitab die Referenzlinie bei einem Signifikanzniveau von 0,05. Wenn kein Fehlerterm vorhanden ist, zeichnet Minitab die Referenzlinie mit Hilfe der Lenth-Methode.

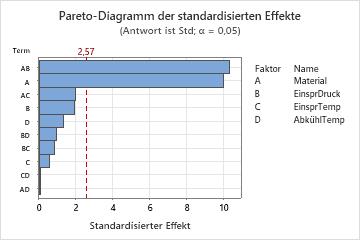
In diesem Diagramm sind der Haupteffekt für „Material“ und die Wechselwirkung zwischen „Material“ und „EinsprDruck“ signifikant (α = 0,05).

Schritt 2: Bestimmen, welche Terme statistisch signifikante Effekte auf die Antwortvariable haben

Um zu bestimmen, ob die Assoziation zwischen der Antwortvariablen und jedem Term im Modell statistisch signifikant ist, vergleichen Sie den p-Wert für den Term mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese besagt, dass der Koeffizient des Terms gleich null ist, was bedeutet, dass keine Assoziation zwischen dem Term und der Antwortvariablen besteht. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko, dass auf eine vorhandene Assoziation geschlossen wird, während tatsächlich keine vorhanden ist, von 5 %.

p-Wert ≤ α: Die Assoziation ist statistisch signifikant: Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht.
p-Wert > α: Die Assoziation ist statistisch nicht signifikant: Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht. Es empfiehlt sich möglicherweise, dass Modell ohne den Term erneut anzupassen.; Wenn mehrere Prädiktoren ohne eine statistisch signifikante Assoziation mit der Antwortvariablen vorhanden sind, können Sie das Modell reduzieren, indem Sie Terme einzeln nacheinander entfernen. Weitere Informationen zum Entfernen von Termen aus dem Modell finden Sie unter Modellreduzierung.

Wenn ein Modellterm statistisch signifikant ist, hängt die Interpretation von der Art des Terms ab. Die Interpretationen lauten wie folgt:

Wenn ein Koeffizient für einen Faktor signifikant ist, können Sie schlussfolgern, dass nicht alle Standardabweichungen der einzelnen Stufen gleich sind.
Wenn ein Koeffizient für eine Kovariate signifikant ist, besteht eine Assoziation zwischen Änderungen des Werts der Variablen und Änderungen der Standardabweichung der Antwortvariablen.
Wenn ein Koeffizient für einen Wechselwirkungsterm signifikant ist, hängt die Beziehung zwischen einem Faktor und der Antwortvariablen von den anderen Faktoren im Term ab. In diesem Fall sollten Sie die Haupteffekte nicht interpretieren, ohne dabei den Wechselwirkungseffekt zu berücksichtigen.

Kodierte Koeffizienten für Ln(Std)

Term	Effekt	Verhältniseffekt	Koef	SE Koef	t-Wert	p-Wert	VIF
Konstante			0,3424	0,0481	7,12	0,001
Material	-0,9598	0,3830	-0,4799	0,0481	-9,99	0,000	1,00
EinsprDruck	-0,1845	0,8315	-0,0922	0,0481	-1,92	0,113	1,00
EinsprTemp	0,0555	1,0571	0,0278	0,0481	0,58	0,589	1,00
AbkühlTemp	-0,1259	0,8817	-0,0629	0,0481	-1,31	0,247	1,00
Material*EinsprDruck	-0,9918	0,3709	-0,4959	0,0481	-10,32	0,000	1,00
Material*EinsprTemp	0,1875	1,2062	0,0937	0,0481	1,95	0,109	1,00
Material*AbkühlTemp	0,0056	1,0056	0,0028	0,0481	0,06	0,956	1,00
EinsprDruck*EinsprTemp	-0,0792	0,9239	-0,0396	0,0481	-0,82	0,448	1,00
EinsprDruck*AbkühlTemp	-0,0900	0,9139	-0,0450	0,0481	-0,94	0,392	1,00
EinsprTemp*AbkühlTemp	0,0066	1,0066	0,0033	0,0481	0,07	0,948	1,00

Wichtigste Ergebnisse: p-Wert, Koeffizienten

In diesen Ergebnissen sind der Haupteffekt für „Material“ und die Wechselwirkung zwischen „Material“ und „EinsprDruck“ signifikant (α = 0,05). Sie können schlussfolgern, dass zwischen Änderungen dieser Variablen und Änderungen der Antwortvariablen eine Assoziation besteht.

Schritt 3: Bestimmen, wie gut das Modell an die Daten angepasst ist

Um zu ermitteln, wie gut das Modell an die Daten angepasst ist, untersuchen Sie die Statistiken für die Güte der Anpassung in der Tabelle „Zusammenfassung des Modells“.

Hinweis

Bei der Verwendung der Maximum-Likelihood-Schätzmethode wird die Tabelle „Zusammenfassung des Modells“ nicht angezeigt.

S

Verwenden Sie S, um zu ermitteln, wie genau das Modell die Antwortvariable beschreibt. Verwenden Sie S anstelle von R², um die Anpassung von Modellen zu vergleichen, die keine Konstante enthalten.

S wird in der Maßeinheit der Antwortvariablen ausgedrückt und stellt den Abstand der Datenwerte von den angepassten Werten dar. Je niedriger der Wert von S, desto genauer beschreibt das Modell die Antwortvariable. Ein niedriger Wert von S allein bedeutet jedoch nicht zwangsläufig, dass das Modell die Modellannahmen erfüllt. Prüfen Sie die Annahmen anhand der Residuendiagramme.

R-Qd

Je höher das R2, desto besser ist das Modell an die Daten angepasst. Das R² liegt immer zwischen 0 % und 100 %.

Der Wert von R² nimmt beim Einbinden zusätzlicher Prädiktoren in das Modell stets zu. Das beste Modell mit fünf Prädiktoren weist beispielsweise immer ein R² auf, das mindestens so hoch wie das des besten Modells mit vier Prädiktoren ist. Daher ist R² am nützlichsten, wenn Sie Modelle derselben Größe vergleichen.

R-Qd(kor)

Verwenden Sie das korrigierte R², wenn Sie Modelle vergleichen möchten, die eine unterschiedliche Anzahl von Prädiktoren enthalten. R² nimmt stets zu, wenn Sie einen zusätzlichen Prädiktor in das Modell aufnehmen, selbst wenn damit keine tatsächliche Verbesserung des Modells verbunden ist. Der Wert des korrigierten R² berücksichtigt die Anzahl der Prädiktoren im Modell, so dass Ihnen das Auswählen des richtigen Modells erleichtert wird.

R-Qd(prog)

Verwenden Sie das prognostizierte R2, um zu ermitteln, wie genau das Modell Werte der Antwortvariablen für neue Beobachtungen prognostiziert. Modelle mit einem höheren prognostizierten R² zeichnen sich durch eine bessere Prognosefähigkeit aus.

Ein prognostiziertes R², das wesentlich kleiner als R² ist, kann auf eine übermäßige Anpassung des Modells hinweisen. Ein übermäßig angepasstes Modell liegt vor, wenn Sie Terme für Effekte hinzufügen, die in der Grundgesamtheit unbedeutend sind. Das Modell wird somit an die Stichprobendaten angepasst und ist daher möglicherweise beim Aufstellen von Prognosen für die Grundgesamtheit nicht nützlich.

Das prognostizierte R² kann zudem beim Vergleichen von Modellen nützlicher als das korrigierte R² sein, da der Wert mit Beobachtungen berechnet wird, die in der Modellberechnung nicht enthalten sind.

AICc und BIC

Wenn Sie die Details für die einzelnen Schritte einer Methode der schrittweisen Regression oder die erweiterten Ergebnisse der Analyse abrufen, zeigt Minitab zwei weitere Statistiken an. Bei diesen Statistiken handelt es sich um Akaikes korrigiertes Informationskriterium (AICc) und das Bayessche Informationskriterium (BIC). Anhand dieser Statistiken können Sie verschiedene Modelle vergleichen. Bei jeder dieser Statistiken sind kleinere Werte erwünscht.

Berücksichtigen Sie die folgenden Punkte, wenn Sie die Statistiken für die Güte der Anpassung interpretieren:

Kleine Stichproben ermöglichen keinen genauen Schätzwert für die Stärke der Beziehung zwischen der Antwortvariablen und den Prädiktoren. Wenn z. B. das R² genauer sein muss, sollten Sie einen größeren Stichprobenumfang (im Allgemeinen 40 oder mehr) wählen.
Statistiken für die Güte der Anpassung sind nur eines der Maße für die Güte der Anpassung des Modells an die Daten. Selbst wenn ein Modell einen erwünschten Wert aufweist, sollten Sie die Residuendiagramme untersuchen, um sich zu vergewissern, dass das Modell die Modellannahmen erfüllt.

Zusammenfassung des Modells für Ln(Std)

S	R-Qd	R-Qd(kor)	R-Qd(prog)
0,549040	97,75%	93,25%	76,97%

Wichtigste Ergebnisse: S, R-Qd, R-Qd(kor), R-Qd(prog)

In diesen Ergebnissen erklärt das Modell 97,75 % der Streuung in der Ausgabe. Für diese Daten gibt das R² an, dass das Modell gut an die Daten angepasst ist. Wenn weitere Modelle mit anderen Prädiktoren angepasst werden, verwenden Sie die Werte des korrigierten R² und des prognostizierten R², um die Güte der Anpassung der Modelle an die Daten zu vergleichen.

Schritt 4: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt

Verwenden Sie die Residuendiagramme, um zu ermitteln, ob das Modell angemessen ist und die Annahmen der Analyse erfüllt. Wenn die Annahmen nicht erfüllt werden, ist das Modell u. U. nicht gut an die Daten angepasst, und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein.

Weitere Informationen zum Umgang mit Mustern in den Residuendiagrammen finden Sie unter Residuendiagramme für Faktoriellen Versuchsplan analysieren; klicken Sie dort auf den Namen des Residuendiagramms in der Liste am oberen Rand der Seite.

Diagramm der Residuen im Vergleich zu den Anpassungen

Die Muster in der folgenden Tabelle können darauf hinweisen, dass das Modell die Modellannahmen nicht erfüllt.

Muster	Mögliche Bedeutung des Musters
Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte	Nicht konstante Varianz
Krümmung	Ein fehlender Term höherer Ordnung
Ein weit von null entfernt liegender Punkt	Ein Ausreißer
Ein in x-Richtung weit von den anderen Punkten entfernter Punkt	Ein einflussreicher Punkt

Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.

Diagramm der Residuen im Vergleich zur Reihenfolge

Verwenden Sie das Diagramm der Residuen im Vergleich zur Reihenfolge, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind. Bei in chronologischer Reihenfolge angezeigten unabhängigen Residuen sind weder Trends noch Muster zu erkennen. Muster in den Punkten können darauf hinweisen, dass nahe beieinander liegende Residuen korrelieren und daher nicht unabhängig sind. Im Idealfall sollten die Residuen im Diagramm zufällig um die Mittellinie gestreut sein: