In diesem Thema
Anpassung
Angepasste Werte sind auch bekannt als Anpassungen oder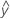 
. Die angepassten Werte sind Punktschätzungen der Standardabweichung der Antwortvariablen für die gegebenen Werte der Prädiktoren. Die Werte der Prädiktoren werden auch als x-Werte bezeichnet.
Interpretation
Angepasste Werte werden durch Einsetzen der spezifischen x-Werte für jede Beobachtung im Datensatz in die Modellgleichung berechnet.
Wenn die Gleichung beispielsweise ln(y) = ln(5 + 10x) lautet, ergibt ein x-Wert von 2 den angepassten Wert 3,21888 (ln(5 + 10(2))).
Beobachtungen mit angepassten Werten, die stark vom beobachteten Wert abweichen, können ungewöhnlich sein. Beobachtungen mit ungewöhnlichen Prädiktorwerten üben möglicherweise einen starken Einfluss aus. Wenn Minitab feststellt, dass Ihre Daten ungewöhnliche oder einflussreiche Werte enthalten, enthält die Ausgabe die Tabelle „Anpassungen und Bewertung für ungewöhnliche Beobachtungen“, in der die betreffenden Beobachtungen identifiziert werden. Die Beobachtungen mit großen standardisierten Residuen werden durch die vorgeschlagene Regressionsgleichung nicht gut modelliert. Es ist jedoch zu erwarten, dass einige ungewöhnliche Beobachtungen vorliegen. Entsprechend den Kriterien für große standardisierte Residuen ist beispielsweise zu erwarten, dass ca. 5 % der Beobachtungen als Beobachtungen mit einem großen standardisierten Residuum gekennzeichnet werden. Weitere Informationen zu ungewöhnlichen Werten finden Sie unter Ungewöhnliche Beobachtungen.
Konfidenzintervall für ursprüngliche Antwortvariable (95%-KI)
Diese Konfidenzintervalle (KI) sind Bereiche von Werten, die wahrscheinlich die Standardabweichung der Antwortvariablen für die Grundgesamtheit enthalten, die die beobachteten Werte der Prädiktoren bzw. Faktoren im Modell aufweist.
Da die Stichproben zufällig sind, ist es unwahrscheinlich, dass zwei Stichproben aus einer Grundgesamtheit identische Konfidenzintervalle ergeben. Wenn Sie die Stichprobennahme jedoch viele Male wiederholen, enthält ein gewisser Prozentsatz der resultierenden Konfidenzintervalle den unbekannten Parameter der Grundgesamtheit. Der Prozentsatz dieser Konfidenzintervalle, die den Parameter enthalten, stellt das Konfidenzniveau des Intervalls dar.
- Punktschätzung
- Die Punktschätzung wird auf der Grundlage der Stichprobendaten berechnet.
- Fehlerspanne
- Die Fehlerspanne definiert die Breite des Konfidenzintervalls, und sie wird durch die beobachtete Streuung in der Stichprobe, den Stichprobenumfang und das Konfidenzniveau bestimmt.
Interpretation
Verwenden Sie das Konfidenzintervall, um den Schätzwert des angepassten Werts für die beobachteten Werte der Variablen auszuwerten.
Bei einem 95%-Konfidenzniveau können Sie sich beispielsweise zu 95 % sicher sein, dass das Konfidenzintervall die Standardabweichung der Grundgesamtheit für die angegebenen Werte der Prädiktorvariablen oder Faktoren im Modell enthält. Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind. Ein breites Konfidenzintervall deutet darauf hin, dass Sie sich bezüglich der Standardabweichung von künftigen Werten weniger sicher sein können. Wenn das Intervall zu breit und damit nicht hilfreich ist, erwägen Sie, den Stichprobenumfang zu vergrößern.
Verhältnisresiduum
Das Verhältnisresiduum ist die beobachtete Standardabweichung dividiert durch den angepassten Wert.
Ln(Std)
Der natürliche Logarithmus der beobachteten Standardabweichung der Antwortvariablen.
Ln (Anpassung)
Der natürliche Logarithmus der angepassten Standardabweichung.
SE Ln(Anpassung)
Der Standardfehler des natürlichen Logarithmus der angepassten Standardabweichung ist ein Schätzwert der Streuung in der geschätzten Standardabweichung für die angegebenen Variableneinstellungen. Der Standardfehler der Anpassung wird bei der Berechnung des Konfidenzintervalls für den Mittelwert der Antwortvariablen verwendet. Standardfehler sind immer nicht negativ.
Interpretation
Verwenden Sie den Standardfehler der Anpassung, um die Genauigkeit des Schätzwerts für den natürlichen Logarithmus der Standardabweichung zu bestimmen. Je kleiner der Standardfehler, desto genauer ist der Schätzwert.
Konfidenzintervall für transformierte Antwortvariable (95%-KI)
Diese Konfidenzintervalle (KI) sind Bereiche von Werten, die wahrscheinlich den natürlichen Logarithmus der Standardabweichung für die Grundgesamtheit enthalten, die die beobachteten Werte der Prädiktoren bzw. Faktoren im Modell aufweist.
Da die Stichproben zufällig sind, ist es unwahrscheinlich, dass zwei Stichproben aus einer Grundgesamtheit identische Konfidenzintervalle ergeben. Wenn Sie die Stichprobennahme jedoch viele Male wiederholen, enthält ein gewisser Prozentsatz der resultierenden Konfidenzintervalle den unbekannten Parameter der Grundgesamtheit. Der Prozentsatz dieser Konfidenzintervalle, die den Parameter enthalten, stellt das Konfidenzniveau des Intervalls dar.
- Punktschätzung
- Die Punktschätzung wird auf der Grundlage der Stichprobendaten berechnet.
- Fehlerspanne
- Die Fehlerspanne definiert die Breite des Konfidenzintervalls, und sie wird durch die beobachtete Streuung in der Stichprobe, den Stichprobenumfang und das Konfidenzniveau bestimmt.
Interpretation
Verwenden Sie das Konfidenzintervall, um den Schätzwert des angepassten Werts für die beobachteten Werte der Variablen auszuwerten.
Bei einem 95%-Konfidenzniveau können Sie sich beispielsweise zu 95 % sicher sein, dass das Konfidenzintervall den Logarithmus der Standardabweichung der Grundgesamtheit für die angegebenen Werte der Prädiktorvariablen oder Faktoren im Modell enthält. Anhand des Konfidenzintervalls können Sie die praktische Signifikanz Ihrer Ergebnisse beurteilen. Bestimmen Sie anhand Ihrer Fachkenntnisse, ob das Konfidenzintervall Werte umfasst, die in der jeweiligen Situation von praktischer Signifikanz sind. Ein breites Konfidenzintervall deutet darauf hin, dass Sie sich bezüglich der Standardabweichung von künftigen Werten weniger sicher sein können. Wenn das Intervall zu breit und damit nicht hilfreich ist, erwägen Sie, den Stichprobenumfang zu vergrößern.
Ln(Residuum)
Hierbei handelt es sich um die Differenz zwischen dem natürlichen Logarithmus der beobachteten Standardabweichung der Antwortvariablen und dem natürlichen Logarithmus der angepassten Standardabweichung. Dies ist der Logarithmus des Verhältnisresiduums.
Interpretation
Das logarithmierte Residuum stellt den Teil der beobachteten Antwortvariablen dar, der nicht durch das Modell erklärt wird. Von den Arten der Residuen, die Minitab in der Funktion Streuung analysieren berechnet, ähneln die logarithmierten Residuen am meisten den regulären Residuen.
Std Ln(Resid)
Das standardisierte Residuum für den natürlichen Logarithmus ist das logarithmierte Residuum dividiert durch dessen (asymptotischen) Standardfehler.
Interpretation
Verwenden Sie die standardisierten Residuen für den natürlichen Logarithmus, um Ausreißer zu erkennen. Wenn die Werte für „Std Ln(Resid)“ zwischen –2 und 2 liegen, weisen die Daten keine ungewöhnlichen Beobachtungen auf.
Standardisierte Residuen größer als 2 bzw. kleiner als −2 werden im Allgemeinen als groß erachtet. Die von Minitab gekennzeichneten Beobachtungen werden durch die vorgeschlagene Regressionsgleichung nicht gut modelliert. Es ist jedoch zu erwarten, dass einige ungewöhnliche Beobachtungen vorliegen. Entsprechend den Kriterien für große standardisierte Residuen ist beispielsweise zu erwarten, dass ca. 5 % der Beobachtungen als Beobachtungen mit einem großen standardisierten Residuum gekennzeichnet werden. Weitere Informationen finden Sie unter Ungewöhnliche Beobachtungen.
Standardisierte Residuen sind hilfreich, da Rohresiduen u. U. keine geeigneten Anzeichen für Ausreißer darstellen. Die Varianz jedes Rohresiduums kann um die mit ihm verbundenen x-Werte abweichen. Diese ungleiche Streuung erschwert es, die Größen der Rohresiduen zu beurteilen. Durch das Standardisieren der Residuen wird dieses Problem behoben, indem die unterschiedlichen Varianzen in eine gemeinsame Skala konvertiert werden.
Hoch (Hebelwirkung)
„Hoch“ (auch als Hebelwirkung bezeichnet) ist ein Maß für den Abstand vom x-Wert einer Beobachtung zum Durchschnitt der x-Werte aller Beobachtungen in einem Datensatz.
Interpretation
Hoch-Werte liegen zwischen 0 und 1. Minitab kennzeichnet Beobachtungen mit Hebelwirkungswerten von mehr als 3p/n oder, falls kleiner, 0,99 in der Tabelle „Anpassungen und Bewertung für ungewöhnliche Beobachtungen“ mit einem „X“. Im Ausdruck 3p/n ist p die Anzahl der Koeffizienten im Modell und n die Anzahl der Beobachtungen. Die von Minitab mit einem „X“ gekennzeichneten Beobachtungen können einflussreich sein.
Beobachtungen mit großem Einfluss wirken sich disproportional auf das Modell aus und können irreführende Ergebnisse verursachen. Das Einbinden oder Ausschließen eines einflussreichen Punkts könnte beispielsweise ändern, ob ein Koeffizient statistisch signifikant ist. Beobachtungen mit großem Einfluss können Hebelwirkungspunkte, Ausreißer oder beides sein.
Wenn Sie eine einflussreiche Beobachtung feststellen, ermitteln Sie, ob es sich bei der Beobachtung um einen Dateneingabe- oder Messfehler handelt. Wenn die Beobachtung weder einen Dateneingabefehler noch einen Messfehler darstellt, bestimmen Sie, wie einflussreich die Beobachtung ist. Passen Sie das Modell zuerst mit der Beobachtung und dann ohne die Beobachtung an. Vergleichen Sie anschließend die Koeffizienten, p-Werte, R2-Werte und weitere Modellinformationen. Wenn sich das Modell nach Entfernen der einflussreichen Beobachtung signifikant ändert, untersuchen Sie das Modell eingehender, um festzustellen, ob Sie das Modell falsch angegeben haben. Möglicherweise müssen Sie weitere Daten erfassen, um das Problem zu beheben.
Cook-Distanz (D)
Die Cook-Distanz (D) ist ein Maß für den Effekt einer Beobachtung auf eine Gruppe von Koeffizienten in einem linearen Modell. Bei der Cook-Distanz werden sowohl die Hebelwirkung als auch das standardisierte Residuum jeder Beobachtung berücksichtigt, um den Effekt der betreffenden Beobachtung zu ermitteln.
Interpretation
Beobachtungen mit einem großen D-Wert können einflussreich sein. Ein D-Wert wird häufig als groß betrachtet, wenn er größer als der Median der F-Verteilung F(0,5; p; n–p) ist, wobei p die Anzahl der Modellterme einschließlich der Konstanten und n die Anzahl der Beobachtungen ist. Sie können die D-Werte auch untersuchen, indem Sie sie in einer Grafik vergleichen, beispielsweise in einem Einzelwertdiagramm. Beobachtungen, deren D-Werte im Verhältnis zu denen anderer Beobachtungen groß sind, können einen starken Einfluss ausüben.
Beobachtungen mit großem Einfluss wirken sich disproportional auf das Modell aus und können irreführende Ergebnisse verursachen. Das Einbinden oder Ausschließen eines einflussreichen Punkts könnte beispielsweise ändern, ob ein Koeffizient statistisch signifikant ist. Beobachtungen mit großem Einfluss können Hebelwirkungspunkte, Ausreißer oder beides sein.
Wenn Sie eine einflussreiche Beobachtung feststellen, ermitteln Sie, ob es sich bei der Beobachtung um einen Dateneingabe- oder Messfehler handelt. Wenn die Beobachtung weder einen Dateneingabefehler noch einen Messfehler darstellt, bestimmen Sie, wie einflussreich die Beobachtung ist. Passen Sie das Modell zuerst mit der Beobachtung und dann ohne die Beobachtung an. Vergleichen Sie anschließend die Koeffizienten, p-Werte, R2-Werte und weitere Modellinformationen. Wenn sich das Modell nach Entfernen der einflussreichen Beobachtung signifikant ändert, untersuchen Sie das Modell eingehender, um festzustellen, ob Sie das Modell falsch angegeben haben. Möglicherweise müssen Sie weitere Daten erfassen, um das Problem zu beheben.
DFITS
DFITS ist ein Maß für den Effekt der einzelnen Beobachtungen auf die angepassten Werte in einem linearen Modell. DFITS stellt die annähernde Anzahl der Standardabweichungen dar, um die sich der angepasste Wert ändert, wenn je eine Beobachtung aus dem Datensatz entfernt und das Modell erneut angepasst wird.
Interpretation
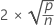
| Begriff | Beschreibung |
|---|---|
| p | Anzahl der Modellterme |
| n | Anzahl der Beobachtungen |
Wenn Sie eine einflussreiche Beobachtung feststellen, ermitteln Sie, ob es sich bei der Beobachtung um einen Dateneingabe- oder Messfehler handelt. Wenn die Beobachtung weder einen Dateneingabefehler noch einen Messfehler darstellt, ermitteln Sie, wie einflussreich die Beobachtung ist. Passen Sie das Modell zuerst mit der Beobachtung und dann ohne die Beobachtung an. Vergleichen Sie anschließend die Koeffizienten, p-Werte, R2-Werte und weitere Modellinformationen. Wenn sich das Modell nach Entfernen der einflussreichen Beobachtung signifikant ändert, untersuchen Sie das Modell eingehender, um festzustellen, ob Sie das Modell falsch angegeben haben. Möglicherweise müssen Sie weitere Daten erfassen, um das Problem zu beheben.
