Methoden und Formeln für die Modellinformationen in Faktoriellen Versuchsplan analysieren

In diesem Thema

Versuchsplanmatrix
Effekte
Koeffizienten (Koef)
Box-Cox-Transformation
Gewichtete Regression

Versuchsplanmatrix

Minitab verfolgt für die Versuchsplanmatrix denselben Ansatz wie im allgemeinen linearen Modell (GLM), bei dem das angegebene Modell mit einer Regression angepasst wird. Zunächst erstellt Minitab auf der Grundlage der Faktoren und des angegebenen Modells eine Versuchsplanmatrix. Die Spalten dieser Matrix (mit X bezeichnet) stellen die Terme im Modell dar.

Die Versuchsplanmatrix enthält n Zeilen, wobei n die Anzahl der Beobachtungen ist, und Spalten, die den Termen im Modell entsprechen. Die Spalten für die Terme weisen in der Versuchsplanmatrix die folgende Reihenfolge auf:

Konstante
Kovariaten
Blöcke
Faktoren
Wechselwirkungen

Diese Typen von Termen verfügen über je eine Spalte in der Versuchsplanmatrix:

Konstante
Kovariate
Stetiger Faktor

Für Blöcke ist die Anzahl der Spalten gleich eins weniger als die Anzahl der Blöcke.

Kategoriale Faktoren und Wechselwirkungen in zweistufigen Versuchsplänen

In einem zweistufigen Versuchsplan weist der Term für einen kategorialen Faktor eine Spalte auf. Jeder Wechselwirkungsterm weist ebenfalls eine Spalte auf.

Kategoriale Faktoren in allgemeinen faktoriellen Versuchsplänen

In einem allgemeinen faktoriellen Versuchsplan können kategoriale Faktoren mehrere Spalten aufweisen. Die Anzahl der Spalten ist gleich der Anzahl der Stufen minus 1. Angenommen, A ist ein Faktor mit vier Stufen. Der Faktor weist folglich drei Freiheitsgrade auf, und sein Block enthält drei Spalten. Angenommen, diese Spalten sind A1, A2 und A3. Jede Zeile ist wie folgt kodiert:

Stufe von A	A1	A2	A3
1	1	0	0
2	0	1	0
3	0	0	1
4	-1	-1	-1

Wechselwirkungen in allgemeinen faktoriellen Versuchsplänen

Um die Spalten für einen Wechselwirkungsterm zu berechnen, werden die entsprechenden Spalten für die Faktoren in der Wechselwirkung multipliziert. Angenommen, Faktor A weist sechs Stufen, Faktor C drei Stufen und Faktor D vier Stufen auf. Der Term A * C * D weist dann 5 x 2 x 3 = 30 Spalten auf. Um die Stufen zu erhalten, wird jede Spalte für A mit jeder für C und jeder für D multipliziert.

Haupteinheitenspalten in Split-Plot-Designs

Hinweis

Minitab analysiert keine Split-Plot-Designs mit einer binären Antwortvariablen.

Für ein Split-Plot-Design verwendet Minitab zwei Versionen der Versuchsplanmatrix. Eine Version ist dieselbe Matrix, die auch für zweistufige faktorielle Versuchspläne verwendet wird. Die andere Matrix enthält einen Block von Spalten, die Haupteinheiten darstellen. Bei der Berechnung des Haupteinheiten-Fehlerterms wird beispielsweise diese zweite Version der Versuchsplanmatrix verwendet. Die Spalten für die Haupteinheiten folgen den Spalten für die schwer veränderbaren Faktoren und Wechselwirkungen, die ausschließlich schwer veränderbare Faktoren umfassen.

Effekte

Geschätzte Effekte für jeden Faktor. Effekte werden nur für zweistufige Modelle und nicht für allgemeine faktorielle Modelle berechnet. Die Formel für den Effekt eines Faktors lautet wie folgt:

Effekt = Koeffizient * 2

Koeffizienten (Koef)

Die Schätzwerte der Regressionskoeffizienten der Grundgesamtheit in einer Regressionsgleichung. Für jeden Faktor berechnet Minitab k – 1 Koeffizienten, wobei k der Anzahl der Stufen im Faktor entspricht. Für ein zweistufiges vollfaktorielles Zwei-Faktor-Modell lauten die Formeln für die Koeffizienten der Faktoren und Wechselwirkungen wie folgt:

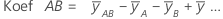
Der Standardfehler des Koeffizienten für dieses zweistufige, vollfaktorielle Zwei-Faktor-Modell wird wie folgt ausgedrückt:

Weitere Informationen zu Modellen mit mehr als zwei Faktoren oder Faktoren mit mehr als zwei Stufen finden Sie in Montgomery¹.

Notation

Begriff	Beschreibung
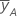	Mittelwert von y auf der hohen Stufe von Faktor A
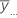	Gesamtmittelwert aller Beobachtungen
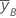	Mittelwert von y auf der hohen Stufe von Faktor B
	Mittelwert von y auf den hohen Stufen von A und B
MSE	mittleres Fehlerquadrat (MSE)
n	Anzahl der Werte –1 und 1 (in der Kovarianzmatrix) für den geschätzten Term

Box-Cox-Transformation

Bei der Box-Cox-Transformation werden Lambda-Werte (siehe unten) ausgewählt, die die Summe der Quadrate der Residuen minimieren. Die resultierende Transformation ist Y ^λ, wenn λ ≠ 0, und ln(Y), wenn λ = 0. Wenn λ < 0, multipliziert Minitab zudem die transformierte Antwortvariable mit −1, um die Reihenfolge aus der nicht transformierten Antwortvariablen beizubehalten.

Minitab sucht einen optimalen Wert zwischen −2 und 2. Werte, die außerhalb dieses Intervalls liegen, führen möglicherweise nicht zu einer besseren Anpassung.

Hier finden Sie einige der gängigsten Transformationen, wobei Y′ das transformierte Y der Daten darstellt:

Lambda-Wert (λ)	Transformation
λ = 2	Y′ = Y ²
λ = 0,5	Y′ =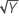
λ = 0	Y′ = ln(Y )
λ = −0,5
λ = −1	Y′ = −1 / Y

Gewichtete Regression

Bei der Regression der gewichteten kleinsten Quadrate handelt es sich um eine Methode zum Behandeln von Beobachtungen, deren Varianzen nicht konstant sind. Wenn die Varianzen nicht konstant sind, gelten für die Beobachtungen folgende Hinweise:

Großen Varianzen sollten relativ kleine Gewichtungen zugewiesen werden.
Kleinen Varianzen sollten relativ große Gewichtungen zugewiesen werden.

Üblicherweise wird für die Gewichtungen die Umkehrung der reinen Fehlervarianz in der Antwortvariablen ausgewählt.

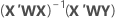
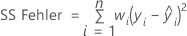
Die Formel für die geschätzten Koeffizienten lautet wie folgt:

Dies entspricht dem Minimieren des gewichteten SS Fehler.

Notation

Begriff	Beschreibung
X	Designmatrix
X'	transponierte Designmatrix
W	eine (n x n)-Matrix mit den Gewichtungen auf der Diagonalen
Y	Vektor von Werten der Antwortvariablen
n	Anzahl der Beobachtungen
w_i	Gewichtung für die i-te Beobachtung
y_i	Wert der Antwortvariablen für die i-te Beobachtung
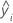	angepasster Wert für die i-te Beobachtung

¹ D. C. Montgomery (1991) Design and Analysis of ExperimentsThird Edition, John Wiley & Sons.