In diesem Thema
Summe der Quadrate (SS)
Die Summe der quadrierten Distanzen. Die angegebenen Formeln beziehen sich auf ein vollfaktorielles Zwei-Faktor-Modell mit den Faktoren A und B. Diese Formeln können für Modelle mit mehr als zwei Faktoren erweitert werden. Weitere Informationen finden Sie in Montgomery1.
„SS Gesamt“ gibt die Gesamtstreuung im Modell an. „SS (A)“ und „SS (B)“ sind die Summe der quadrierten Abweichungen der geschätzten Mittelwerte der Faktorstufen um den Gesamtmittelwert. „SS Fehler“ ist die Summe der quadrierten Residuen. Dies wird auch als Fehler innerhalb von Behandlungen bezeichnet. Die Berechnungen lauten wie folgt:


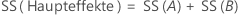
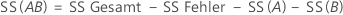






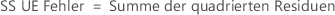
- D. C. Montgomery (1991). Design and Analysis of Experiments, Third Edition, John Wiley & Sons.
Notation
| Begriff | Beschreibung |
|---|---|
| a | Anzahl der Stufen in Faktor A |
| b | Anzahl der Stufen in Faktor B |
| n | Gesamtzahl der Replikationen |
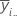 | Mittelwert der i-ten Stufe von Faktor A |
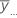 | Gesamtmittelwert aller Beobachtungen |
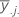 | Mittelwert der j-ten Stufe von Faktor B |
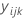 | Beobachtung auf der i-ten Stufe von Faktor A, der j-ten Stufe von Faktor B und in der k-ten Replikation |
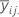 | Mittelwert der i-ten Stufe von Faktor A und der j-ten Stufe von Faktor B |
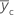 | Mittelwert der Antwortvariablen für Zentralpunkte |
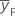 | Mittelwert der Antwortvariablen für Faktorpunkte |
| nF | Anzahl der Faktorpunkte |
Sequenzielle Summe der Quadrate
Minitab schlüsselt die Varianzkomponenten der Summe der Quadrate der Regression bzw. der Behandlungen in sequenzielle Summen der Quadrate für die einzelnen Faktoren auf. Die sequenziellen Summen der Quadrate hängen von der Reihenfolge ab, in der die Faktoren bzw. Prädiktoren in das Modell aufgenommen wurden. Die sequenzielle Summe der Quadrate ist der eindeutige Anteil der Summe der Quadrate der Regression, der durch einen Faktor erklärt wird, nachdem alle zuvor aufgenommenen Faktoren erklärt wurden.
Wenn beispielsweise ein Modell mit den drei Faktoren bzw. Prädiktoren x1, x2 und x3 vorhanden ist, zeigt die sequenzielle Summe der Quadrate für x2, wie viel der verbleibenden Streuung durch x2 erklärt wird, nachdem x1 bereits in das Modell aufgenommen wurde. Wenn Sie eine andere Sequenz der Faktoren erhalten möchten, müssen Sie die Analyse wiederholen und dabei die Faktoren in einer anderen Reihenfolge aufnehmen.
Korrigierte Summe der Quadrate
Die korrigierte Summe der Quadrate hängt nicht von der Reihenfolge ab, in der die Terme in das Modell aufgenommen wurden. Die korrigierte Summe der Quadrate ist der Teil der Streuung, der durch einen Term erklärt wird, sofern alle anderen Terme im Modell enthalten sind, und zwar unabhängig von der Reihenfolge, in der die Terme in das Modell aufgenommen wurden.
Wenn beispielsweise ein Modell mit den drei Faktoren x1, x2 und x3 vorliegt, zeigt die korrigierte Summe der Quadrate für x2, wie viel der verbleibenden Streuung durch den Term für x2 erklärt wird, sofern die Terme für x1 und x3 bereits im Modell enthalten sind.
Die Berechnungen für die korrigierten Summen der Quadrate für drei Faktoren lauten wie folgt:
- SSR(x3 | x1, x2) = SSE (x1, x2) – SSE (x1, x2, x3) oder
- SSR(x3 | x1, x2) = SSR (x1, x2, x3) – SSR (x1, x2)
wobei SSR(x3 | x1, x2) die korrigierte Summe der Quadrate für x3 ist, sofern x1 und x2 im Modell enthalten sind.
- SSR(x2, x3 | x1) = SSE (x1) – SSE (x1, x2, x3) oder
- SSR(x2, x3 | x1) = SSR (x1, x2, x3) – SSR (x1)
wobei SSR(x2, x3 | x1) die korrigierte Summe der Quadrate für x2 und x3 ist, sofern x1 im Modell enthalten ist.
Sie können diese Formeln erweitern, wenn mehr als drei Faktoren im Modell vorhanden sind1.
- J. Neter, W. Wasserman und M. H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Freiheitsgrade (DF)
Für einen vollfaktoriellen Versuchsplan mit den Faktoren A und B und einer Blockvariablen wird die Anzahl der Freiheitsgrade für die einzelnen Summen der Quadrate wie folgt ausgedrückt:







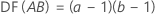

Für zweistufige Versuchspläne mit Zentralpunkten beträgt der Freiheitsgrad für die Krümmung 1.
Notation
| Begriff | Beschreibung |
|---|---|
| a | Anzahl der Stufen in Faktor A |
| b | Anzahl der Stufen in Faktor B |
| c | Anzahl der Blöcke |
| n | Gesamtzahl der Beobachtungen |
| ni | Anzahl der Beobachtungen für die i-te Faktorstufenkombination |
| m | Anzahl der Faktorstufenkombinationen |
| p | Anzahl der Koeffizienten |
Kor MS – Term

F
Ein Test, mit dem bestimmt wird, ob die Wechselwirkungseffekte und die Haupteffekte signifikant sind. Die Formel für die Modellterme lautet wie folgt:

Die Freiheitsgrade für den Test sind:
- Zähler = Freiheitsgrade für Term
- Nenner = Freiheitsgrade für Fehler
Größere Werte von F unterstützen das Zurückweisen der Nullhypothese, dass kein signifikanter Effekt vorhanden ist.
Für balancierte Split-Plot-Designs verwendet die F-Statistik für schwer veränderbare Faktoren das Mittel der Quadrate (MS) für die Fehler der Haupteinheiten im Nenner. Für andere Split-Plot-Designs erstellt Minitab mit einer linearen Kombination der Fehler für die Haupteinheiten (HE) und der Fehler für die Untereinheiten (UE) einen Nenner, dem das erwartete Mittel der Quadrate zugrunde liegt.
p-Wert – Tabelle der Varianzanalyse
Der p-Wert ist ein Wahrscheinlichkeitsmaß, das aus einer F-Verteilung mit den Freiheitsgraden (DF) wie folgt berechnet wird:
- DF des Zählers
- Summe der Freiheitsgrade für den Term oder die Terme im Test
- DF des Nenners
- Freiheitsgrade für Fehler
Formel
1 − P(F ≤ fj)
Notation
| Begriff | Beschreibung |
|---|---|
| P(F ≤ f) | kumulative Verteilungsfunktion für die F-Verteilung |
| f | F-Statistik für den Test |
Test auf fehlende Anpassung für reine Fehler
- Die Summe der quadrierten Abweichungen der Antwortvariablen vom Mittelwert in jeder Gruppe von Replikationen; diese werden addiert, um die Summe der Quadrate für reine Fehler (SS PE) zu erhalten.
- Das Mittel der Quadrate für reine Fehler
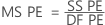

wobei n gleich der Anzahl der Beobachtungen und m gleich der Anzahl der eindeutigen Kombinationen der x-Stufen ist
- Die Summe der Quadrate für fehlende Anpassung
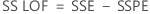
- Das Mittel der Quadrate für fehlende Anpassung

- Die Teststatistik

Große F-Werte und kleine p-Werte weisen darauf hin, dass das Modell ungeeignet ist.
p-Wert – Test auf fehlende Anpassung
- DF des Zählers
- Freiheitsgrade für fehlende Anpassung
- DF des Nenners
- Freiheitsgrade für reine Fehler
Formel
1 − P(F ≤ fj)
Notation
| Begriff | Beschreibung |
|---|---|
| P(F ≤ fj) | kumulative Verteilungsfunktion für die F-Verteilung |
| fj | F-Statistik für den Test |
