Ein Materialtechniker eines Baumaterialherstellers entwickelt ein neues Dämmstoffprodukt. Der Techniker entwirft ein zweistufiges vollfaktorielles Experiment, um verschiedene Faktoren zu untersuchen, die sich möglicherweise auf Festigkeit, Dichte und Dämmwert des Dämmstoffs auswirken.
Der Techniker analysiert einen faktoriellen Versuchsplan, um zu ermitteln, wie sich Materialart, Einspritzdruck, Einspritztemperatur und Abkühltemperatur auf die Festigkeit des Dämmstoffs auswirken.
- Öffnen Sie die Beispieldaten Isolierungseigenschaften.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antworten die Spalte Festigkeit ein.
- Klicken Sie auf Terme.
- Wählen Sie unter Terme in Modell einbinden bis zur Ordnung den Wert 2 aus.
- Klicken Sie auf OK und dann auf Kovariaten.
- Geben Sie im Feld Kovariaten die Spalte MessTemp ein.
- Klicken Sie auf OK und dann auf Grafiken.
- Wählen Sie unter Residuendiagramme die Option Vier-in-eins aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
In der Tabelle der Varianzanalyse sind die p-Werte für alle linearen Terme („Material“, „EinsprDruck“, „EinsprTemp“ und „AbkühlTemp“) signifikant. Da die p-Werte kleiner als das Signifikanzniveau 0,05 sind, schlussfolgert der Techniker, dass die Effekte statistisch signifikant sind. Die Kovariate „MessTemp“ ist nicht signifikant (p-Wert = 0,278). Keine der Zwei-Faktor-Wechselwirkungen ist signifikant. Der Techniker kann in Betracht ziehen, das Modell zu reduzieren.
Das R2 gibt an, dass das Modell 98,02 % der Varianz der Festigkeit erklärt; dies weist darauf hin, dass das Modell außerordentlich gut an die Daten angepasst ist.
Die Mehrzahl der VIF-Werte ist klein, was darauf hindeutet, dass die Terme im Modell nicht korrelieren. Der VIF-Wert für „MessTemp“ ist gleich 5,87, jedoch ist dieser Term nicht signifikant, und Sie würden ihn nicht in das endgültige Modell einbinden.
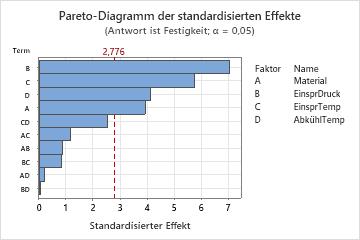
Mit Hilfe des Pareto-Diagramms der Effekte können Sie die wichtigen Effekte in einer grafischen Darstellung identifizieren und die relative Größe der verschiedenen Effekte miteinander vergleichen. Dabei hat der Einspritzdruck (B) den größten Effekt, da der entsprechende Balken am längsten ist. Der Effekt der Wechselwirkung zwischen Einspritzdruck und Abkühltemperatur (BD) ist am geringsten, da der entsprechende Balken der kürzeste ist.
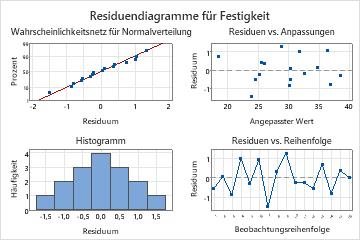
Die Residuendiagramme weisen nicht auf Probleme mit dem Modell hin.
Kodierte Koeffizienten
| Term | Effekt | Koef | SE Koef | t-Wert | p-Wert | VIF |
|---|---|---|---|---|---|---|
| Konstante | 56,0 | 21,0 | 2,66 | 0,056 | ||
| MessTemp | -1,229 | 0,979 | -1,25 | 0,278 | 5,87 | |
| Material | 5,316 | 2,658 | 0,678 | 3,92 | 0,017 | 3,23 |
| EinsprDruck | 5,645 | 2,822 | 0,401 | 7,04 | 0,002 | 1,13 |
| EinsprTemp | 4,355 | 2,177 | 0,378 | 5,76 | 0,005 | 1,00 |
| AbkühlTemp | -3,457 | -1,729 | 0,420 | -4,12 | 0,015 | 1,24 |
| Material*EinsprDruck | -0,723 | -0,361 | 0,415 | -0,87 | 0,433 | 1,21 |
| Material*EinsprTemp | -1,025 | -0,512 | 0,443 | -1,16 | 0,312 | 1,38 |
| Material*AbkühlTemp | -0,208 | -0,104 | 0,510 | -0,20 | 0,848 | 1,82 |
| EinsprDruck*EinsprTemp | -0,837 | -0,419 | 0,510 | -0,82 | 0,458 | 1,82 |
| EinsprDruck*AbkühlTemp | -0,055 | -0,027 | 0,382 | -0,07 | 0,947 | 1,03 |
| EinsprTemp*AbkühlTemp | 1,933 | 0,966 | 0,381 | 2,54 | 0,064 | 1,02 |
Zusammenfassung des Modells
| S | R-Qd | R-Qd(kor) | R-Qd(prog) |
|---|---|---|---|
| 1,51005 | 98,02% | 92,57% | 70,86% |
Varianzanalyse
| Quelle | DF | Kor SS | Kor MS | F-Wert | p-Wert |
|---|---|---|---|---|---|
| Modell | 11 | 451,357 | 41,032 | 17,99 | 0,007 |
| Kovariaten | 1 | 3,591 | 3,591 | 1,58 | 0,278 |
| MessTemp | 1 | 3,591 | 3,591 | 1,58 | 0,278 |
| Linear | 4 | 304,587 | 76,147 | 33,39 | 0,002 |
| Material | 1 | 35,053 | 35,053 | 15,37 | 0,017 |
| EinsprDruck | 1 | 113,068 | 113,068 | 49,59 | 0,002 |
| EinsprTemp | 1 | 75,533 | 75,533 | 33,12 | 0,005 |
| AbkühlTemp | 1 | 38,666 | 38,666 | 16,96 | 0,015 |
| 2-Faktor-Wechselwirkungen | 6 | 20,309 | 3,385 | 1,48 | 0,366 |
| Material*EinsprDruck | 1 | 1,732 | 1,732 | 0,76 | 0,433 |
| Material*EinsprTemp | 1 | 3,045 | 3,045 | 1,34 | 0,312 |
| Material*AbkühlTemp | 1 | 0,095 | 0,095 | 0,04 | 0,848 |
| EinsprDruck*EinsprTemp | 1 | 1,538 | 1,538 | 0,67 | 0,458 |
| EinsprDruck*AbkühlTemp | 1 | 0,012 | 0,012 | 0,01 | 0,947 |
| EinsprTemp*AbkühlTemp | 1 | 14,694 | 14,694 | 6,44 | 0,064 |
| Fehler | 4 | 9,121 | 2,280 | ||
| Gesamt | 15 | 460,478 |
Regressionsgleichung in nicht kodierten Einheiten
| Festigkeit | = | 52,7 - 1,229 MessTemp + 10,43 Material + 0,216 EinsprDruck + 0,007 EinsprTemp - 1,357 AbkühlTemp - 0,0096 Material*EinsprDruck - 0,0683 Material*EinsprTemp - 0,0104 Material*AbkühlTemp - 0,00149 EinsprDruck*EinsprTemp - 0,00007 EinsprDruck*AbkühlTemp + 0,01288 EinsprTemp*AbkühlTemp |
|---|
Aliasstruktur
| Faktor | Name |
|---|---|
| A | Material |
| B | EinsprDruck |
| C | EinsprTemp |
| D | AbkühlTemp |
| Aliase |
|---|
| I - 5,42 ABC + 28,92 ABD - 9,04 ACD - 10,85 BCD + 45,19 ABCD |
| A + 0,15 ABC - 0,77 ABD + 0,24 ACD + 0,29 BCD - 1,21 ABCD |
| B - 0,03 ABC + 0,19 ABD - 0,06 ACD - 0,07 BCD + 0,29 ABCD |
| C - 0,01 ABC + 0,03 ABD - 0,01 ACD - 0,01 BCD + 0,05 ABCD |
| D - 0,05 ABC + 0,25 ABD - 0,08 ACD - 0,09 BCD + 0,39 ABCD |
| AB + 0,04 ABC - 0,24 ABD + 0,07 ACD + 0,09 BCD - 0,37 ABCD |
| AC + 0,06 ABC - 0,32 ABD + 0,10 ACD + 0,12 BCD - 0,50 ABCD |
| AD - 0,09 ABC + 0,47 ABD - 0,15 ACD - 0,18 BCD + 0,74 ABCD |
| BC + 0,09 ABC - 0,47 ABD + 0,15 ACD + 0,18 BCD - 0,74 ABCD |
| BD + 0,02 ABC - 0,08 ABD + 0,03 ACD + 0,03 BCD - 0,13 ABCD |
| CD - 0,01 ABC + 0,07 ABD - 0,02 ACD - 0,03 BCD + 0,11 ABCD |