- Binäres logistisches Modell anpassen
- Binäre Antwort für definitiven Screening-Versuchsplan analysieren
- Binäre Antwort für faktoriellen Versuchsplan analysieren
- Binäre Antwort für Wirkungsflächenversuchsplan analysieren
In diesem Thema
Residuen nach Pearson
Hierbei handelt es sich um Elemente der Chi-Quadrat-Statistik nach Pearson, mit denen Sie schlecht angepasste Faktoren-/Kovariatenmuster erkennen können. Minitab speichert das Residuum nach Pearson für das i-te Faktoren-/Kovariatenmuster. Die Formel lautet wie folgt:
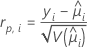
Notation
| Begriff | Beschreibung |
|---|---|
| yi | Wert der Antwortvariablen für das i-te Faktoren-/Kovariatenmuster |
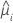 | angepasster Wert für das i-te Faktoren-/Kovariatenmuster |
| V | Varianzfunktion für das Modell bei 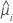 |
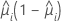
Standardisierte und entfernte Residuen nach Pearson
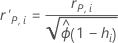
Notation
| Begriff | Beschreibung |
|---|---|
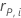 | Residuum nach Pearson für das i-te Faktoren-/Kovariatenmuster |
 | 1, für Binomialmodelle |
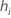 | Hebelwirkung für das i-te Faktoren-/Kovariatenmuster |
Abweichungsresiduen
Abweichungsresiduen basieren auf der Modellabweichung und sind hilfreich, um schlecht angepasste Faktoren-/Kovariatenmuster zu identifizieren. Die Modellabweichung ist eine Statistik zur Güte der Anpassung, die auf der Log-Likelihood-Funktion beruht. Das für das i-te Faktoren-/Kovariatenmuster definierte Abweichungsresiduum ist:

Notation
| Begriff | Beschreibung |
|---|---|
| yi | Wert der Antwortvariablen für das i-te Faktoren-/Kovariatenmuster |
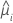 | angepasster Wert für das i-te Faktoren-/Kovariatenmuster |
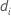 | Abweichung für das i-te Faktoren-/Kovariatenmuster |
Standardisiertes Abweichungsresiduum

Notation
| Begriff | Beschreibung |
|---|---|
| rD,i | Abweichungsresiduum für das i-te Faktoren-/Kovariatenmuster |
| hi | Hebelwirkung für das i-te Faktoren-/Kovariatenmuster |
Gelöschtes Abweichungsresiduum

Notation
| Begriff | Beschreibung |
|---|---|
| yi | Wert der Antwortvariablen beim i-ten Faktoren-/Kovariatenmuster |
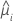 | angepasster Wert für das i-te Faktoren-/Kovariatenmuster |
| hi | Hebelwirkung für das i-te Faktoren-/Kovariatenmuster |
| r'D,i | standardisiertes Abweichungsresiduum für das i-te Faktoren-/Kovariatenmuster |
| r'P,i | standardisiertes Residuum nach Pearson für das i-te Faktoren-/Kovariatenmuster |
1. Pregibon, D. (1981). „Logistic Regression Diagnostics.“ The Annals of Statistics, Vol. 9, No. 4, S. 705–724.
Delta-Chi-Quadrat
Minitab berechnet die Änderung im Chi-Quadrat nach Pearson, die dadurch bedingt ist, dass alle Beobachtungen mit dem j-ten Faktoren-/Kovariatenmuster entfernt wurden. Für jedes eindeutige Faktoren-/Kovariatenmuster in den Daten speichert Minitab einen Delta-Chi-Quadrat-Wert. Mit Hilfe des Delta-Chi-Quadrats können Sie schlecht angepasste Faktoren-/Kovariatenmuster erkennen. Die Formel für das Delta-Chi-Quadrat lautet:
Formel
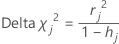
Notation
| Begriff | Beschreibung |
|---|---|
| hj | Hebelwirkung |
| rj | Residuen nach Pearson |
Delta-Abweichung
Minitab berechnet die Änderung in der Abweichungsstatistik, indem alle Beobachtungen mit dem j-ten Faktoren-/Kovariatenmuster entfernt werden. Für jedes eindeutige Faktoren-/Kovariatenmuster in den Daten speichert Minitab einen Wert. Mit Hilfe der Delta-Abweichung können Sie schlecht angepasste Faktoren-/Kovariatenmuster erkennen. Die Änderung in der Abweichungsstatistik lautet:
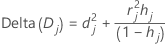
Notation
| Begriff | Beschreibung |
|---|---|
| hj | Hebelwirkung |
| rj | Residuen nach Pearson |
| dj | Abweichungsresiduen |
Delta-Beta (standardisiert)
Minitab berechnet die Änderung, indem alle Beobachtungen mit dem j-ten Faktoren-/Kovariatenmuster entfernt werden. Für jedes eindeutige Faktoren-/Kovariatenmuster in den Daten wird ein Wert gespeichert. Mit Hilfe des standardisierten Delta-β können Faktor-/Kovariatenmuster erkannt werden, die einen starken Einfluss auf die Schätzwerte der Koeffizienten haben. Dieser Wert basiert auf dem standardisierten Residuum nach Pearson.
Formel
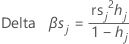
Notation
| Begriff | Beschreibung |
|---|---|
| hj | Hebelwirkung |
| rs j | standardisierte Residuen nach Pearson |
Delta-Beta
Minitab berechnet die Änderung, indem alle Beobachtungen mit dem j-ten Faktoren-/Kovariatenmuster entfernt werden. Für jedes eindeutige Faktoren-/Kovariatenmuster in den Daten wird ein Wert gespeichert. Mit Hilfe des Delta-β können Faktor-/Kovariatenmuster erkannt werden, die einen starken Einfluss auf die Schätzwerte der Koeffizienten haben. Dieser Wert basiert auf dem Residuum nach Pearson.
Formel
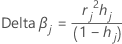
Notation
| Begriff | Beschreibung |
|---|---|
| hj | Hebelwirkung |
| rj | Residuen nach Pearson |
Hebelwirkungen
Die Hebelwirkungen sind die Diagonalelemente der verallgemeinerten „Dach-Matrix“ (Hat-Matrix). Die Hebelwirkungen sind nützlich, um Faktoren-/Kovariatenmuster zu erkennen, die möglicherweise einen signifikanten Einfluss auf die Ergebnisse haben.
Formel
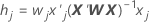
Notation
| Begriff | Beschreibung |
|---|---|
| wj | j-tes Diagonalelement der Gewichtungsmatrix aus der Anpassung der Koeffizienten |
| xj | j-te Zeile der Designmatrix |
| X | Designmatrix |
| X' | transponiertes X |
| W | Gewichtungsmatrix aus der Schätzung der Koeffizienten |
Cook-Distanz
Formel
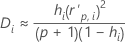
Notation
| Begriff | Beschreibung |
|---|---|
| hi | Hebelwirkung für das i-te Faktoren-/Kovariatenmuster |
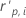 | standardisiertes Residuum nach Pearson für das i-te Faktoren-/Kovariatenmuster |
| p | Freiheitsgrade der Regression |
DFITS
Ein Maß für den Einfluss einer einzelnen Entfernung auf die angepassten Werte. Bei Beobachtungen mit großen DFITS-Werten handelt es sich möglicherweise um Ausreißer. Minitab berechnet einen ungefähren Wert für DFITS.
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| hi | Hebelwirkung für den Datenpunkt |
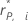 | Das entfernte Residuum nach Pearson für den Datenpunkt |
Varianzinflationsfaktor (VIF)

Notation
| Begriff | Beschreibung |
|---|---|
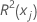 | Determinationskoeffizient mit xj als Antwortvariable und den anderen Termen im Modell als Prädiktoren |
1. P. McCullagh und J. A. Nelder (1989). Generalized Linear Models, 2nd Edition, Chapman & Hall/CRC, London.
