Die Tukey-Methode wird bei der ANOVA verwendet, um Konfidenzintervalle für alle paarweisen Differenzen zwischen Mittelwerten der Faktorstufen zu erstellen, während die simultane Irrtumswahrscheinlichkeit auf einem von Ihnen angegebenen Niveau gehalten wird. Bei Mehrfachvergleichen ist es wichtig, die simultane Irrtumswahrscheinlichkeit zu berücksichtigten, weil die Wahrscheinlichkeit eines Fehlers 1. Art bei einer Serie von Vergleichen größer als die Irrtumswahrscheinlichkeit für einen Vergleich alleine ist. Um dieser höheren Irrtumswahrscheinlichkeit zu begegnen, korrigiert die Tukey-Methode das Konfidenzniveau für jedes einzelne Intervall, so dass das resultierende simultane Konfidenzniveau dem angegebenen Wert entspricht.
Beispiel für Tukey-Konfidenzintervalle
Sie messen die Reaktionszeit von Speicherchips. Ihre Stichprobe umfasst 25 Chips von fünf verschiedenen Herstellern.
Sie untersuchen sämtliche 10 Vergleiche zwischen den fünf Werken, um die abweichenden Mittelwerte genau zu ermitteln. Mit Hilfe der Tukey-Methode geben Sie an, dass die gesamte Gruppe von Vergleichen eine simultane Irrtumswahrscheinlichkeit von 0,05 aufweisen soll (dies entspricht einem simultanen Konfidenzniveau von 95 %). Minitab berechnet, dass die zehn individuellen Konfidenzniveaus den Wert 99,35 % aufweisen müssen, um ein simultanes Konfidenzniveau von 95 % zu erhalten. Diese breiteren Tukey-Konfidenzintervalle bieten weniger präzise Schätzwerte des Parameters der Grundgesamtheit, doch senken sie die Wahrscheinlichkeit, dass mindestens ein Konfidenzintervall die wahre Differenz nicht enthält, auf maximal 5 %. Innerhalb dieses Kontexts können Sie nun ermitteln, ob es Konfidenzintervalle gibt, die den Wert null nicht enthalten, was auf eine signifikante Differenz hinweist.
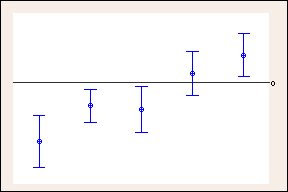
Konfidenzintervalle mit individuellen Konfidenzniveaus von 95 %
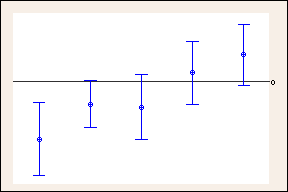
Unter Verwendung der Tukey-Methode berechnete Konfidenzintervalle mit individuellen Konfidenzniveaus von 99,35 %, um ein simultanes Konfidenzniveau von 95 % zu erhalten
Vergleich der 95%-Konfidenzintervalle mit den unter Verwendung des Tukey-Verfahrens berechneten breiteren 99,35%-Konfidenzintervallen im vorherigen Beispiel. Die Referenzlinie bei 0 veranschaulicht, wie die breiteren Tukey-Konfidenzintervalle zu anderen Schlussfolgerungen führen können. Konfidenzintervalle, die null enthalten, weisen darauf hin, dass keine Differenz vorliegt. (Aus Platzgründen werden hier nur 5 der 10 Vergleiche dargestellt.)
